摘要:本文向广大电路设计人员介绍了一种利用Excel电子表对电路进行全面的统计分析的简单方法,几乎适用于任何电路。本文介绍的方法对于深入了解电路在实际环境中的运行情况,确保较高的良率很有帮助。
构建、测试和支持能够在不同电路参数下运行的电路成本较低。
本文阐述了利用容差分析预测良率,即有多少种以不同组件构建的电路能够符合规格要求。为了获得有效的良率分析,必须要拥有:
表1. 良率分析方法
本文将介绍如何使用Microsoft Excel进行良率分析。
我们讨论了概率分布函数等基本的良率分析概念,我们将了解如何按照所要求的概率分布随机生成元件值。
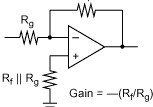
例如,对于图1所示简单的放大电路,已知Rf和Rg电阻后(假设是一个理想的运算放大器),可以很容易地计算出该电路的增益。实际应用中,如果数百次地构建该电路,将会发现每次的Rf和Rg元件值均不同。对该电路进行测试时,每次构建电路的增益也不同。
该电路中,元件值的变化源于电阻的容差。增益计算公式为:增益 = - Rf / Rg。例如,如果取Rf = 1kΩ、Rg = 1kΩ,则增益为-1。
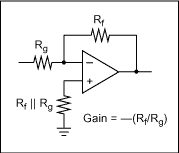
图1. 反相运算放大器示例
最终得到的电路规格可能为:增益 = -1 ± 0.1 V/V。
pdf是表达随机变量X的可能取值x与实际数值出现概率的关系曲线或函数。例如,在我们列举的电路中,可以得出Rf电阻值与一批电阻中出现该电阻值概率的关系。
cdf为累积分布函数,为随机变量X取一个小于或等于某个x值的概率。即如果得到pdf,可以利用积分计算cdf。您可能采用高斯或正态分布的pdf,由两个参数定义:平均值(中心值)和标准方差(约等于峰值宽度)。图2给出了正态分布的pdf和cdf。
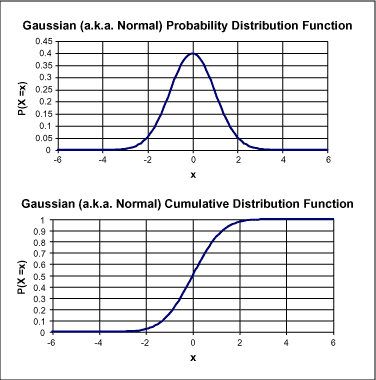
图2. PDF和CDF示例
正态分布与大多数实际情况相吻合,更容易建立数学模型。但是,请务必注意!正态分布可能并不真的代表某种特定情况。例如,如果您正在使用的是20%容差的电阻,可能容差为5%的电阻已全部被筛选出去,并被出售给其他人,您看到的实际pdf如图3所示。
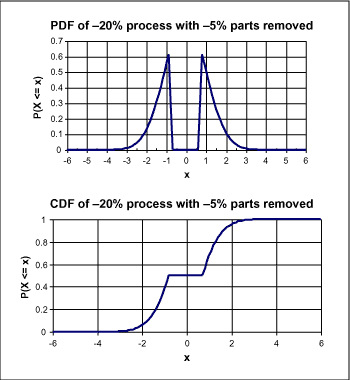
图3. 筛选元件的分布情况
按照这种分布,测量电阻与电阻标签完全相同的概率为零!与使用正态分布的元件电路相比,您的电路所提供的性能会很差。另外,获得5%电阻的用户则会得到比较好的工作特性,因为他们所得到的元件的概率分布函数中已经消除了偏差较大的部分。
由此可见,可供选择的分布函数有许多,而如何选择分布非常重要。因此,不要局限于正态分布这一种。
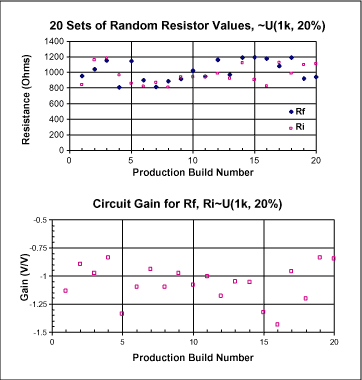
图4. 生成随机电阻值
上述分析中,每个电阻均使用了均匀分布随机变量。这种均匀分布下,取值在两个极限值之间的概率都一样。可以使用两种方法生成电阻值:选择Tools | Data Analysis | Random Number Generation,或使用RAND()函数(请参考RANDBETWEEN() )。如果采用RAND()函数,电子表格每次计算便重新产生一个数值(按F9键)。
不幸的是,大多数元件所遵循的概率分布并非均匀分布。但是,这类分析在估计最差性能时较为快速和有效。
Excel提供了大量其它函数,可以帮助我们生成更为真实的pdf。我们将在下节对其进行介绍,之后叙述利用生产数据生成任意pdf的一些方法。
标准方差(通常称为Σ)描述了pdf函数峰值的宽度,相当于二次求导的极性变化分界点,我们利用该方法生成图2所示pdf。通过将“FALSE”改变为“TRUE”,可以得到cdf值。
如果没有更准确的信息,则假设元件的百分比容差为±3标准方差。例如,±10%的元件会具有±10/3的标准偏差,标称值为±3.33%。
尽管cdf和pdf正确地描述了正态随机变量,但它们不生成随机元件值。理想状态下,我们会倾向于使用类似于“RANDNORM()”的函数,所返回的随机数符合正态分布。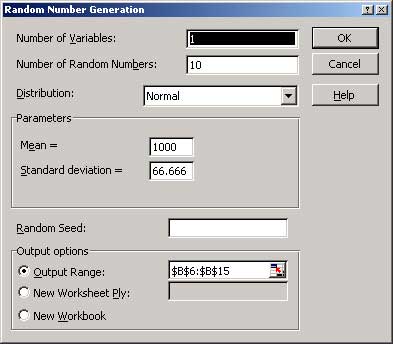
图5. 生成随机数的对话框
注意,我已输入步骤1中计算得到的平均数和标准方差。输入数字10,表示要生成的随机数(值)个数。输入电子表格中要求Excel输出值的位置。输出结果如下:
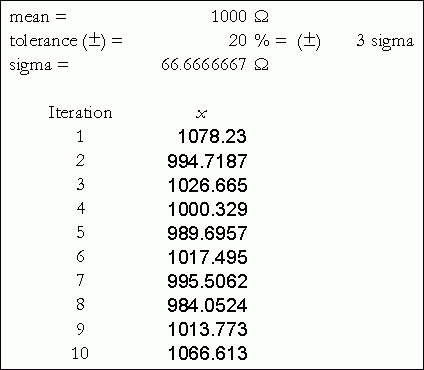
图6. Excel生成的随机元件值
这种情况下,我们会想要描绘一种分布,利用生产测试数据创建一种分布或者使用计算数据创建一种分布,然后生成符合这种分布的随机数,以进行良率分析。
创建此类分布以及符合这种分布的随机数,包括如下几个步骤(如后面图7所示)。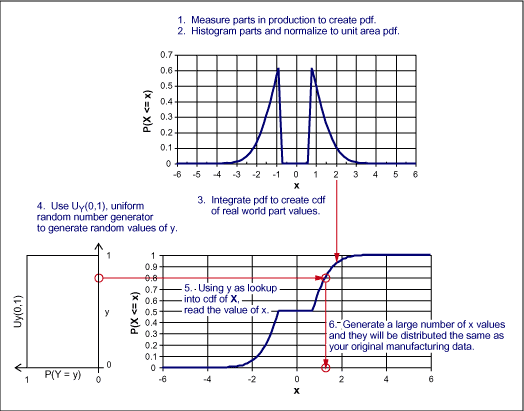
图7. 生成与生产数据一致的随机数
引言
设计在实际环境中运行良好的电路具有一定的挑战性。仅仅以电路设计符合规范为目标还不能满足实际要求,准确预测电路在一定范围工作条件下的运行状况非常重要,包括元件值的实际变化。在深入了解这些运行状况的基础上,设计人员可以有效地选择电路和元件,以达到所要求的制造容限。构建、测试和支持能够在不同电路参数下运行的电路成本较低。
本文阐述了利用容差分析预测良率,即有多少种以不同组件构建的电路能够符合规格要求。为了获得有效的良率分析,必须要拥有:
- 较好的电路模型,包括重要元件、杂散特性等。
- 较好地预计元件值变化的模型
- 合格/不合格的定义或规格
表1. 良率分析方法
| Yield Analysis Tool | Technique | Best used for |
| SPICE | Multiple simulations | Brute force proof circuit will work, awkward for gaining intuition |
| SPICE | SENS sensitivity analysis | Brute force method, good for getting intuition about what components matter |
| Exact closed-form analysis | Using an equation for the circuit performance calculate sensitivities. Using equations for the component variations and the sensitivities calculate the probability of meeting spec | Very simple problems only, gives good insight into technique |
| Microsoft Excel, MathCAD | Create cdfs with manufacturing data, model circuit with | Intermediate complexity, can incorporate real world data, gives good intuition into the problem |
本文将介绍如何使用Microsoft Excel进行良率分析。
我们讨论了概率分布函数等基本的良率分析概念,我们将了解如何按照所要求的概率分布随机生成元件值。
利用元件值和设计公式确定良率
电路由元器件组成。这些元件组装后构成电路,运行状况遵循一定的规则或设计公式。为了进行良率分析,需要了解元件值的变化和设计公式。例如,对于图1所示简单的放大电路,已知Rf和Rg电阻后(假设是一个理想的运算放大器),可以很容易地计算出该电路的增益。实际应用中,如果数百次地构建该电路,将会发现每次的Rf和Rg元件值均不同。对该电路进行测试时,每次构建电路的增益也不同。
该电路中,元件值的变化源于电阻的容差。增益计算公式为:增益 = - Rf / Rg。例如,如果取Rf = 1kΩ、Rg = 1kΩ,则增益为-1。

图1. 反相运算放大器示例
最终得到的电路规格可能为:增益 = -1 ± 0.1 V/V。
元件的PDF和CDF
总之,我们无法提前预测某个元件将会出现的数值。但凭借经验,我们可以预测多数元件的状况,或多数产品的工作情形。可以利用pdf或概率分布函数描述这种状况。pdf是表达随机变量X的可能取值x与实际数值出现概率的关系曲线或函数。例如,在我们列举的电路中,可以得出Rf电阻值与一批电阻中出现该电阻值概率的关系。
cdf为累积分布函数,为随机变量X取一个小于或等于某个x值的概率。即如果得到pdf,可以利用积分计算cdf。您可能采用高斯或正态分布的pdf,由两个参数定义:平均值(中心值)和标准方差(约等于峰值宽度)。图2给出了正态分布的pdf和cdf。

图2. PDF和CDF示例
正态分布与大多数实际情况相吻合,更容易建立数学模型。但是,请务必注意!正态分布可能并不真的代表某种特定情况。例如,如果您正在使用的是20%容差的电阻,可能容差为5%的电阻已全部被筛选出去,并被出售给其他人,您看到的实际pdf如图3所示。

图3. 筛选元件的分布情况
按照这种分布,测量电阻与电阻标签完全相同的概率为零!与使用正态分布的元件电路相比,您的电路所提供的性能会很差。另外,获得5%电阻的用户则会得到比较好的工作特性,因为他们所得到的元件的概率分布函数中已经消除了偏差较大的部分。
由此可见,可供选择的分布函数有许多,而如何选择分布非常重要。因此,不要局限于正态分布这一种。
在Excel中产生随机元件值
如果能够生成一系列随机数,即可用这些数值代表生产中所使用的电阻值。然后,用这些数值和电路公式确定电路的增益,将其与规格要求相对比,计算良率。下列各图是我完成的情况。就20次电路构建、±20%的增益误差而言,良率为80% (每次运行的结果会略有不同)。
图4. 生成随机电阻值
上述分析中,每个电阻均使用了均匀分布随机变量。这种均匀分布下,取值在两个极限值之间的概率都一样。可以使用两种方法生成电阻值:选择Tools | Data Analysis | Random Number Generation,或使用RAND()函数(请参考RANDBETWEEN() )。如果采用RAND()函数,电子表格每次计算便重新产生一个数值(按F9键)。
不幸的是,大多数元件所遵循的概率分布并非均匀分布。但是,这类分析在估计最差性能时较为快速和有效。
Excel提供了大量其它函数,可以帮助我们生成更为真实的pdf。我们将在下节对其进行介绍,之后叙述利用生产数据生成任意pdf的一些方法。
正态分布PDF和CDF
为了生成一种正态或高斯曲线,我们采用了内置函数NORMDIST()。例如,对于平均值 = 0,标准方差 = 1的正态分布,“=NORMDIST($A7,0,1,FALSE)”返回x = 存储于单元格A7的概率。标准方差(通常称为Σ)描述了pdf函数峰值的宽度,相当于二次求导的极性变化分界点,我们利用该方法生成图2所示pdf。通过将“FALSE”改变为“TRUE”,可以得到cdf值。
如果没有更准确的信息,则假设元件的百分比容差为±3标准方差。例如,±10%的元件会具有±10/3的标准偏差,标称值为±3.33%。
尽管cdf和pdf正确地描述了正态随机变量,但它们不生成随机元件值。理想状态下,我们会倾向于使用类似于“RANDNORM()”的函数,所返回的随机数符合正态分布。
生成正态分布随机数
Excel没有提供RANDNORM()函数,但是一些附加函数提供了这种必要功能。要想生成10个标称值为1kΩ,具有±20%误差范围的电阻值,步骤如下:- 平均数 = 1kΩ标称值,标准方差为1kΩ的±20%除以3 = ±200/3 = ±66.67Ω。
- 选择Tools | Data Analysis | Random Number Generation,使用内置函数生成一个数列。对话框如下图所示。

图5. 生成随机数的对话框
注意,我已输入步骤1中计算得到的平均数和标准方差。输入数字10,表示要生成的随机数(值)个数。输入电子表格中要求Excel输出值的位置。输出结果如下:

图6. Excel生成的随机元件值
其它有用的内置分布
您可能已经注意到,在Tools | Data Analysis | Random Number对话框中,Excel列举了多种分布供您选择。这些分布包括正态分布、均匀分布、二项式分布、伯努利分布、离散分布以及其它几种分布。前面所述的均匀分布是一种估计最差性能的简单、有效方法。二项式产生一种只有2个值(例如:1和0)的分布,常见于逻辑电路。一本好的统计学参考书和一些实验可以帮助选择正确的分布。如果特定分布于所提供的分布不一致,可以专门制作所需要的随机数生成器!我们将在下一节对此进行介绍。生成与生产数据一致的随机数
有些情况下,无法找到适合的内置函数或标准pdf函数。正如我们筛选电阻中所遇到的情况(图3),非标准分布的影响极其明显。这种情况下,我们会想要描绘一种分布,利用生产测试数据创建一种分布或者使用计算数据创建一种分布,然后生成符合这种分布的随机数,以进行良率分析。
创建此类分布以及符合这种分布的随机数,包括如下几个步骤(如后面图7所示)。
- 测量大量的实际元件或通过计算生成数据。也许能够在进货检验时获得这些数据。这种原始数据将被用于创建pdf。
- 将数据制作成直方图,并根据采样总数进行规一化,即所有概率的和为1。这种规一化的直方图便是我们需要的随机数的pdf。
- 对该pdf求积分创建cdf。确认能够单调达到最大值1。
- 生成一个介于0和1之间的均匀分布随机数—y~UY(0,1)。
- 将该均匀分布随机数用作cdf上y = P(X ≤ x)时cdf的指数,并记下x。
- 重复步骤4和5,生成所需要的x随机值。

图7. 生成与生产数据一致的随机数
 电子发烧友App
电子发烧友App


























评论