关键词:数字水印,四叉树,时域变换,压缩
1 引 言
数字水印的研究已经过几年的发展,它主要用于网络媒体知识产权的保护及认证。下面对目前比较成熟的方案作一简单介绍。
(1)利用DFT、DCT变换实现的水印技术。它们的共同点是将需嵌入水印的图(以下简称目标图)分割成8×8像素的不重叠方块,然后将这些目标图方块进行DFT或DCT变换形成8×8频域系数矩阵,再将水印嵌入到系数矩阵之中,最后,将系数矩阵反变换到空间域,再拼合成目标图,于是目标图中带有水印信息。不同之处在于对水印本身的处理、嵌入频段及深度,如:在嵌入水印时嵌入深度取决于被嵌入系数的反比值〔1〕,将水印分成两部分在两个中频范围内嵌入〔2〕,水印嵌入深度依赖于图像的局部特性〔3〕,将水印重复嵌入系数矩阵的指定位置〔4〕,将水印分别嵌入系数矩阵的中高频和低频部分〔5〕,将水印信号滤波后再嵌入系数矩阵〔6〕。8×8方块与JPEG压缩所采用的方块大小是一致的,因此,这类水印具有抗JPEG压缩的特性。这种水印技术的缺点在于完成空域与频域变换需要大量的运算时间,且频域的量化将对目标图产生较大的误差损失。另外,由于固定的8×8像素的分块模式,使嵌入水印后的目标图难免有按方块分布的噪声现象,对目标图的视觉质量有一定影响。
(2)不进行频域变换的水印技术最典型的是在LSB(最少意义位)上嵌入水印〔7〕,其目的是检测被嵌入图是否被非法修改,该算法对目标图视觉效果影响较小,而且,由于其对操作的敏感性,使图像所有者获得了感知非法攻击的敏感性。
(3)基于小波变换的水印技术一般是对目标图进行小波分解,然后将处理后的水印嵌入到小波系数之中,文献〔8〕对水印进行了伪随机处理,而文献〔9〕对水印实现了DCT变换,目的都是将水印变换为噪声形式以保证所有者的检知特权。基于小波变换的水印根据嵌入的深度和范围表现为鲁棒性或脆弱性,因此,目前对这种方式的评价还没有一个相对统一的结论。
我们提出一种基于四叉树的数字水印方法,先通过一种基于四叉树的灰度图像压缩方案,来使目标图实现无损到有损可调的压缩及空域变换,使目标图在嵌入水印后不呈现加噪现象,水印均匀分布于目标图的各个均匀区域。再对水印进行分层压缩并使之噪声化。最后,将水印嵌入到变换后的目标图之中。预计实验目标:嵌入水印后的目标图具有良好的视觉效果,以及较高的PSNR(峰值信噪比)值;被提取的水印具有可识别性,具有较高的NC(Normalized Correlation)值。提出的数字水印技术具有抗破坏能力:嵌入水印的目标图经过JPEG压缩、加噪、平滑、锐化、划痕、剪切等处理后,所提取的水印具有可识别性。
2 水印的嵌入和提取
首先,将目标图经时域变换分离成四叉树结构及去除冗余后的像素线性表〔10〕,再将压缩处理〔11〕后的水印嵌入到像素线性表中。实验证明,本方法处理后的已加入水印的目标图具有极好的视觉效果(不像经过DFT或DCT变换后的水印产生噪声现象),对加入水印的目标图经任何比例的JPEG压缩后,所提取的水印均具有可识别性。另外,本文的方法对于水印图像要 求宽松,利于用户随意构造不同大小、不同形状的水印来表达自己的信息。
2.1 目标图和水印图变换

其中,i指定树的中间结点,j指定树的叶结点,N2表示树中间节点之和,N3表示树叶节点之和。
pk为像素取值,像素在线性表中的位置k与S中的每一个叶结点j一一对应。
分离后的S和P可经TREE(·)的反函数及恢复函数ANT-TREE(·)恢复成目标图O:
假定二值水印图为
W={wn|0≤n≤M1×M2}
2.2 水印的嵌入
将W′经嵌入函数EMBED嵌入目标图O的像素线性表P中,形成P′:

2.3 水印提取
加入水印后的目标图O′经过网络上的流动和各种处理后,成为O″,要提取水印,先要进行结构和像素分离:
然后,经水印嵌入EMBED()的反函数即提取函数EXTRACT()提取水印:

3 实验结果及分析
3.1 图像选取与衡量标准
我们选取了具有代表性的Lena(256×256)灰度图作为目标图,选二值图Hust(64×64)作为水印图(图1)。
为了衡量图像质量,用PSNR(峰值信噪比)说明灰度图,用NC(Normalized Correlation)〔10〕说明二值图,计算公式如下:

3.2 视觉效果分析
水印嵌入后的Lena′(图2)有很好的视觉效果,其PSNR也是理想的。
从图2可知,嵌入水印后的Lena′在视觉上与原图没有任何差别,同时也不存在任何噪声现象。这是因为我们在嵌入水印时,将水印嵌入到目标图四叉树的像素线性表中,而线性表的每一个像素实际对应图中的一个灰度均匀的方块,每一个水印位分布于均匀块的每一个位置上,因此,不可能有颗粒状态,均匀块灰度的微小变化是肉眼不能觉察的。
3.3 抗压缩能力
图3显示了Lena′经JPEG压缩后其压缩品质(使用Photoshop6.0进行压缩),与所提取的水印Hust″的NC构成的关系曲线(在计算NC时认定经过水平平移后的水印与原水印无本质差别)。
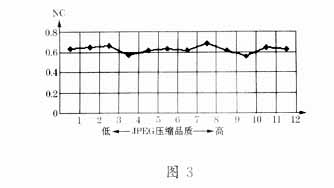
由图3可知,经JPEG任意比例压缩后的目标图中所提取之水印是可识别的,说明我们提出的水印方法是抗JPEG压缩的。值得注意的是,JPEG压缩的压缩比并未对NC值造成明显的影响,NC始终接近或高于0.6,这是本方案显著优于其它水印方案的地方,如采用DCT变换目标图后嵌入水印的方案,在增大JPEG压缩力度时,所提取水印的NC明显下降直到接近0〔9〕〔5〕。
3.4 抗其它处理的能力

图4为各种处理后的水印效果图,由此可见,本水印方法的抗处理能力。图4中:(a)目标经过90度旋转,(b)目标被压缩至0.15bpp,(c)目标中加入1%的白噪声。
图5中的目标图经过了较大的破坏和剪切,从中提取的水印依然可识别。

其它方案一些图像破坏处理的实验结果见图6,由此可看出本水印方案的抗图像翻转能力、抗高斯噪音能力和抗高频滤波能力。这些能力是突破水印技术难题的关键。图6中:(a)经过180度翻转,(b)加入高斯噪音,(c)经过锐化处理。
4 结束语
本文提出的一种基于时域变换的数字水印算法,将目标图时域变换为四叉树结构和有效像素线性表,将水印嵌入像素线性表中。由此产生的已嵌入水印的目标图无噪声现象,有良好的视觉质量和理想的PSNR,说明该方法的水印隐藏效果好。加入水印的目标图经过各种处理(特别是JPEG压缩、划痕和剪切)后所提取的水印依然是可识别的,证明该方法具有较好的鲁棒性。在水印嵌入和提取时设置了水印大小、嵌入位置、嵌入次数和嵌入深度四个变量,使水印的选取和加入具有很大的灵活性。加上时域处理明显在时间和空间复杂性上低于频域处理,使本方法在高精度图像的处理上占有优势。
实验证明,我们的方法在提高已嵌入水印图的视觉质量、降低算法复杂度、保证水印的鲁棒性、提高水印的隐藏性方面均达到预期目标,其中大部分指标超过已有的水印方案所公布的指标,是一种综合特性好的水印技术。
下一步的工作是研究提高水印NC值的方法,进一步提高提取的水印精度。
2 S Pereira,JJK O Ruanaidh,F Deguillaume,et al..Template Based Recovery of Fourier-Based WatermarksUsing Log-Polar and Log-Log Maps.IEEE InternationalConference on Multimedia Computing and Systems,1999,Vol1:870~874
3 Y Choi,IAizawa.DigitalW atermarking Using Inter-BlockCorrelation.Proceedings ofthe InternationalConference onImage Processing(ICIP99),1999,Vol2:216~220
4 夏光升,陈明奇,杨义先,等.基于模运算的数字水印算法.计算机学报,2000(11):1146~1150
5 周四清,余英林.互补性图像水印算法的研究.计算机工程与应用,2000(11):29~31
6 孟 兵,周良柱,万建伟.基于维纳滤波的数字水印算法.计算机工程与应用,2000(11):96~98
7 M M Yeung,F Mintzer.An Invisible W atermarkingTechnique for Image Verification.Proceedings of theInternational Conference on Image Processing,1997,vol2:680~683
8 A Lumini,DMaio.A Wavelet-Based Image W atermarkingScheme.Proceedings of the International Conference onInformation Technology:Coding and Computing,2000: 122~127
9 JS Cho,SW Shin,W H Lee,et al..Enhancement ofRobustness ofImage Watermarks Embedding into ColoredImage Based on W T and DCT.Proceedings of theInternational Conference on Information Technology:Coding and Computing,2000:483~488
10 颜 彬,陈传波.基于时域变换的失真度可调图像压缩算法.计算机应用,2002(11):14~17
11 颜 彬,陈传波.基于四叉树的二值图像时域分层压缩算法.计算机工程与应用,2002(9):69~71
 电子发烧友App
电子发烧友App





















评论