简介
本文从电气工程师的观点 (POV) 出发,重点研究了给定处理器的实施和如何在各种实施方式下进行权衡。软件工程师关于程序执行中的多线程、并行处理或者再配置的观点不在本文的考虑范围之列。程序执行的主要方面包括速度、精度、面市时间 (TM) 和存储器利用等。另外,编码标准、IP 维护、便携性和文档等其他因素仅影响将来项目的 TM,对目前的程序没有影响。因此,在本文的案例研究中只考虑主要的方面。在理想的情况下,我们希望能够把程序执行的每个方面都是最优秀的,但实际的系统并非完美,需要有所取舍。本文将探讨在程序实施中权衡使用公式法和 LUT 的情况,并探讨各方面下表现最佳的方法。实施方法的选择将取决于应用的具体要求。
LUT 是存储在系统存储器中的预期结果范围列表或者阵列。使用测得的输入值作为索引,就可以在执行中得到输出值,从而节约处理时间。LUT 可以通过多种方式建立。大多数工程师除了需要具备工程领域内的各项技术技能,也同时还需要具备“Excel 工程设计”技能,因此,本文将采用 Microsoft Excel 表格创建 LUT。将预期的输入范围输入公式,即可在 LUT在得到对应的输出值。与执行传统的数学公式相比,使用 LUT 系统具有多种优势。
执行速度
Accuracy
在完整的系统中,输入和预期输出之间的延迟来自硬件、软件、中断和逻辑驱动延迟。数据处理和分析也会影响程序中的软件延迟。数据处理取决于实施指令所需要的时钟周期数量。简单来说,与 LUT 方法访问存储器中的值相比,公式法使用的乘、除或者其他复杂的数学函数耗用的 CPU 周期更多。尽管可以采用移位法和加减法算法来完成乘除运算,提高公式法的速度,但在大多数情况下对简化等式及提升效率和精度的作用微乎其微。因此,LUT 法一般都会快于公式法。
精度
在精度方面,公式法一直优于 LUT 法。由于我们采用的是电气工程师的视角,我们不妨在执行方法和电气信号之间进行一下类比。公式法类似于连续时间模拟信号,而 LUT 则类似于量化的离散信号。无限样本的 LUT 可以达到公式法的精度。LUT 的精度取决于考虑的范围和范围中的样本数量。因此,根据要求的精度和范围,LUT 的存储器利用是可扩展的。
存储器利用
公式法中的存储器使用主要取决于用于等式执行的代码空间大小和支持这些等式的数学库的大小。如果采用单浮点函数则需要添加整个库,存储器耗用会显著增长。在 LUT 法下,存储器耗用取决于用来解析 LUT 获得输出值的代码大小和LUT 的大小。一般而言,实施公式和解析 LUT 的代码空间差别不大,但库对存储器的占用显著高于 LUT 的大小。LUT 的大小是由要求的精度决定的,并可通过插值法进行优化。因此,在应用要求的公式比较复杂,输入范围又较小的情况下,LUT 对存储器的利用效率更高。
面市时间
由于早已开发完毕,并在大多数系统上得到过验证,因而在直接采用公式的情况下,面市时间会更快。这样既能达到要求的精度,又能节省设计、调试和测试系统的时间。在某些项目中,存储器可能不足以满足公式法使用的数学库的要求。在这种情况下,则需要采用分段线性或 LUT 法。LUT 法的 TM 取决于多种因素,如应用复杂性、工程师技能、可用于构建 LUT 的软件工具等。因此,这项参数无法以量化的方式进行比较。不过,由于与具体的系统/平台无关,公式法的实施速度可能会快一些。
本文就应在什么地方使用 LUT 取代公式的两个示例及其涉及的权衡进行了探讨。所探讨的案例中包含程序执行的不同重点方面。第一个例子是含有复杂的数学等式的温度感应应用。因为采用公式法来获得温度值耗用了大量的存储器,留给根据测得的温度值增添其他功能的存储空间则变得更少了。通常,温度感应是完整的感应器系统的一部分,因此存储器优化在该应用中非常重要。第二个例子是控制系统算法。在该例中,为避免系统不稳定情况的出现,执行速度是最需要考虑的。
案例研究1:温度测量
因其阻值随温度而发生变化,热敏电阻通常被用来测量温度。采用负温度系数(NTC) 的热敏电阻测得的温度 (Tk) 与测得的阻抗 (RT) 呈反比关系,可表达为等式1 中的 Steinhart-Hart 公式。
[1]
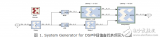
等式中的 A、B、C 均为常数。为测得阻抗变化,可考虑图 1 所示的系统。在此图中,VT 为热敏电阻两端的电压,Vref 为恒定参考电压。ADC 的输出是 VT 点模拟电压的数字形式。固件根据 ADC 测得的值,采用各种实施方案计算出相应的温度值。
.

图 1:采用热敏电阻的温度感应系统方框图
图中文字:thermistor:热敏电阻
firmware data processing:固件数据处理
temperature value 温度值
公式法:
在公式法中,热敏电阻的阻值使用标准的分压方程式计算,如等式 2 所示。
[2]
这里的 VGND 和 Vref 可在程序中定义为常数,也可测量得出。将测量得出的值代入等式 2,可以消除因参考电压变化、ADC 增益和偏置变化引起的误差。在本文中,假定参考电压、ADC 是理想的,且Vref 和 VGND均为常数。在计算出阻值后,就可以使用等式 1 计算出温度值。
因为等式 1 不是简单线性等式,在采用公式法的情况下,有效的存储器利用和执行的速度都很重要。这个等式必须加入较大的数学库。是否因为精度而接受较大的存储器占用和较慢的反应速度,取决于应用的需要。在医疗或太空设备中,精度非常重要,而在家用电器中,精度并不是最重要的因素,比如我们在安保系统、炉具或者轿车中所见到的温度测量。在这些应用中,如果外部温度是 70 度,而感应系统显示 71 度,并不会导致致命的结果。消费者也不愿意化更多的钱购买功能更强大的芯片来获得这种精度。
针对热敏电阻的 LUT
热敏电阻的电压会一直对应一个唯一的阻值,也就是唯一的温度值。例如,如果 NTC 热敏电阻在 25 摄氏度的阻值为 RT=10 KΩ,参考电阻为 Rref=10 KΩ 时,则意味着 25 摄氏度时的电压 VT=Vref/2。在温度为 50 摄氏度时,RT=5 KΩ,不过 Rref 和 Vref 保持不变,故VT=Vref/3。因此,VT=Vref/3 就意味着 T=50 °C,而VT=Vref/2 意味着 T=25 °C。这样就可以根据测得电压对应的温度值使用等式编制一张表格,存储在存储器中作为 LUT。然后使用测得的电压值作为索引来解析LUT,进而获得对应的温度值。决定温度步长的LUT 的大小会影响测量的精度。如果要求的温度范围为 –40 ~ 125 °C,则在步长为 1 °C 的情况下需要有 166 条目的 LUT,如果是 0.5 °C,就需要 332 条目的 LUT。因此在精度、测量范围和存储器使用方面存在大量的权衡空间。在公式法下,不管要求的精度和测量范围如何,存储器使用都是固定的。
比较
包含 LUT 法和公式法的项目都在赛普拉斯软件 PSoC Designer 中借助 CY8C27x43 芯片得到了实施。LUT 的大小如前所述,为 166 条样本。LUT 法使用的 ROM 为1,000 字节,而在公式法中为 3,780 字节。如果项目在带有 4K 存储器的芯片上实施,则剩下的闪存对任何复杂系统均不敷使用。
为比较执行速度,分别运行了两种方法。如图 2 所示,每种方法运行完毕后,都会触发一个引脚。

图 2:热敏电阻感应系统的执行时间
对应执行公式法耗用时间的信号电平较低,对应执行 LUT 法耗用时间的信号电平较高。如图所示,LUT 法耗用的时间为 8µs,公式法耗用的时间为 468 µs。虽然速度方面的比较取决于处理器时钟速率和用于实施的 CPU 时钟周期,但本案例大致说明了两者之间的差异。显而易见,在本应用中,LUT 法可以将执行时间降低 50 倍。
案例研究2:PID 系统
比例-积分-微分 (PID) 系统是最常见的反馈控制系统(如稳压器等)。采用专门的硬件,可以获得最快的控制环路响应时间。不过,如果采用微处理器来实施 PID 系统,可以支持更多调试和调整 (adaptation) 功能。本案例研究的两种实施方法均采用 SoC。图 3 所示的是 PID 系统的实施方框图。

图 3:PID 系统方框图
图中文字:plant:设备
error:误差
firmware data processing:固件数据处理
output:输出
PID 稳压器系统具有需要的置位点 Vset 和实际输出电压 Vout。需要的信号和输出信号之间的差就是误差值e。控制环路然后运用等式 3 所示的闭合环路系统等式来让误差值为 0:[3]这里的 Kp、Ki和Kd 均为常数。
公式法
在 PID 系统的软件实施方案中,积分/差分是通过对上一误差值和新的误差值进行累加/累减来实现的。这些值然后与等式 4 所示的相应常数相乘。
[4]
这里的 ErrorI 是添加到现有误差值中的上一累加误差值,ErrorD 是从现有误差值中减去的上一累减误差值。得出的新值存储为上一误差值并用于下一个执行周期。由于等式中有乘法运算,因此执行速度较慢。
LUT 法
在 LUT 法中,程序不使用乘法,其使用的是存储在表中的预先生成的误差值与常数相乘的积。测得的误差值被用作在对应的表中获得输出的索引。因此,误差值仅限于整数值而非浮点数,因此也就限制了精度。采用这种方法的指令如等式 5 所示:
[5]
这里 TableP、TableI和 TableD分别为包含 KP*Error、Ki*ErrorI和 Kd*ErrorD值的 LUT。
比较
PID 系统的实施是采用赛普拉斯软件 PSoC Designer 在 CY8C27x43 芯片中进行的。为实施 LUT 法,使用了各存有 60 个值的三张表,使用的 ROM 为 1,150 字节。对同一应用,公式法需使用 1,800 字节的 RAM。两种方法的执行时间如图 4 所示。

图 4:PID 系统的执行时间
上图波形与图 2 相似,高电平信号对应的是 LUT 法的执行速度,低电平信号对应的是公式法的执行速度。显而易见,执行速度提升了 4 倍。
结论:
本次探讨及案例研究显示,LUT 法确实能够加快程序执行的速度。对于具体的应用,程序执行中还有其他需要在选择实施方法之前加以权衡的问题。最终选择哪种方法则取决于应用的规范。不过,如果旨在加快执行速度并减少存储器占用,则化费时间构建 LUT 也是在所不惜的。
 电子发烧友App
电子发烧友App






















评论