1 引 言
AES加密算法的一种优化的FPGA实现方法
随着密码分析水平,芯片处理能力和计算技术的不断进步,des的安全强度已经难以适应新的安全需要,其实现速度、代码大小和跨平台性均难以继续满足应用需求。因此,nist(美国国家标准与技术研究所)筹划aes(高级数据加密标准)算法,旨在取代des,以保护21世纪敏感政府信息的新型加密标准。rijndael算法以其简洁、高效、安全和原则性的设计被接纳为aes,并于2001年11月26日正式公布在fips(federal information processingstandards)出版的fips-pub 197中。作为des的继承者,aes自从被接纳为标准之日起就已经被工业界、银行业和行政部门作为事实上的密码标准。
随着网络传输速度提升为gigabits数量级,业界对算法的执行速度的要求也越来越高,基于软件的密码算法便显得性能不足,需要采用硬件加密的方式,他采用一些特殊的优化技术(如流水线和查找表等),可极大地提高数据的流量并减少密钥的生成时间。另外,用硬件实现加密算法及与之相关的密钥生成过程,并且封装到芯片中,因为他们不易被外部攻击者读取或更改,会有较高的物理安全性。因此,基于硬件的密码算法就受到业界的普遍关注。以fpga为代表的可重构硬件以其自身所固有的特点既具有硬件的安全性和高速性又有软件的灵活性和易维护性,已经成为分组密码算法硬件实现的热点研究方向。
本文介绍aes加密算法的一种fpga实现的方法以及对其加密速度的优化处理技巧。
2 aes加密算法简介
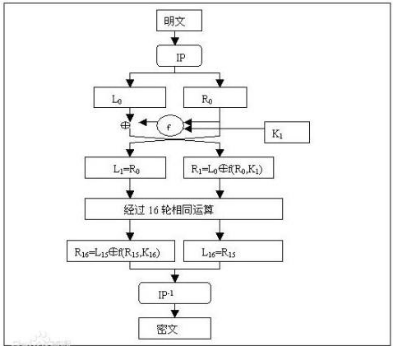
aes是一种迭代分组密码,采用的是代替/置换网络(spn)。他将明文分组长度固定为128 b,而且仅支持128,196或256 b的密钥长度,本文仅对密钥长度为128 b的情况进行讨论。
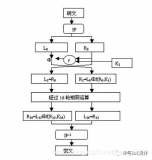
aes加密算法的实现包括密钥扩展过程和加密过程。加密过程又包括一个作为初始轮的初始密钥加法(addroundkey),接着进行9次轮变换(round),最后再使用一个轮变换(finalround),如图1所示。
每一次round均由subbytes,shiftrows,mixcolumns和addroundkey共4个步骤构成,finalround包含除mixcolumns这一步外的其他3个步骤,round结构如图2所示。
轮变换及其每一步均作用在中间结果上,将该中间结果称为状态,可以形象地表示为一个4*4 治疗大三阳去哪家治好b的矩阵。
3 aes加密算法的优化
3.1 字节代换(subbytes)
步骤subbytes是rijndael密码中惟一的非线形变换。他是一个砖匠置换,该置换包含一个作用在状态字节上的s-盒,用srd表示,他是由字节在gf(28)域中求其乘法逆并外加一个仿射变换(仿射变换的作用是复杂化s-盒的代数表达式)实现,假设该步的输入为a,输出为b,即b=srd(a)。由于该步骤是一种非线形面向字节的变换,是将一个8位二进制数据转换为另一个不同的8位二进制数据,这里要求一一对应,并且替换结果不能超出8位,可以通过构造可逆的s-盒来实现。
根据字节代换的要求和特点,具体实现时,可以将s-盒用一个16*16 b的置换表来表示,通过查表即可实现该步变换,避免了复杂的乘法运算。
3.2 行移变换(shiftrows)
shiftrows是线形变换,他和列混合运算相互影响,在多轮变换后,使密码信息达到充分的混乱,提高非线形度。
行变换是在状态的每个行间进行的,是状态中的行按照不同的偏移量进行循环左移运算,在明文分组长度为128 b,密钥长度为128 b时,shiftrows对状态的每行作用如下列表达式所示:
显而易见,可以通过对每个字节的移位简单实现该步变换。
3.3 列混合变换(mixcolumns)
mixcolumns是线形变换,是以状态的列为单位进行的操作。假设该步的一列的输入为a,输出为b,mixcolumns对状态的每列作用如下列表达式:
上述矩阵乘法为gf(28)有限域中的乘法运算,并且有一个因子为常数。由于gf(28)有限域中的每一个元素都能够写成02的不同幂次的和(例如:15=01○+022 ○+024),因此,乘以任何常数的乘法都可以通过反复的乘以02和异或运算来实现。可将矩阵乘法中的常数因子分解为02的不同幂次和,矩阵乘法转换为与02的乘法和异或运算。将gf(28)域中的每一个元素与02的乘积存储在一张16*16 b查找表中,记作xtime(?)(例如:02*a=xtime(a))。所以,该步骤可以通过查表和异或运算实现,表达式如下(假设该步的一列的输入为a,输出为b):
3.4 密钥加法(addroundkey)
addroundkey是将轮密钥中的各个字节与状态中的各个字节逐位异或,实现密码和密钥的混合。轮密钥是由初始密钥通过密钥扩展得到的。
3.5 密钥扩展(expandedkey)
以明文分组长度为128 b,密钥长度为128 b为例,expandedkey将初始密码密钥(初始密钥可以形象的排列成一个4*4 b的矩阵)作为初始密钥加法的密钥,以后的各轮轮密钥是经过下列表达式的密钥扩展函数得到的(k[i][j]表示初始密钥状态的第i行第j列,w[i][j]表示扩展后密钥状态的第i行第j列,nk表示密钥分组的列数,nr表示轮数,nb表示明文分组的列数,这里nk=4,nr=10,nb=4):
当nk6时:
其中,srd(?)是s-盒的置换表,rc(j/nk)是一个轮常量,用于消除对称,可以通过查轮常量的表来得到。
密钥的选取:第i轮的轮密钥就是由矩阵w中第nb*i列到nb*(i+1)-1列给出。
3.6 流水线结构
流水线结构是实现流程中加入寄存器和相应的逻辑电路,将整个过程划分为前后相连的多级实体,每一级只完成数据处理的一个步骤,一个时钟周期完成一级数据处理,然后在下一个时钟到来时将处理后的数据传递给下一级;第一组数据进入流水线后,经过一个时钟周期传递到第二级,同时第二组数据进入笫一级,数据队列依次前进。使一个时钟内有多个数据块同时在各级中处理。虽然每组数据都要经过整个流水线后才能得到最后的计算结果,但是作为整个流水线,每个时钟周期都能计算出一组结果,所以平均计算一组数据几乎只需要一个时钟周期的时间,大大提高了数据处理速度,保证了整个系统以较高的频率工作。
流水线技术通过同时处理多个数据块的方法提高吞吐量,其代价是硬件资源的增加。流水线结构只能用于非反馈加密模式。
4 实现及仿真
粗线代表数据线,细线代表控制线。控制信号从输入接口进入,数据和密钥通过数据总线进入,根据控制模块来进行数据传输,更换密钥和加密运算。
从第3节的分析可以看出,aes算法可以通过对srd表,xtime表和rc表的查询和通过组合逻辑实现的移位和异或运算来实现。这些实现方法代替了繁琐的乘法运算,提高了加密速度。
采用了流水线结构来同时处理多个数据块,提高吞吐量。
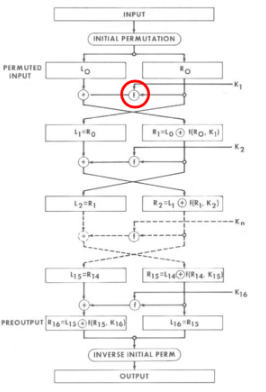
使用轮函数完全展开的开环结构,将轮函数划分成4级流水线,轮函数中的每一个步骤都是一级,并在级与级之间加入寄存器暂存中间状态的数据以消除竞争,从而实现了轮函教内部的完全流水,如图4所示。
其中,控制信号sel1,sel2.sel3干sel4分别是每一级(每一步数据)处理是否完成的标志。
在轮函数的外部,将每一轮函数都作为外部流水中的一级,从而实现了算法内部外部的完全流水结构,如图5所示。
其中,控制信号sel0~sel10分别是每一轮数据处理是否完成的标志。
由于采用流水线结构只能用于非反馈加密模式,所以aes算法的实现使用的是电码本模式(ecb)的工作方式。
密钥扩展这一步放在所有加密步骤之前进行。再先输入初始密钥,然后通过对srd表和rc表的查询和通过组合逻辑实现的移位和异或运算完成密钥的扩展,并将结果存储在一个176 b的寄存器中。在密钥扩展完成后再进行以后的数据加密,在进行每一轮的密钥法时,将直接在该寄存器中选择轮密钥。
针对afs算法和fpga的特点,对每一步的处理都采用以字节为单位的对寄存器进行操作的方式。往quartusii5.0中,用vhdl硬件描述语言实现了该算法,经过仿真,结果如下:
5 扩展及应用
迎过fpga来实现aes的解密算法(在此仅讨论分组长度为128 b,密钥长度为128 b时的情况),同样可以用查找表和简单的组合逻辑来实现。考虑到使用等价解密算法没有多少好处,所以选用直接解密算法,依旧可以采用轮函数内部外部完全流水的流水线技术来提高解密速度。
注意:
(1)解密算法中的逆字节代换这一步骤可通过查逆srd表实现。
(2)解密算法中的逆行移变换这一步骤可直接将状态的每一行循环右移实现,如下列表达式所示:
也可以将状态的第二行和第四行互换后进行加密算法中的行移变换,然后再将变换后的状态的第二行和第四行互换来实现解密算法中的逆行移变换这一步骤。这样就利用了加密算法中的行移变换的模块(此方法仅适用于分组长度为128 b的情况)。
(3)解密算法中的逆列混合变换这一步骤中,由玻尿酸隆鼻均价于矩阵乘法的系数为09,0e,0b,0d,如下列表达式所示(假设该步的一列的输入为a,输出为b):
可以通过一个预处理步骤和一个列混合变换步骤来实现,顸处理步骤如下列表达式所示(a是一列):
这样就利用了加密算法中的列混合变换的模块。
在同时支持加解密的模块中,密钥扩展和密钥加法的部分可以同时用于这两种模式,密钥扩展部分只须输入对应的肌密的初始密钥后做和加密同样的密钥扩展,然后按照解密所需要使用的轮密钥的顺序重新排列,存入寄存器等待使用即可,这样可以节约资源。
由此,可以将aes的加解密算法统一起来,在一个FPGA模块中实现。通过avr或arm等处理器的控制来选择fpga是执行加密过程还是解密过程以及是否更换新的初始密钥,形成完整的加解密模块,可作为单独的密码机使用或通过各种接口与计算机,工控机等其他主控设备连接完成对数据的加解密。
aes加解密算法可以应用于虚拟专用网、sonet、远程访问服务器、高速atm、以太路由器、移动通信、卫星通信、电子金融业务等领域,为其提供安全、可靠、快速的解决方案。
STM32/STM8
意法半导体/ST/STM
 电子发烧友App
电子发烧友App


























评论