频分复用(OFDM)系统的原理

On wireless communication,the high rate and high quality of communication service are required to offer,and OFDM has the advantage of the high bandwidth efficiency and strong anti-multipath ability ,so OFDM receives widespread attention in recent years. OFDM is actually one kind of multi-carrier modulation .and the main idea of OFDM is Channel will be divided into several subchannels orthogonal,and then turn High-speed data signals into parallel low-speed data-flow , modulation in each of the subchannels on transmission.
The design is the use of MATLAB design a structured, modular, graphical simulation software. To provide simulation platform for OFDM technology. OFDM is required to complete the simulation modeling. The major signal mapping, modulation, and other sub-module . Signal mapping module which is based on the corresponding modulation encoding each bit Table Group into a plural . After string and the conversion of binary data , Road map on each divided into two groups a bit, By map the QAM constellation into plural. By using look-up table method QAM constellation is mapped. QAM constellation is drawn. And modulation or demodulation module can be used to achieve IFFT or FFT . OFDM systems are used more coherent demodulation. When receiver data is demodulation, Channel estimation need to correct by the frequency selective fading and sub-carrier frequency offset the random phase shift and the magnitude of the decline. Otherwise, the bit error rate performance is very difficult to achieve practical requirements. Channel estimation is used LMS channel estimation algorithm. Finally additive white Gaussian noise channels of signal-to-noise ratio (SNR) - bit error curves is drawn.
KEY WORDS wireless communication, multicarrier modulation, OFDM, Channel Estimation

目 录
摘要 I
ABSTRACT II
第一章 绪论 1
1.1正交频分复用（OFDM）的来源 1
1.2 正交频分复用（OFDM）的研究背景 1
1.2.1 无线通信的发展 1
1.2.2 第4代（4G）无线通信系统 2
1.3正交频分复用（OFDM）的意义 2
1.3.1正交频分复用（OFDM）的优点 2
1.3.2 正交频分复用（OFDM）的不足之处 4
1.4 多载波技术的发展 4
第二章 频分复用（OFDM）系统的原理 6
2.1 多载波调制基础 6
2.2 频分复用（OFDM）系统的技术原理 6
2.2.1 OFDM的基本原理 7
2.2.2 信号映射(mapping) 7
2.2.3 OFDM系统的数学模型 11
2.2.4 用DFT实现OFDM的调制与解调 14
2.2.5 FFT/IFFT 14
2.2.6保护间隔和循环前缀 15
2.2.7 交织 17
2.2.8 OFDM的同步技术 17
2.2.9 OFDM系统的重要参数设计 18
第三章 OFDM系统的仿真设计 20
3.1 OFDM的MATLAB仿真 20
3.1.1 MATLAB语言简介 20
3.1.2 正交频分复用（OFDM）仿真系统说明 21
3.1.3 仿真程序说明 23
3.1.4 调试过程和结果分析 33
第四章 结束语 35
4.1总结 35
4.2不足与展望 35
致谢 37
参考文献 38

摘要
在无线移动通信中，要求提供高速率和高质量的通信服务，而正交频分复用(OFDM)因具有频带利用率高和抗多径能力强等优点，近年受到广泛的重视。OFDM(正交频分复用)技术实际上是多载波调制的一种。其主要思想是：将信道分成若干正交子信道,将高速数据信号转换成并行的低速子数据流,调制到在每个子信道上进行传输。
本设计是利用MATLAB设计一种结构化，模块化，图形化的仿真软件，为OFDM技术的研究提供仿真平台。要求完成OFDM的仿真建模，主要完成信号映射，调制等子模块的演示。其中信号映射模块主要是根据相应的调制编码表把每个比特组转换成一个复数。经过串/并转换的二进制数据，每一路按映射方式分为2比特一组，按QAM的星座图映射成复数。而调制/解调子模块可以用IFFT/FFT来实现。OFDM 系统中更多的采用相干解调，接收端解调数据时，需要信道估计来纠正由频率选择性衰落和子载波频率偏移产生的随机的相位偏移和幅度衰落，否则系统的误码率性能很难达到实用要求。本文中信道估计采用了LMS信道估计算法。最后得到在加性高斯白噪声信道下的信噪比（SNR）－误码率曲线图。
关键词：无线移动通信，多载波调制，正交频分复用，信道估计
ABSTRACT
第一章 绪论
1.1正交频分复用（OFDM）的来源
进入21世纪以来，无线通信技术正在以前所未有的速度向前发展。随着用户对各种实时多媒体业务需求的增加和互联网技术的迅猛发展，可以预计，未来的无线通信技术将会具有更高的信息传输速率，为用户提供更大的便利，其网络结构也将发生更本的变化。目前普遍的观点是，下一代的无线通信网络将是基于统一的IPv6包交换方式，向用户提供的峰值速率超过100Mbit/s【1】,并能支持用户在各种无线通信网络中无缝漫游的全新网络。为了支持更高的信息传输速率和更高的用户移动速度，在下一代的无线通信中必须采用频谱效率更高，抗多径干扰能力更强的新型传输技术。在当前能提供高速率传输的各种无线解决方案中，以正交频分复用（OFDM）为代表的多载波调制技术是最有前途的方案之一。
1.2 正交频分复用（OFDM）的研究背景
1.2.1 无线通信的发展
人类采用无线方式进行通信的历史可以追溯到19世纪末。1864年，英国物理学家麦克斯韦（J.C.Maxwell）创造性地总结了人们已有的电磁学知识，预言了电磁波的存在。1887年，德国物理学家赫兹（H.R.Herts）用试验产生出电磁波，证明了麦克斯韦的预言。1897年，意大利科学家马可尼（G.Maroni）和俄国军官波波夫（A.S.Popov）首次使用无线电波进行信息传输并获得成功。1901年，马可尼实现了从英国到纽芬兰的跨大西洋无线电信号接收，这是一次超过2700公里的远距离通信，充分显示了无线通信的巨大发展潜力。在随后一个多世纪的时间里，伴随者计算机技术和大规模集成电路技术的发展，无线通信的理论和技术不断取得进步，今天的移动通信技术已成为人们日常生活中不可缺少的重要通信方式。
早期的无线通信主要用于船舶，航空，列车，公共安全等专用领域，用户数量很少。20世纪60年代，贝尔实验室提出了蜂窝的概念，使无线通信摆脱了传统的大区制结构，为无线通信的大规模商用奠定了基础。20世纪70年代，具有高可靠性的固态微型射频硬件的发展使移动通信逐渐成熟起来。从20世纪70年代末到现在的20多年时间里，无线通信系统从第1代发展到了第3代，进入一个飞速发展的时期。据统计，1990年全球蜂窝电话的用户仅为1千万，而目前蜂窝电话的用户的数量已达到7亿。在中国，目前蜂窝电话的用户已超过1.4亿，每月新增蜂窝电话的数量将超过1500万，移动通信市场出现了空前的繁荣。见文献[1]。
1.2.2 第4代（4G）无线通信系统
根据无线通信每10年发展一代的特点，20世纪90年代末自ITU-R推出3G移动通信的标准之后，各个国家和地区为了在下一代无线通信系统的标准中占有一席之地，纷纷启动了新一代无线通信系统的技术和标准化研究工作。有关新一代无线通信系统的名称目前尚不统一，这些名称有4G，Beyond3G,Beyond IMT-2000等多种，在此，我们将其统称为4G无线通信系统。
对4G系统研究最为积极的地区和国家当属欧盟，美国，东亚的日本，韩国和中国。欧盟的研究工作主要包括欧盟信息技术协会（IST）第5框架和第6框架研究计划下的多个研究项目（如MIND,Moby Dick,OverDRIVE,SCOUT,MATRICE等）以及世界无线通信技术研究坛（WWRF）的工作。美国对4G的研究比较分散，主要体现在美国电器与电子工程师协会（IEEE）主办的各种会议和研讨会上发表的有关4G系统的报道，DARPA资助的下一代（XG）通信系统的研究计划和MIT正在进行的Oxygen研究项目。日本的4G系统研究机构主要有移动信息技术论坛，日本通信技术研究所（CRL）和NTTDoCoMo公司。目前，NTTDoCoMo公司的4G研究工作非常引人瞩目，他们提出了基于正交频率码分复用（OFCDM）技术具有可变扩频因子的4G系统实现方案，并于2002年10月推出了下行链路速率为100Mbit/s【1】，上行链路速率为20Mbit/s的试验系统。在韩国，对4G移动通信系统的研究工作主要由韩国电子通信研究所（ETRI）来承担，目前，ETRI已经确定了4G系统的远景目标和研究时间表，并与国内外的大学和研究机构密切协作，全力推动4G系统的标准化工作。在中国，2001年启动的”十五”863重大研究计划项目中专门设立了面向4G的FuTURE计划，该计划的研究目标是在新技术产生的初期，对国际主流核心技术的发展以及知识产权的形成有所贡献，实现移动通信技术跨越式发展，开展高技术研究和试验，侧重于可实现性的关键技术开发与演示，并于2005年底进行关键技术的演示。
1.3正交频分复用（OFDM）的意义
1.3.1正交频分复用（OFDM）的优点
宽带无线通信系统中存在的主要问题是频率选择性衰落所引起的符号间干扰（ISI）问题。传统上克服ISI的方法有两种：第一种方法是采用单载波调制加时域均衡的方法，如2G蜂窝系统GSM中即采用了这种方法；第二种方法是采用直接序列扩频码分多址（DS-CDMA）加Rake接收技术，如2G蜂窝系统IS-95和3G蜂窝系统IMT-2000中均采用了这种方法。上述两种方法在各自的系统中都能很好地克服因频率选择性衰落所引起的符号间干扰问题，但是，对于高速数据业务来说，传统的单载波系统和CDMA系统都存在很大的缺陷。由于无线信道存在时延扩展，而且高速信息流的符号宽度又相对较短，所以符号之间会存在着较严重的ISI，由此对单载波系统中所使用的均衡器提出非常高的要求，即抽头数量要足够大，训练符号要足够多，训练时间要足够长，这样均衡算法的复杂度也会大大增加。对于CDMA系统来说，其主要问题在于扩频增益与高速数据流之间的矛盾。在保证相同带宽的前提下，对高速数据流所使用的扩频增益不能太高，否则就大大限制了CDMA系统噪声平均的优点，从而使系统的软容量受到一定的影响，如果保持原来的扩频增益，则必须要相应地提高带宽。此外，受系统实现复杂度的限制，CDMA系统中Rake接收机的分支数量不能太多（目前为5左右），在高速宽带系统中可分解的多径数量较多，此时会有较大的能量损失。
近年来，备受人们关注的一项宽带传输新技术是以正交频分复用（OFDM）为代表的多载波传输技术【2】。多载波传输技术【3】把数据流分解为多个独立的子比特流，这样每个子数据流将具有低得多的比特速率，用这样的的低比特率形成的低速率多状态符号再去调制相应的子载波，从而构成多个低速率符号并行发送的传输系统。正交频分复用（OFDM）是多载波传输方案【4】的实现方式之一，在非对称数字用户线（ADSL）中，正交频分复用（OFDM）也被称为离散多音（DMT）调制。正交频分复用（OFDM）利用逆快速傅利叶变换（IFFT）和快速傅利叶变换（FFT）来分别实现调制和解调，是实现复杂度最低，应用最广的一种多载波传输方案。除了正交频分复用（OFDM）方式之外，人们还提出了许多其它的实现多载波调制的方式，如矢量变换方式【5】，基于小波变换的DWMT方式【6】，采用滤波器组的滤波多音（FMT）调制方式【7】等，但这些方式与正交频分复用（OFDM）相比，实现复杂度相对较高，因而在实际系统中很少采用。因此，与传统的单载波系统和CDMA系统相比，正交频分复用（OFDM）系统的主要优势在于：
1） 可以有效地对抗多径传播所造成的符号间干扰，与其他实现方法相比，多载波系统实现复杂度较低；
2） 在变化相对较慢的信道上，多载波系统可以根据每个子载波的信噪比来优化分配每个子载波上传送的信息比特，从而大大提高系统传输信息的容量；
3） 多载波系统可以有效地对抗窄带干扰，因为这种干扰仅仅影响系统的一小部分子载波；
4） 在广播应用中，利用多载波系统可以实现非常具有吸引力的单频网络。
1.3.2 正交频分复用（OFDM）的不足之处
在与传统的单载波传输系统相比，正交频分复用（OFDM）系统的主要缺点在于：
1） 对于载波频率偏移和定时误差的敏感程度比单载波系统要高；
2） 多载波系统中的信号存在较高的峰值平均功率比（PAR）使得它对放大器的线性要求很高。
1.4 多载波技术的发展
多载波调制技术本质上是一种频分复用技术。频分复用技术早在19世纪以前就已经被提出，它把可用带宽分成若干相互间隔的子频带，同时分别传送一路低速信号（如电报），从而达到信号复用的目的。各子载波上的被调制数据可以来自同一信号源，也可以来自不同信号源。这种传统的多载波调制方式复杂性比较高，因为各子载波都需要自己的模拟前端，同时为了使得接收机可以区分各子频带，各子频带之间必须有足够的间隔，从而避免经过信道后发生频谱混叠，所以频谱效率通常很低。但是在这种并行传输机制下，因为各载波上的数据速率较低，相应的信号的码元符号周期较长，并远大于信道的最大时延扩展，从而可以有效地减少由于信道单位时延扩展引起的符号间干扰问题。
为了提高FDM技术的频谱利用率，G.A.Doelz等在20世纪50年代提出了Kineplex系统。该系统的设计目标是在严重多径衰落高频无线信道中实现数据传输。系统使用了20个子载波，使用差分QPSK调制，且实现方式几乎和现代的OFDM一样：相邻子载波间的间隔近似等于子载波的符号速率，从而保证各子载波的频谱相互重叠，但又是正交的，于是可以大大地提高频谱利用率，但系统仍采用了传统的多载波调制系统实现方式。随后的多载波系统也是利用类似的技术提高频谱利用率。
以上系统中的子载波频谱没有经过滤波，各子载波频谱形状均为sin(kf)/f函数形式。为了限制系统频谱，R.W.Chang等分析了多载波通信系统如何使经过滤波，带限的子载波保持正交。随后S.B.Weinstein和P.M.Ebert提出了使用离散傅利叶变换（DFT）实现多载波的基带调制和解调，这样便不再对每个子载波都使用模拟前端，从而大大地降低了多载波系统的复杂度，为正交频分复用（OFDM）的演进作出了巨大的贡献。另外，Weinstein等提出了通过插入一段空白区作为保护间隔来消除符号间干扰，但这种办法不能保证信号经过色散信道后仍然保持保持正交，为此，A.Peled和A.Ruiz提出了采用循环前缀（CP）的方法保证信号经过色散信道后仍然保持各子载波间的正交性。至此，现代正交频分复用（OFDM）的概念便形成了。1985年，Cimini把正交频分复用（OFDM）的概念引入蜂窝移动通信系统，为无线正交频分复用（OFDM）系统的发展奠定了基础。
正交频分复用（OFDM）技术具有良好的抗多径能力，从而受到大量关注。目前正交频分复用（OFDM）作为核心技术已被多种有线和无线标准采纳：
1) ADSL,被广泛用于提高铜双铰电缆用户的接入能力；
2) 在无线局域网领域的IEEE802.11a,HIPERLAN-2;
3) 欧洲数字音频广播（DAB）和数字视频广播（DVB）；
4) 无线城域网标准IEEE802.16a等等。
同时，正交频分复用（OFDM）除了作为一种传输技术，还具有支持多用户接入的功能。
正因为正交频分复用（OFDM）潜在的多径对抗能力，且可以灵活地和其它接入方式结合成衍生系统，所以正交频分复用（OFDM）已被列为4G无线通信系统的可能解决方案，而受到研究者的广泛关注。
第二章 频分复用（OFDM）系统的原理
2.1 多载波调制基础
任何实际的通信信道均存在各种干扰，这些干扰限制了系统的最大传输速率。在宽带无线数字通信系统中，影响信息高速传输的主要干扰是由信道的多径效应所引起的频率选择性衰落。频率选择性衰落表现为对信号的某些频率成分衰减严重，而对其它频率成分衰减较小，造成系统性能的下降。克服频率选择性衰落的传统方法是在接收端采用均衡器或者采用直接序列扩频加Rake接收的方法，这两种方法在2G和3G蜂窝系统中都发挥了重要作用。随着信息传输速率的进一步提高，以上方法在实现复杂度和性能方面都面临许多障碍。为了克服多径信道的频率选择性衰落，一个很自然的想法就是将信道在频域上划分成多个子信道，使每一个子信道的频谱特性都近似平坦，使用多个互相独立的子信道传输信号并在接收机中予以合并，以实现信号的频率分集，这就是多载波调制的基本思想。与常规的单载波调制不同，在多载波调制中，多数的信号处理是在频域内完成的，当子信道的数目很多时，每个子信道都可以看作是一个无ISI的子信道，发送端不需要采用复杂的信号处理技术即可实现各子信道的无ISI信息传输，而且还可以根据每个子信道的衰落况来动态调整每个子信道上所传送的信息比特数。实现多载波调制的方法有多种:矢量编码方式、小波变换方式、结构化信道信号方式(SCS)【8】、滤波多音方式、以及OFDM方式等。

2.2 频分复用（OFDM）系统的技术原理
无线传输信道的一个主要特征就是多径传播，即接收机所接收到的信号是通过不同的直射、反射、折射等路径到达接收机的，这些信号的到达时间和相位都不相同。不同相位的多个信号在接收端叠加，同相叠加会使信号幅度增加，而反相叠加则会削弱信号的幅度。这样，接收信号的幅度将会发生急剧变化，从而产生衰落。同时由于多径传输，在发射端发射的一个脉冲信号，在接收端将收到多个脉冲信号，这就造成了信道的时间弥散性。这种时间弥散性会造成接收信号中的一个符号的波形会扩展到其他符号当中，造成符号间干扰【9】(ISI)。为了避免产生ISI，应该令符号宽度要远远大于无线信道的最大时延扩展。而增大符号宽度必然会使数据传输速率降低，这就给在无线信道中高速传输数据造成了困难OFDM就是为了解决在无线信道中高速传输数据而被提出的。它通过快速傅立叶反变换IFFT【10】将数据调制到多个正交子载波上，在保证总的传输速率很高的前提下，使每个子载波上数据以较低的速率传输，从而能克服ISI。
2.2.1 OFDM的基本原理
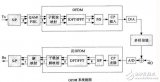
图 2.1 是OFDM系统的原理框图。编码和交织后的数据进行串/并转换为多路信号，每一路信号进行星座映射为复信号，再进行IFFT完成多载波基带调制，然后经过串/并转换后，插入保护间隔，接下来进行加窗处理及D/A转换，并进行上变频，将信号进行频带调制。在接收端信号经历了与此对反的解调过程。
图2.1 OFDM系统原理框图

2.2.2 信号映射(mapping)
这里信号映射【11】指的是一种数字调制方式，根据相应的调制编码表把每个比特组转换成一个复数。IEEE 802.11a中规定OFDM系统有四种调制方式，即BPSK,QAM,16-QAM和64-QAM。经过串/并转换的二进制数据，每一路按映射方式分为1. 2. 4或6比特一组，按BPSK,QAM,16-QAM和64-QAM的星座图映射成复数。映射是按格雷码星座图进行的，如图2.2所示。图中 表示最先输入的比特。输出值d可表示为:
(2.1)
其中， 是归一化因子，依调制方式不同而取不同的值，具体参照表2.1。乘归一化因子的目的是为了让不同映射达到相同的平均功率。例如，对于16-QAM，当输入序列为 =0010时，对照表2.1查出 ，对照表2.2查出I=-3,Q=3，由式(2.1)得到输出值d为:
(2.2)

图2.2 BPSK,QAM,16-QAM的星座图
图2.2 BPSK,QAM,16-QAM的星座图

依此类推，可以画出64-QAM的星座图(限于篇幅故不再列出)。
表2.1 不同调制方式下 的值

BPSK 1
QAM

16-QAM

64-QAM

表2.2 16－QAM映射表

输入比特（ ）

00 -3
01 -1
11 1
10 3
（ ）
输出

00 -3
01 -1
11 1
10 3

2.2.3 OFDM系统的数学模型

图2.3 OFDM系统的数学模型框图
一个OFDM符号是多个子载波的合成信号，用N表示子信道的个数，T表示OFDM
符号宽度， （i=0,1,2,…N-1）表示分配给第i个子信道的数据符号， 表示第i个子载波的载波频率，rect(t)=1, ;则从t= 开始的一个OFDM符号可以表示为:

而当t取其它值时，s(t)=0。 (2.3)
多数文献中，采用复等效基带信号【12】来描述OFDM的输出信号:
而当t取其它值时，s(t)=0。 (2.4)

上式中的实部和虚部分别对应于OFDM符号的同相分量和正交分量，在实际中可以分别与相应子载波的Cos分量和Sin分量相乘，构成最终的子信道信号和合成的OFDM符号。
图2.4 一个OFDM符号内包括的4个子载波实例

图 2.4 中给出OFDM符号内包括的4个子载波实例，每个子载波在一个OFDM符号周期内都包含整数个周期，而且相邻子载波之间相差1个周期，这一特性可以来解释子载波之间的正交性。即:

（2.5）

例如对式(2.4)第j个子载波进行解调，然后在时间长度T内进行积分，即:

＝ =
(2.6)
由上式可以看到，对第j个子载波进行解调可以恢复出期望符号 ,，而对于其他载波，在积分间隔内，频率差别(i-j)/T可以产生整数倍周期，所以其积分结果为0。

图2.5 以一个OFDM符号内包括的4个子载波为例相应的时域信号和子载波的频谱示意图（经矩形脉冲成形）

这种正交性还可以从频域角度来理解。根据式(2.3)，每个OFDM 符号在其周期T内包括多个非零的子载波。因此其频谱可以看作是周期为T的矩形脉冲的频谱与一组位于各个子载波频率上的S函数的卷积。矩形脉冲的频谱幅值为sine函数，这种函数的零点出现在频率为1/T整数倍的位置上。这种现象可以参见图2.5，其中图2.5b给出相互覆盖的各个子信道内经过矩形脉冲成形得到的sine函数频谱。在每一子载波频率的最大值处，所有其他子信道的频谱值恰好为零。由于在对OFDM 符号进行解调的过程中，需要计算每个子载波上取最大值的位置所对应的信号值，因此可以从多个相互重叠的子信道频谱中提取出每个子信道符号，而不会受到其他子信道的干扰。从图2.5可以看出，OFDM符号频谱实际上可以满足无ISI奈奎斯特准则，但传统的奈奎斯特准则是在时域上保证前后发送符号之间无干扰，此处指的是频域中各子信道间不存在干扰，这种消除ICI的方法是通过在时域中使用矩形脉冲成形，在频域中每个子载波的最大值处取样来实现。
2.2.4 用DFT实现OFDM的调制与解调
实际上，对于N比较大的系统来说，式〔2.4)中定义的OFDM 复等效基带信号可以采用离散逆傅立叶变换(IDFT)【12】来实现。
令 (k=0,1,2,…,N-1)，则可以得到:
(2.7)

上式中，s(k)即为 的IDFT运算，在接收端，可以对s(k)进行DFT变换恢复出原始数据符号 :
(2.8)
根据上述分析可以看到，OFDM 系统的调制和解调可以分别由IDFT/DFT来代替。在实际应用中，可以采用更加方便快捷的快速傅立叶变换(IFFT/FFT)【13】来实现调制和解调。N点的IDFT运算需要实施N2次的复数乘法，而IFFT可以显著地降低运算复杂度。对于常用的基2IFFT来说，其复数乘法的次数仅为(N/2)* log2(N)，而采用基4IFFT算法来实施变换，其复数乘法的数量仅为:(3 /8)*N*(log2N一2)。
2.2.5 FFT/IFFT
OFDM在调制端是通过快速傅立叶反变换【13】（IFFT)将数据调制到多个子载波上的。而在接收端则通过快速傅立叶变换 (FFT)将调制在子载波上的信号解调出来的。其调制和解调过程可用式(2.9)和式(2.10)表示为:
（ ） (2.9)
（ ） (2.10)

通过IFFT得到的多个正交子信道符号的频谱如图2.6所示。

图2.6 OFDM系统中子信道符号的频谱

由图2.6可见，各子载波频谱虽然相互重叠，但在每个子载波频率的最大值处，所有其他子信道的频谱都为零。在对OFDM符号进行解调时，只需计算每一个子载波频率的最大值，因此可以从多个相互重叠的子信道符号频谱中提取出每个子信道符号，而不会受到其他子信道的千扰。这样，也就提高了频谱的利用率。

2.2.6保护间隔和循环前缀
应用OFDM的一个主要原因是它可以有效地对抗多径时延扩展，通过把输入的数据流串/并变换到N个并行的子信道中，使得每个用于调制子载波的数据符号周期可以扩大为原始数据符号周期的N倍，时延扩展与符号周期的比值也相应降低N倍。为尽可能的消除符号间干扰，还可在每个OFDM符号之间插入保护间隔 (GI)，而且该保护间隔的时间长度一般要大于无线信道的最大时延扩展，这样一个符号的多径分量就不会对下一个符号造成干扰。在这段保护间隔内，可以不插入任何信号，即是一段空闲的传输时段。然而在这种情况中，由于多径传播的影响，不同的子载波之间会产生干扰。如图2.7所示。

图2.7 多径情况下空闲GI对子载波解调造成干扰的示意图
由于每个OFDM符号中都包括所有的非零子载波信号，而且也同时会出现该OFDM符号的时延信号，因此图2.7中给出了第1子载波和第2子载波的延时信号。从图中可以看到，在FFT运算时间长度内，第1子载波与带有时延的第2子载波之间的周期个数之差不再是整数，所以当接收机试图对第1子载波进行解调时，第2子载波会对解调造成干扰。同样，当接收机对第2子载波进行解调时，也会存在来自第1子载波的干扰。为了消除由于多径传播造成的ICI，一种有效的方法是将原来宽度为T的OFDM符号进行周期扩展，如图2.7所示。将保护间隔内(持续时间用Tg表示)的信号称为循环前缀 (Cyclic Prefix,CP )。由图中可以看出，循环前缀中的信号与OFDM符号尾部宽度为Tg的部分相同。在实际系统中，OFDM 符号在送入信道之前，首先要加入循环前缀，然后送入信道进行传送。在接收端，首先将接收符号开始的宽度为Tg的部分丢弃，然后将剩余的宽度为T的部分进行傅立叶变换解调。在OFDM符号内加入循环前缀可以保证在一个FFT积分区间内，各子载波的周期个数之差仍是整数，这样，时延小于Tg的时延信号就不会在解调过程中产生ICI.

图2.8 循环前缀的插入过程示意图
这种保护间隔是一种循环复制，增加了符号的波形长度，在交接点没有任何的间断。
因此，在OFDM系统中，CP主要有两个作用:
(1)作为保护间隔，减少了ISI;
(2 )保持各子载波的正交性，减小了ICI；
与此同时，加入CP后会带来一定的能量损失，功率损失可以定义为:
(2.11)
可见，CP越长，能量损失越大。
2.2.7 交织
交织的目的是在时域或频域或同时在时域频域上分布发射比特，以便在解调后获得理想的误码分布。获得一个理想的误码分布取决于采用的前向纠错码(FEC)，而需要什么样的交织模式取决于信道特性。如果系统在一个纯粹的AWGN环境下运行，就不需要交织，这是因为通过重新分配位的方法是无法改变误码分布的。通信信道分为快衰落和慢衰落两种信道，如果信道的冲击响应的变化与通信系统的符号速率相当时这个信道就是快衰落信道，而在慢衰落信道中，冲击响应在几个符号上都保持不变。
2.2.8 OFDM的同步技术
同步在通信系统中占据非常重要的地位，其性能直接关系到整个通信系统的性能。在OFDM系统中主要考虑三部分同步:符号同步、样值同步和载波同步，如图2.9所示。

图2.9 OFDM系统内的同步示意图
符号同步就是确定OFDM符号的起始位置，即每个FFT窗的位置。如果符号同步的起始位置在循环前缀长度内，载波间的正交性仍然保持，在这种情况下，符号同步的偏差可以看作是由信道引入的相位旋转，而这一旋转角度可由信道均衡器来求出:如果符号同步的偏差超过了保护间隔，就会引入载波间干扰。子载波的频率越高，旋转角度就越大，因此在频带的边缘，相位的旋转最大。样值同步是指接收端和发射端的抽样频率要一致。如果在样值定时中存在偏差，则会有两方面的影响:一是产生时变的定时偏差，导致接收机必须要跟踪时变的相位变化;二是样值频率的偏差就意味着FFT周期的偏差，因此经过抽样的子载波之间不再保持正交性，从而产生ICI。但幸运的是，这种影响比较小。载波同步是指接收端的振荡频率要与发送载波同频同相。由于OFDM各子信道带宽较小，对载波频率偏差的敏感程度非常高，因此需要非常精确的载波同步。频率偏移是由收发设备的本地载频之间的偏差、信道的多普勒频移等引起的，由子载波间隔的整数倍偏移和子载波间隔的小数倍偏移构成。子载波间隔的整数倍偏移仅使信息符号在子信道上平移，并不破坏各子载波间的正交性，不会引起ICI，但它却导致整个解调结果完全错误，系统的误码率近似为50%。子载波间隔的小数倍偏移由于抽样点不在顶点，破环了子载波之间的正交性引起了ICI，导致系统误码率下降。关于载波频率粗同步和细同步进行的顺序，一般是先粗同步再细同步。但如果以子载波之间的间隔为单位，将载波频率偏差从分成整数部分和小数部分，其中，只有小数部分影响子载波之间的正交性，而为整数倍的频率偏差只是将接收机中FFT的输出进行循环移位，那么，可在时域先进行载波细同步，估计载波频率偏差的小数部分，再在频域进行频率粗同步，估计整数倍的频率偏差。这种先细同步再粗同步的顺序安排，可先消除载波频偏小数部分引起的ICI，使随后的载波粗同步不受ICI影响。否则，ICI将严重破坏载波粗同步的性能。
2.2.9 OFDM系统的重要参数设计
从上面我们看到，一个OFDM 系统包括几个基本参数:保护间隔(循环前缀)长度、OFDM符号时间、子载波频率间隔和子载波个数〔系统带宽)。这些参数的确定是根据系统的实际应用要求进行折中选取。给定的基本参数有:系统带宽、数据比特速率和应用环境。由于应用OFDM 系统的主要目的是对抗信道多径时延扩展，首先要根据系统应用环境中的典型信道时延扩展 。选取一定时间长度的保护间隔T。为完全消除ISI，保护间隔的长度通常要大于时延扩展 ，显然，保护间隔越大，对抗信道时延扩展的稳健性越好;另外，如果使用保护间隔做符号同步，一般保护间隔要长于信道时延扩展一定的时间，以保证系统在一定的信噪比下、尽量少的OFDM 符号数量内实现同步。但由于保护间隔内不传输有效信息，浪费了系统的发送功率。为尽量减小保护间隔带来的系统功率损失，在确定保护间隔后应尽量加大OFDM有用符号时间T。但OFDM系统中子载波间隔为有用符号时间T的倒数，符号时间越长，子载波间隔越小，则OFDM系统对频率偏移越敏感，而且给定系统MB带宽所确定的子载波个数就越大。由于OFDM系统的峰均功率比(PAPR)跟系统的子载波个数成正比，对系统中放大器的线性范围要求更高，增加了系统实现的成本。因此，有用符号时间长度要权衡系统功率和系统性能进行折中选取，一般选择T=4 保证保护间隔带来的系统功率损失在20%以内。在一定的系统带宽资源下，符号时间确定后子载波个数(IFFT/FFT点数)也就相应确定，实际系统中因为考虑到对其它邻近信道的干扰，所以对系统的频谱哀减有一定要求，实际可用的子载波数通常小于IFFT/FFT点数，然后可以根据信源的信息速率要求确定子载波上的调制方式。
第三章 OFDM系统的仿真设计
要求在MATLAB平台上完成了OFDM系统仿真程序的设计。
3.1 OFDM的MATLAB仿真
3.1.1 MATLAB语言简介
从事科学研究和工程应用的人可能都注意到并为之所困扰，当我们在计算涉及矩阵运算或画图时，采用FORTRAN, C及C＋＋语言等计算机语言进行程序设计是一项很麻烦的工作。不仅需要对所利用的有关算法有深刻的了解，还需要熟练掌握所有语言的语法和编程技巧。例如对矩阵求逆这样的一种运算，首先要选择一个较好的求逆算法然后利用FORTRAN或C语言等高级语言编程来逐步的实现此算法，经过了艰巨烦琐的调试工作终于实现算法达到目的后，我们会发现，所编制的百余条甚至几百条语句仅仅是完成了一个矩阵的求逆工作，我们不免为自己的工作效率大发感叹。并不复杂的计算任务，用计算机来实现竟是如此的烦恼，面对手头要完成的研究任务，也许会产生畏惧之感。MATLAB正是为免除无数类似上述的尴尬局面而产生的。在1980年前后，美国的Cleve Moler博士在New Mexico大学讲授线性代数课程时，发现应用其他高级语言编程极为不便，便构思并开发了MATLAB(MATrix LABoratory，矩阵实验室)，它是集命令，翻译，科学计算于一身的一套交互式软件系统，经过在该大学进行了几次的试用之后，于1484年推出了该软件的正式版本。在MATLAB下，矩阵的运算变得异常的容易，后来的版本中又增添了丰富多彩的图形图象处理及多媒体功能，使得MATLAB的应用范围越来越广泛，Moler博士等一批数学家与软件专家组建了名为MathWorks的软件开发公司，专门扩展并改进MATLAB。 1990年MathWorks软件公司为MATLAB提供了新的控制系统模型图形输入与仿真工具，并定名为SIMULAB，该工具很快在控制界得到了广泛的使用。
与 C, C ++,FO RTRAN,PA SCAL和BASIC这类高级程序设计语言相比，MATLAB
不但在数学语言的表达与解释方面表现出人机交互的高度一致，而且具有作为优秀高技术计算环境所不可缺少的如下特征:
(1) 高质量，高可靠的数值计算能力。
(2) 基于向量，数组和矩阵的高级程序设计语言。
(3) 高级图形和可视化数据处理能力。
(4) 广泛解决各学科专业领域内复杂问题的能力。
(5) 拥有一个强大的非线性系统仿真工具箱一SIMULINK。
(6) 支持科学和工程计算标准的开放式，可扩充结构。
(7) 跨平台兼容。MATLAB程序直接可以映射为DSP芯片可接受的代码，大大提高了现代电子通信设备的研发速率。
目前 MATLAB已经成为国际上最为流行的软件之一，它除了传统的交互式编程之外，还提供了丰富可靠的矩阵运算、图形绘制、数据处理、图象处理、方便的Windows编程等便利工具，出现了各种以MATLAB为基础的实用工具箱，广泛地应用于自动控制、图象信号处理、生物医学工程、语音处理、雷达工程、信号分析、振动理论、时序分析与建模、化学统计学、优化设计等领域，并表现出一般高级语言难以比拟的优势。
较为常见的MATLAB工具箱主要包括:控制系统工具(controlsystemstoolbox)、系统辨识Z具箱(systemi dentificationto olbox).鲁棒控制-T具箱(robustco ntroltoolbox),多变量频率设计工(multivariablefrequencydesigntoolbox)、分析与综合工具箱(analysisan dsy nthesisto olbox)、神经网络1具箱(neuralne tworkto olbox)、最优化工具箱(optimizationtoolbox)、信号处理工具箱(signalpr ocessingto olbox)、模糊推理系统工具箱(fuzzyin ferencesy stemt oolbox)、小波分析工具箱〔waveletto olbox)、通信工具箱(communication toolbox)
MATLAB/Simulink属于一种通用的科学计算和系统仿真语言。在MATLAB/Simulink下，从数学模型到计算机仿真模型的转换非常容易。MATLAB/Simulink提供了三种方法【14】：
（1）M文件编程实现的方法:根据数学模型所建立的方程和数据参数，通过编程实现方程的表示和数值求解。其特点是灵活性好，数学关系显式地表达在程序语句中，但是仿真的直观性方面稍显欠缺，通常在仿真计算完毕之后才能看到结果。
（2）Simulink方法：可以根据数学模型建立对应的系统方框图，通过所见即所得的方式连接模块，然后选择求解方式和精度，运行仿真。其特点是直观性好，可以在仿真过程中实时的修改系统模块的参数。并能够实时的显示当前的仿真结果。而本人采用的是M文件编程实现的方法，具体情况见下。
3.1.2 正交频分复用（OFDM）仿真系统说明
我们在通过MATLAB语言进行OFDM系统仿真时，是将OFDM系统分为发送和接收两大部分来进行的，然后再通过信道模型将这两部分连接起来。程序的编程过程是按模块化来进行的，各子模块分别完成发送和接收中的一部分特定功能。最后再分别按发射机中的调制顺序和接收机中的解调顺序进行组合。各子模块在功能上相互独立，只是通过相应的接口进行连接，这样进行编程的好处在于各模块功能明确，在一定意义上相互独立，各个模块并不需要了解其他模块的具体实现过程，而只通过接口与其他模块发生联系，从而易于编程和修改，如对其中一个模块进行改动，并不需要对其他所有模块也进行大的改动，这非常符合国际上所达成共识的程序设计标准–结构化程序设计，即要求各个模块之间耦合性越弱越好，内聚性愈强愈好。下面将分别具体示出OFDM系统发送部分的结构图和接收部分的结构图：
1.发送部分的结构图如图3.1所示。
图 3.1 OFDM发送部分系统框图

由以上发送部分框图不难看出发送部分具体过程如下：首先，由随机码产生器产生二进制随即序列，接着通过信号映射器映射成I，Q，两路信号，这两路信号经过导频处理和傅利叶反变换（IFFT）变化来调制原始信号，OFDM系统可以采用的调制方式有BPSK，QAM，16－QAM,64-QAM多种调制方式，这里采用的是QAM调制方式，具体情况见以下程序。为了消除由于多径传播造成的ICI，一种有效的方法便是将原来宽度为T的OFDM符号进行周期扩展，用扩展信号来填充保护间隔，而且保护间隔的长度应大于无线信道的时延扩展，这样一个符号的多径分量才不会对下一个符号造成干扰。而保护间隔内的信号就称为循环前缀。所以调制后的信号要经过加入保护时隙和加入训练符号才能送入信道中去进行传送。
同理，由下面所示的接收部分系统图不难发现：在接收端，首先将接收符号开始的一定宽度的部分丢弃，然后将剩余的部分进行傅利叶变换（FFT），然后进行解调。
2.接收部分的结构图如图3.2所示。

图 3.2 OFDM接收部分系统框图

3.1.3 仿真程序说明
为了更好地说明以上OFDM系统原理的具体实现过程，以便使读者更好地了解OFDM系统的仿真实现方法。下面将整个仿真程序分为发送和接收两部分来分别进行说明。

1.发送部分程序说明
发送部分的程序设计流程图如图3.3所示。

图3.3发送部分程序设计流程图
发送部分仿真程序中需要说明的地方有:
(1) 参数初始化程序
仿真程序中需要初始化的参数如下:
采样频率：20MHz
包含数据的子载波数目：52个
包含数据的子载波的位置：[7:32 34:59]
包含用户数据的子载波数目：48个
导频子载波数目：4个
包含用户数据的子载波的位置：[7:11 13:25 27:32 34:39 41:53 55:59]
导频子载波的位置：[12 26 40 54]
生成导频时不同导频子载波需要乘的系数：[1:1:1:-1]
频域表示的短训练符号：
{0,0,1+j,0,0,0,-1-j,0,0,0,1+j,0,0,0,-1-j,0,0,0,-1-j,0,0,0,1+j,0,0,0, 0,0,0,0,-1-j,0,0,0,-1-j,0,0,0,1+j, 0,0,0,1+j,0,0,0,1+j,0,0,0,1+j,0,0}
频域表示的长训练符号：{1,1,-1,-1,1,1,-1,1,-1,1,1,1,1,1,1,-1,-1,1,1,-1,1,-1,1,1,1,1,0,1,-1,-1,1,1,-1,1,-1,1,-1,-1,-1,-1,-1,1,1,-1,-1,1,-1,1,-1,1,1,1,1}
产生导频的序列：{1,1,1,1,-1,-1,-1,1,-1,-1,-1,-1,1,1,-1,1,-1,-1,1,1,-1,1,1,-1,1,1,1,1,1,1,-1,1,1,1,-1,1,1,-1,-1,1,1,1,-1,1,-1,-1,-1,1,-1,1,-1,-1,1,-1,-1,1,1,1,1,1,-1,-1,1,1,-1,-1,1,-1,1,-1,1,1,-1,-1,-1,1,1,-1,-1,-1,-1,1,-1,-1,1,-1,1,1,1,1,-1,1,-1,1,-1,1,-1,-1,-1,-1,-1,1,-1,1,1,-1,1,-1,1,1,1,-1,-1,1,-1,-1,-1,1,1,1,-1,-1,-1,-1,-1,-1,-1}
以上参数是在程序设计过程中就已经预先设定好的参数，这部分参数不需要在仿真过程中进行设定或改动。还有一部分参数需要在仿真程序运行前在图形界面GUI中进行手动设定，这些参数包括:需要信号源产生倍号的长度(以8 Bytes为单位，因为6个字节刚好对应OFDM中包含用户数据的子载波的数目)、信号调制方式(BPSK, QPSK,16-QAM, 64-QAM)、产生信道模型中的信噪比SNR。手动设定这些参数的目的是为了使仿真系统更为灵活，更容易满足仿真和测试的需要。
(2) 信号源产生器程序
在发送部分仿真程序中，我们产生发送信号的方法是按照设定好的所需信号的长度，调用随机函数randn ()来产生。产生后的信号一方面发给接下去的模块，另一方面进行保存用于与接收机接收解调后的信号进行比较分析。
具体程序如下：
out = rand(1,baseband_out_length);
baseband_out1 = round(out) ;
baseband_out2 = floor(out*2) ;
baseband_out3 = ceil(out*2)-1 ;
baseband_out4 = randint(1,baseband_out_length);
% 四种生成发送的二进制序列的方法，任取一种产生要发送的二进制序列
if (baseband_out1 == baseband_out2 & baseband_out1 == baseband_out3 )
fprintf(’Transmission Sequence Generated \n \n’);
baseband_out = baseband_out1 ;
else
fprintf(’Check Code!!!!!!!!!!!!!!!!!!!!! \n \n’);
end
% 验证四种生成发送的二进制序列的方法
convert_matrix = reshape(baseband_out,bits_per_symbol,length(baseband_out)/bits_per_symbol) ;
for k = 1:(length(baseband_out)/bits_per_symbol)
modulo_baseband(k) = 0 ;
for i = 1:bits_per_symbol
modulo_baseband(k) = modulo_baseband(k) + convert_matrix(i,k)*2^(bits_per_symbol - i) ;
end
end
% 每2个比特转化为整数 0至3
% 采用’left-msb’方式
convert_matrix1 = zeros(length(baseband_out)/bits_per_symbol,bits_per_symbol);
convert_matrix1 = convert_matrix’ ;
Test_convert_matrix1 = bi2de(convert_matrix1,bits_per_symbol,’left-msb’);
Test_convert_matrix2 = bi2de(convert_matrix1,bits_per_symbol,’right-msb’);
if (modulo_baseband == Test_convert_matrix1′)
fprintf(’modulo_baseband = Test_convert_matrix1 \n\n\n’);
else if (modulo_baseband == Test_convert_matrix2′)
fprintf(’modulo_baseband = Test_convert_matrix2 \n\n\n’);
else
fprintf(’modulo_baseband ~= any Test_convert_matrix \n\n\n’);
end
end
carrier_matrix = reshape(modulo_baseband,carrier_count,symbols_per_carrier)’;
% 生成时间－载波矩阵
(3) 信号调制程序
可选的信号调制方式【15】有:BPSK，QPSK,16-QAM,64-QAR,这些调制方式的每个调制后符号所对应比特数目分别为:1, 2, 4, 6。调制后得到的是一个复数信号，实部对应I路信号，虚部对应Q路信号。
% Generate the random binary stream for transmit test
BitsTx = floor(rand(1,NumLoop*NumSubc)*2);
% Modulate (Generates QAM symbols)
% input: BitsTx(1,NumLoop*NumSubc); output: SymQAM(NumLoop,NumSubc/2)
SymQAMtmp = reshape(BitsTx,2,NumLoop*NumSubc/2).’;
SymQAMtmptmp = bi2de(SymQAMtmp,2,’left-msb’);
% 函数说明：
% bin2dec(binarystr) interprets the binary string binarystr and returns the
% equivalent decimal number.
% bi2de是把列向量的每一个元素都由2进制变为10进制
% D = BI2DE(…,MSBFLAG) uses MSBFLAG to determine the input orientation.
% MSBFLAG has two possible values, ‘right-msb’ and ‘left-msb’. Giving a
% ‘right-msb’ MSBFLAG does not change the function’s default behavior.
% Giving a ‘left-msb’ MSBFLAG flips the input orientation such that the
% MSB is on the left.
% % % D = BI2DE(…,P) converts a base P vector to a decimal value.
% % Examples:
% % >> B = [0 0 1 1; 1 0 1 0];
% % >> T = [0 1 1; 2 1 0];
% % >> D = bi2de(B) >> D = bi2de(B,’left-msb’) >> D = bi2de(T,3)
% % D = D = D =
% % 12 3 12
% % 5 10 5
% QAM modulation
% 00->-1-i,01->-1+i,10->1-i,11->1+i
% 利用查表法进行QAM星座映射
QAMTable = [-1-i -1+i 1-i 1+i];
SymQAM = QAMTable(SymQAMtmptmp+1);
(4) IFFT模块程序
由于MATLAB中有现成的IFFT函数可以调用，这给我们的编程带来了极大的方便，从而省去了编写IFFT算法的工作。输入及输出IFFT的数据都按矩阵格式存储，因此应当注意用户数据和导频数据在矩阵中的存放位置，必须按OFDM规定的格式进行存放，否则在接收端将不能正确解调。
% input: SymQAM(NumLoop,NumSubc/2); output: SymIFFT(NumSubc,NumLoop)
SymIFFT = zeros(NumSubc,NumLoop);
SymIFFTtmp = reshape(SymQAM,NumSubc/2,NumLoop);
SymIFFTtmptmp = zeros(NumSubc,NumLoop);
SymIFFTtmptmp(1,:) = real(SymIFFTtmp(1,:)); % 实数
SymIFFTtmptmp(NumSubc/2+1,:) = imag(SymIFFTtmp(1,:)); % 实数
％ 这么安排矩阵的目的是为了构造共轭对称矩阵
％ 共轭对称矩阵的特点是 在ifft/fft的矢量上 N点的矢量
％ 在0，N/2点必须是实数 一般选为0
％ 1至N/2点 与 （N/2）+1至N-1点关于N/2共轭对称
SymIFFTtmptmp(2:NumSubc/2,:) = SymIFFTtmp(2:NumSubc/2,:);
SymIFFTtmptmp((NumSubc/2+2):NumSubc,:) = flipdim(conj(SymIFFTtmp(2:NumSubc/2,:)),1);
% % >> a = [1 2 3; 4 5 6; 7 8 9; 10 11 12]
% % a =
% % 1 2 3
% % 4 5 6
% % 7 8 9
% % 10 11 12
% % >> b = flipdim(a,1)
% % b =
% % 10 11 12
% % 7 8 9
% % 4 5 6
% % 1 2 3
SymIFFT = ifft(SymIFFTtmptmp,NumSubc,1);
2.接收部分程序设计说明
接收部分的程序设计流程图如图3.4所示。

图3.4 接收部分程序设计流程图

接收部分仿真程序中需要说明的地方有:
(1) 分组检测程序
分组检测程序用于检测是否已接收到数据分组，该程序采用了Schimdl和Cox的延时和相关算法进行检测，延时D=16，也就是短训练序列的长度。用于判定分组是否到来的判定阐值设定为threshold=0.75。对于算法中的相关运算和功率计算的结果都用了filter()函数进行了滤波，从而使判断更为准确。
(2) 精确时间同步程序
虽然在分组检测程序中，Schimdl和Cox的延时和相关算法已经在一定程度上达到了粗略的时间同步，但这还不能满足正确解调的要求，因此要进行精确的时间同步。精确时间同步程序采用将己知的长训练符号和接收数据进行相关运算的方法，当运算结果大于判定阈值0.75时，判定己达到时间同步，将接收信号输出到下一模块。这里输出的数据是已经去除了前导的数据，即全部都是需要解调的数据。
(3) 频率同步程序
频率同步程序包含两个小模块，一个是频率偏移估计程序，一个频率偏移补偿程序。频率偏移估计程序采用的是时域中的频率偏移估计算法，算法中延时窗长度D=16.频率偏移补偿程序将估计出的频率偏移相位取反后，按时间向量顺序，生成相应的频率补偿向量，与原信号向量相乘达到频率偏移补偿的目的。
(4) FFT模块程序
调用MATLAB中的FFT函数进行运算，并将输出数据中的导频数据和需解调数据分开。导频数据用于相位跟踪，同时还要输出FFT运算后的长训练符号，用于信道估计。典型语句如下：
% input: SymDeCP(NumSubc,NumLoop); output: SymFFT(NumSubc,NumLoop)
SymFFT = fft(SymDeCP,NumSubc,1);
(5) 信道估算程序
进行信道估算的目的是为了载波相位跟踪。方法是通过FFT，后得到的长训练序列和已知的长训练序列进行相关运算得到。
(6) 相位跟踪模块程序
通过信道估算模块得到的信道冲击响应的估计，和FFT模块得到的频域导频信号，进行相位误差估计，得到需要补偿的相位，然后对这个相位误差进行取反后乘回到原信号中。
(7) 解调模块程序
解调应根据发射机所选的不同调制方式进行相应的解调。解调时采用的是硬判决的方式。

% SymFFT(NumSubc,NumLoop); output: SymDec(NumSubc,NumLoop)
SymDec = zeros(NumSubc,NumLoop);
SymEqtmp(1,:) = SymFFT(1,:)+i*SymFFT(NumSubc/2+1,:);
SymEqtmp(2:NumSubc/2,:) = SymFFT(2:NumSubc/2,:);
for m = 1:NumLoop
for n = 1:NumSubc/2
Real = real(SymEqtmp(n,m));
Imag = imag(SymEqtmp(n,m));

if( abs((Real -1)) < abs((Real +1)))
SymDec(2*n-1,m) = 1;
else
SymDec(2*n-1,m) = 0;
end
if( abs((Imag -1)) < abs((Imag +1 )) )
SymDec(2*n,m) = 1;
else
SymDec(2*n,m) = 0;
end
end
end
% ————————————————————————-
% Another way to DeQAM
% QAMTable = [-1-i -1+i 1-i 1+i];
% 00->-1-i,01->-1+i,10->1-i,11->1+i
TestSymDec = zeros(NumSubc,NumLoop);
TestSymEqtmp(1,:) = SymFFT(1,:)+i*SymFFT(NumSubc/2+1,:);
TestSymEqtmp(2:NumSubc/2,:) = SymFFT(2:NumSubc/2,:);
TestSymEqtmp1 = reshape(TestSymEqtmp,1,NumSubc*NumLoop/2);
min_d = zeros(size(TestSymEqtmp1));
min_ddd = zeros(1,NumSubc*NumLoop);
d = zeros(4,1);
min_index = 0;
for ii = 1:1:(NumSubc*NumLoop/2)
for jj = 1:4
d(jj) = abs(TestSymEqtmp(ii) - QAMTable(jj));
end
[min_d(ii),min_index] = min(d);
% % [Y,I] = MIN(X) returns the indices of the minimum values in vector I.
switch min_index
case 1
min_ddd(2*ii-1) = 0 ;
min_ddd(2*ii) = 0 ;
case 2
min_ddd(2*ii-1) = 0 ;
min_ddd(2*ii) = 1 ;
case 3
min_ddd(2*ii-1) = 1 ;
min_ddd(2*ii) = 0 ;
case 4
min_ddd(2*ii-1) = 1 ;
min_ddd(2*ii) = 1 ;
otherwise
fprintf(’Impossible error!!! \n\n’);
end
end
%————————————————————————–
% 函数说明：
% % C = min(A) returns the smallest elements along different dimensions of an array.
% % If A is a vector, min(A) returns the smallest element in A.
% % If A is a matrix, min(A) treats the columns of A as vectors, returning a row
% % vector containing the minimum element from each column.
% % [C,I] = min(…) finds the indices of the minimum values of A, and returns
% % them in output vector I. If there are several identical minimum values, the
% % index of the first one found is returned.
% Bit Error
BitsRx = zeros(1,NumSubc*NumLoop);
BitsRx = SymDec(:).’;
[Num,Ber] = symerr(BitsTx,BitsRx)
BerSnrTable(snr+1,2) = Num ;
BerSnrTable(snr+1,3) = Ber ;
end
%————————————————————————–
if min_ddd == BitsRx
fprintf(’DeQAM two ways the same results \n\n’);
else
fprintf(’DeQAM two ways the different results’);
end
% ————————————————————————
figure(1);
subplot(2,1,1);
semilogy(BerSnrTable(:,1),BerSnrTable(:,2),’o-’);
subplot(2,1,2);
semilogy(BerSnrTable(:,1),BerSnrTable(:,3),’o-’);
% ————————————————————————
time_of_sim = toc
3.1.4 调试过程和结果分析
本人是用MATLAB的M文件来实现正交频分复用（OFDM）系统的仿真的，具体调试运行过程如下：首先将事先编制好的程序放入MATLAB6.5中去编译运行，得出最终的仿真结果（OFDM系统的信噪比与误码率曲线图）如下所示：

图3.1 OFDM系统的信噪比与误码率曲线图
由上图不难看出OFDM系统的误码率随着信噪比的增加而减少。（注意：横坐标为信噪比，单位（dB）;纵坐标为误码率，信道为加性白高斯噪声信道）
第四章 结束语
4.1总结
OFDM作为一种先进的通信技术，由于其具有的高效频谱利用率和优良的抗多
径千扰能力，从它面世开始，就引起了众多研究人员的关注。伴随着半导体技术
和数字信号处理技术的不断进步，结合了现代最前沿数字信号处理成就的OFDM
技术的大规模应用己经成为趋势。
研究一种新技术，必然会结合它的应用领域，从而才能较有深度地发现新技术的特点和发掘新技术的潜力。本文从OFDM技术应用较多的场合之一的无线通信领域入手，系统地介绍了OFDM技术应用的场合，提出了OFDM技术的概念，介绍了它的发展历史和基本原理，并分析比较了传统和现代的不同系统实现方法，初步认识了OFDM技术得到广泛应用的原因。
本文的主体部分主要包括两方面:系统原理阐述和系统实现方案。在初步了解OFDM技术基本原理的基础上，在系统原理阐述部分，本文系统详细地介绍了OFDM系统实现中涉及到的关键技术环节，这部分内容基本上涵概了OFDM系统实现中所包含的主要技术关键点和难点，使得OFDM系统作为一个完整的体系，得到了充分的论述。OFDM技术作为一种先进而又复杂的技术，其系统实现中涉及到了众多领域知识，分析比较这些关键技术对OFDM系统性能的贡献，是在系统实现方案提出之前的一项必须工作。本文通过利用Matlab数学工具，对OFDM系统在抗加性高斯白噪声这方面进行了仿真，得出了OFDM系统的信噪比－误码率曲线图，进而得出OFDM技术在这个方面的优良性能，知道了OFDM技术能够在众多领域得到充分利用的原因，也使得系统方案的提出有了理论上的保证。同时，本文还进行了OFDM系统中的信号映射子模块，信号调制和解调子模块，以及简单信道估计的仿真研究。在此基础上分析了OFDM系统的优缺点，并简要概述了OFDM应用的关键技术之一–信道估计技术。本文主要研究了单一的信道估计方法（LMS信道估计），得出了在不同信噪比下对不同误码率的研究，对于信道估计人们提出了很多方法，需要进行进一步的研究和论证，根据实际应用背景找出最适合的解决方案。
4.2不足与展望
通过本论文的创作，希望能在知识的积累之外，获得严谨的治学态度及科学
的精神。并期望在本文的基础上做出更大的成绩。论文尚有许多不足之处，例如：在信道估计方面可以加入几种不同信道估计算法之间的对比（比如与LS算法，MMSE算法之间的对比），同时最好能有这方面的图形界面显示出来，我相信如果用SIMULINK来做应该会更好些。衷心恳请诸位老师和朋友阅后不吝赐教。
未来的无线OFDM系统中研究工作可以从以下方面展开:
1. 对于无线OFDM系统中信道盲估计算法，需要解决的问题是如何加快算法的收敛速度、减小进行信道盲估计时所需的数据量、增加跟踪时变信道的OFDM通信系统中信道估计算法研究能力以及提高其盲估计算法的性能。
2. 将基于训练序列的信道估计方法与盲信道估计方法结合起来，研究收敛
速度快、性能优越的半盲信道估计方法。
3. 目前无线OFDM系统中新的研究方向就是基于多天线OFDM系统，即MIMO-OFDM系统。多天线技术可以有效地改善系统容量及性能，而且还可以显著地提高网络的覆盖范围和可靠性。MIMO-OFDM系统内的关键技术包括发送分集、空间复用、接收分集和干扰消除、软译码、信道估计、同步和自适应调制和编码。