Web文档聚类中k-means算法的改进
介绍了Web文档聚类中普遍使用的、基于分割的k-means算法,分析了k-means算法所使用的向量空间模型和基于距离的相似性度量的局限性,从而提出了一种改善向量空间模型以及相似性度量的方法。
关键词: 文档聚类 k-means算法 向量空间模型 相似性度量
Internet的快速发展使得Web上电子文档资源在几年间呈爆炸式增长,与数据库中结构化的信息相比,非结构化的Web文档信息更加丰富和繁杂。如何充分有效地利用Web上丰富的文档资源,使用户能够快速有效地找到需要的信息已经成为迫切需要解决的问题。
聚类能够在没有训练样本的条件下自动产生聚类模型。作为数据挖掘的一种重要手段,聚类在Web文档的信息挖掘中也起着非常重要的作用。文档聚类是将文档集合分成若干个簇,要求簇内文档内容的相似性尽可能大,而簇之间文档的相似性尽可能小。文档聚类可以揭示文档集合的内在结构,发现新的信息,因此广泛应用于文本挖掘与信息检索等方面。
文档聚类算法一般分为分层和分割二种,普遍采用的是基于分割的k-means算法。
k-means算法具有可伸缩性和效率极高的优点,从而被广泛地应用于大文档集的处理。针对k-means算法的缺点,许多文献提出了改进方法,但是这些改进大多以牺牲效率为代价,且只对算法的某一方面进行优化,从而使执行代价很高。
k-means算法中文档表示模型采用向量空间模型(VSM),其中的词条权重评价函数用TF*IDF表示。然而实际上这种表示方法只体现了该词条是否出现以及出现多少次的信息,而没有考虑对于该词条在文档中出现的位置及不同位置对文档内容的决定程度不同这一情况。另一方面,k-means算法使用基于距离的相似性度量,然而文档的特征向量一般超过万维,有时可达到数十万维,这种高维度使得这种度量方法不再有效。针对以上问题,本文提出相应的解决方法,即改进的k-means算法。实验表明改进后的k-means算法不仅保留了原算法效率高的优点,而且聚类的平均准确度有了较大提高。
1 k-means算法简介
k-means算法是一种基于分割的聚类算法。基于分割的聚类算法可以简单描述为:对一个对象集合构造一个划分,形成k个簇,使得评价函数最优。不同的评价函数将产生不同的聚类结果,k-means算法通常使用的评价函数为:
k-means算法的具体过程如下:
(1)选取k个对象作为初始的聚类种子;
(2)根据聚类种子的值,将每个对象重新赋给最相似的簇;
(3)重新计算每个簇中对象的平均值,用此平均值作为新的聚类种子;
(4)重复执行(2)、(3)步,直到各个簇不再发生变化。
k-means算法的复杂度为:O(nkt)。其中:n为对象个数,k为聚类数,t为迭代次数。通常k、t<< n,所以k-means算法具有很高的效率。同时k-means算法具有较强的可伸缩性,除了生成k个聚类外,还生成每个聚类的中心,因此被广泛应用。
2 k-means算法的分析及其改进
2.1 权重评价函数的改进
k-means算法采用向量空间模型(VSM)将Web文档分解为由词条特征构成的向量,利用特征词条及其权重表示文档信息。向量d=(ω1,ω2,ω3,∧,ωm)表示文档d的特征词条及相应权重。其中:m为文档集中词条的数目,ωi(i=1,∧,m)表示词条ti在文档d中的权重。特征权重ωi的计算通常采用经典的TF*IDF算法,并进行规格化处理:
其中:TF表示该词条ti在文档d中的频数,DFi表示文档集中包含词条ti的文档数,N表示文档集中的文档数。从公式(2)可以看出,这种特征权重的计算方法是把文档当做一组无序词条,词条特征权重只是体现了该词条是否出现以及出现次数多少的信息,而对于词条在文档中的不同位置对文档内容的决定程度不同这一问题却未加考虑。
对于Web文档而言,由于XML(可扩展标识语言)已经成为Web上新一代数据内容描述标准,因此Web上的文档聚类应体现XML文档的特性。XML文档中的基本单位是元素(element)。元素由起始标签、元素的文本内容和结束标签组成。它的语法格式为:
<标签> 文本内容
基于XML的Web文档中,用户把要描述的数据对象放在起始标签和结束标签之间,无论文本的内容多长或者多么复杂,XML都可以通过元素的嵌套进行处理。不同标签下,同一个词条也可能有不同含义。由此可见,XML文档中不同位置的词条对文档内容的决定程度会有很大的不同。
通常,一个文档的标题、摘要、关键词以及段首和段尾出现的词条对整个文档内容有很大的决定作用。在XML文档中,通过标签可以得出词条对文档内容的决定程度,但很难对这种决定程度进行准确的定义。因此,本文利用模糊集理论,根据XML文档特性计算词条从属关系系数,并且将其量化为介于0和1之间的隶属度,加入到原有权重评价函数,从而表明XML文档具有该词条特征的程度。
为了简化计算,词条在文档中出现的位置主要分为标题、摘要、关键词、段首尾、特殊标识处和正文几个部分。其相应权重为σt,在[0,1]之间取值,用lt表示词条在相应位置出现的次数。加入了词条隶属度的权重评价函数为:
2.2 相似性度量的改进
利用向量空间模型处理Web文档时,由于文档的繁杂性,表示文档的特征向量可以达到数万维,甚至更多。通过预处理阶段停用词和无用高频词的过滤后,特征向量的维数虽然显著减少,但剩余的维数仍然很多。本文实验中选用的娱乐类1500篇Web文档在预处理后特征向量的维数仍然达到了8291维。
如此高维的特征向量使得聚类算法的处理时间大大增加,同时对算法的准确性产生不利影响,并且这些特征对于聚类来说大多是无用的,例如聚类算法STC(Suffix Tree Clustering)将特征向量的维数减少到几十维仍然能够准确聚类。这主要是因为,对于非结构化的文档,体现其类别特点的特征词有很多,当进行某一方面的聚类时,与此无关的特征词就成了噪音。从这一点来说,文中前面改进的权重评价函数 体现了特征词对文档内容的贡献程度,从而突出了与聚类相关的特征词,降低了无关特征词的干扰。另一方面,过多的特征词使得特定的特征词出现的频率较低,容易被噪音所淹没。
体现了特征词对文档内容的贡献程度,从而突出了与聚类相关的特征词,降低了无关特征词的干扰。另一方面,过多的特征词使得特定的特征词出现的频率较低,容易被噪音所淹没。
k-means算法使用基于距离的相似性度量,通过计算文档向量之间的距离表明文档之间相似性的大小。通常采用的是余弦函数,计算公式为:
利用向量空间模型对文档进行聚类只能根据文档的二种信息:(1)文档中每个特征词出现的频率;(2)文档的长度。由于文档长度与文档所属的类别之间的关系不大,因此可以把所有的文档长度进行归一化处理,从而使文档向量具有统一的特征维数m。
其中:m为特征向量维数,αk为二个文档对应特征词条的四位码字的十进制数值差的绝对值。由于这种相似性的计算使用的是整数,所以计算速度和精度得到一定的提高。
可以利用简单的示例验证公式(5)的合理性。当二个文档完全相似时,sim(di,dj)的值等于1,而二个文档完全不同时它的值为0。这种方法不仅反应了文档之间的差异,而且定量地描述了这种差异性,从而为文档的聚类提供了依据。下面通过对具体的Web文档进行实验并进一步地验证。
3 实 验
实验用的文档是从搜狐的中文网站上获取的娱乐类文档,选用其中的1500篇。对这1500篇文档进行手工分类,如表1所示共分为10类。
衡量信息检索性能的召回率和精度也是衡量分类算法效果的常用指标。然而聚类过程中并不存在自动分类类别与手工分类类别确定的一一对应关系,因此无法像分类一样直接以精度和召回率作为评价标准。为此本文选择了平均准确率作为评价的标准。平均准确率通过考察任意二篇文章之间类属关系是否一致来评价聚类的效果。
试验中对使用公式(3)和(5)的改进k-means算法和原k-means算法的平均准确度进行了比较,实验结果如表2所示。
实验结果表明,改进后的k-means算法与原k-means算法在运行速度上基本相同甚至略快,平均准确度则比原算法有了普遍提高,尤其在正确指定聚类数k时,平均准确度提高了近7%,说明此算法具有较高的准确性。由于实验中使用的文档集很小,所以改进的算法优势不很明显。
4 结束语
本文对k-means算法进行了改进。根据不同位置的特征词条对文档内容的不同决定程度,提出一种新的文档特征词条的权重评价函数,并在此基础上提出一种文档相似性的度量方法。实验表明改进后的算法不仅保留了原k-means算法效率高的优点,而且在平均准确度方面比原算法有了较大提高。实验还表明,k-means算法要依赖原始聚类数k的选择。如何为初始文档集选择合适的聚类数k以及进一步提高平均准确度是今后改进k-means算法的主要研究方向。
参考文献
1 Fraley C,Raftery A E.How Many Clusters?Which ClusteringMethod?Answers Via Model-Based Cluster Analysis.
Department of Statistics University of Washington Technical Report,1998
2 Xu L.How Many Clustering?:A YING-YANG Machine Based Theory For A Classical Open Problem In Pattern Recognition. IEEE Trans,Neural Networks,1996;3(10)
3 Jiang M F,Tseng S S,Su C M.Two-phase clustering process for outliers detection.Pattern Recognition Letters,2001;(22)(6~7)
4 Michaud P.Clustering techniques.Future Generation Computer System,1997;13(6)
5 Pedrycz W,Bagiela A.Granular Clustering:A Granular Signature of Data.IEEE Trans,Neural Networks,2002;32(2)
 电子发烧友App
电子发烧友App







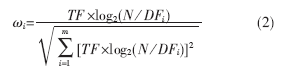






























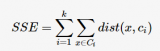










评论