DSP在电能表中的应用 - 全文

      实时数字信号处理、超大规模集成电路技术的飞速发展，不断地推动着数字信号处理器性能的提高，使其在信号处理、军事及民用电子技术领域发挥着越来越重要的作用，其应用广度和深度也在不断地扩展和深化。数字信号处理相对于模拟信号处理有很大的优越性，主要表现在精度高、灵活性强、可靠性好、易于大规模集成及存储等方面，而且可以采用多种性能优良的数字信号处理方法和算法。实时数字信号处理技术的核心和标志是数字信号处理器。快速傅里叶变换等实用算法的提出，促进了实现数字信号处理的发展。数字信号处理在于运算处理的实时性。

       电能表作为电能的计量工具，多年来一直倍受国家电力部门的重视，电能表生产企业更是不遗余力地致力于设计与开发，但目前我国电能表设计水平仍比较落后，高精度电能表主要依靠进口,传统的4位、8位单片机因为自身性能的局限，在高精度电能计量方面难免捉襟见肘，而DSP技术在电能表中的应用为电能计量精度的大幅度提高带来了新的希望。

  &nbs 
p;    DSP在电能表中的应用

       根据电能表的功能和误差精度的需求，我们选用了TI公司的TMS320VC5402芯片，在程序设计上除了完成快速数据处理工作以外，还针对系统非线性失真进行了修正和补偿。

       采集数据处理与计算

       在实际应用中，电力信号通过互感器采集到电能表中，通过一个6通道16位模拟输入前端处理器（AD73360）进行（A/D）模数转换，变成数字信号并传输到DSP中，然后对采样的数据进行数字滤波。在DSP中应用采样技术需要快速ADC，即以非常快的速度来采样模拟信号，并且需要快速DSP来执行数字低通滤波和抽取。在数字信号处理中，滤波占极其重要的作用，它解决了模拟滤波器无法克服的电压漂移、温度漂移和噪声等问题，从而改善了数字信号的跳动，使得电压电流信号的波形趋于理想状态。电能表原理框图示于图1。

 

图 1   电能表的原理框图

       在采样过程中，首要的问题是采样频率的选择，Nyquist采样定理指出：若连续信号x（t）是有限带宽的，其频谱的最高频率为fc，对x（t）采样时，若保证采样频率fs≥2fc，那么，就可由采样信号恢复出x（t）。在实际对x（t）作采样时，首先要了解x（t）的最高截止频率fc，以确定应选取的采样频率fs。若x（t）不是有限带宽的，在采样前应使用抗混叠（anti－aliasing）滤波器对x（t）作模拟滤波，以去掉f＞fc的高频成分。因此，在A/D转换前就需要模拟低通滤波器具有尖锐的滚降特性，来限制模拟信号的频谱。一个理想的滤波器应能让所有低于fs／2的频率通过，而完全阻隔掉所有大于fs／2的频率。通常，滤波器和采样频率的选择是将我们感兴趣的频带限制在DC和fs／2之间。

       首先对电压电流输入信号进行数据采样和RC滤波网络滤波，然后进行A/D转换。A/D转换完成后产生中断，在中断服务子程序中读出每次转换的结果，作为数字低通滤波的输入。DSP的输入是A/D转换后得到的数字信号，DSP对输入的数字信号进行处理，并经过一定的计算和转换得到相应的能量。在DSP处理器中是按以下式进行运算的：

       * 电压测量(有效值)计算式：

       式中：U－电压有效值，n－每周期采样点数，－电压采样值。

       * 电流测量(有效值)计算式

       式中：I－电流有效值，n－每周期采样点数，－电流采样值。

       * 单元件有功功率计算式

       式中： P－单元件有功功率，n－每周期采样点数，－元件上电压采样值，－元件上电流采样值。

       * 单元件无功功率计算式

      式中：Q－单元件无功功率，n－每周期采样点数，－元件上电压采样值，－元件上电流采样值(移相后)。

       * 三相四线三元件有功功率计算式：

       式中：－三相有功功率，－(i=A,B,C)各相有功功率。

       *三相四线三元件有功功率计算式：

       式中：－三相无功功率，－(i=A,B,C)各相无功功率。

       数字滤波的设计

       数字滤波器运算结构的不同，将会影响系统运算的精度、误差、速度和经济性等性能指标。在一般情况下，都要求使用尽可能少的常数乘法器和延迟器来实现系统，并要求 
运算误差尽可能小。我们主要采用FIR结构的滑动平均滤波器（MovingAverage Filter)。

       在数字信号处理应用中往往需要设计线性相位的滤波器，FIR滤波器在保证幅度特性满足技术要求的同时，很容易做到严格的线性相位特性。为了使滤波器满足线性相位条件，要求其单位脉冲响应h(n)为实序列，且满足偶对称和奇对称条件，即h(n)=h(N-1-n)和h(n)=-h(N-1-n)。

       由此可见，FIR滤波器不断地对输入样本x(n)延时后，再作乘法累加算法，将滤波结果y(n)输出，因此，FIR实际上是一种乘法累加运算器。在数字滤波器中，FIR滤波器的最主要特点是没有反馈回路，故不存在不稳定的问题；同时，可以在幅度特性随意设置的同时，保证精确、严格的线性相位。稳定和线性相位特性是FIR滤波器的突出优点。下面是FIR滤波器设计的子程序:

.TEXT
   BEGIN     LDP  80H,DP
      LDI  @STACK_ADDR,SP
      LDI  21,BK
      LDI  19,RC
      LDI  @XN_ADDR,AR1
      LDI  @XNNEW_ADDR,AR2
      LDI  @OUTNEW_ADDR,AR3
   LOOP      LDF  *AR2,R6
      STF  R6,*AR1++(1)%
      LDI  @HN_ADDR,AR0
      CALL  FIR
      STF  RO,*AR3
      BR      LOOP

       数据处理方式

       数据处理主要是对采集的离散化信号进行运算处理，利用快速傅里叶算法对电信号进行分析（参图 2所示）。

 

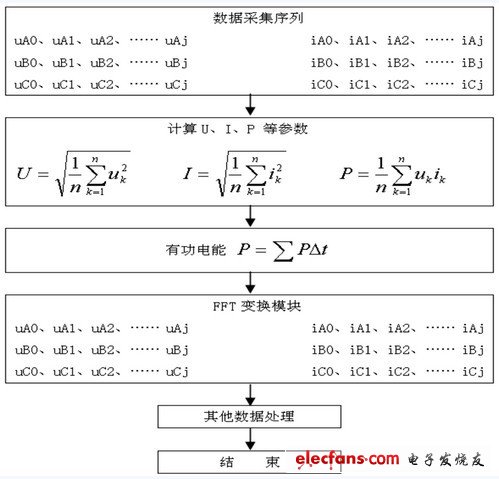
图2  数据处理

       在DSP中最常用的方法是频域分析法。对于一些序列长度小的，通常采用离散傅里叶变换(DFT的精确定义为:X(m)=)，而序列长度大的，通常采用快速傅里叶变换(FFT)。FFT的运算速度要比DFT的运算速度快得多，但DFT的灵活性比较强。如果需要求出少量的频域值，DFT方法可以比FFT运算量小，数据序列长度可以是任意的，并且N个输出值的计算是相互独立的。由于DFT的输出是复数，所以实部和虚部包含在两个N长度的数组中，对于输出的结果可以通过计算机软件(MATLAB)进行仿真。计算和绘制DFT的输出结果，通过FFT在DSP中的应用，计算出N次谐波分量，从而提高了电能表上的各种技术参数。