DNN加速器的设计一直在两个方面使力:通用架构和高效性能。通用性需要自顶向下的设计,首先综合各种神经网络的算子设计一套标准的指令集,然后根据硬件平台的特点,考察计算资源,存储资源以及带宽,进行硬件的模块化设计,在指令集以及硬件的特殊结构基础上,再去构建工具链。
通用性要看的广,指令集的定义要具有扩展性和灵活性,工具链要能够灵活的对接不同的深度学习框架,能够处理不同类型的网络。这是一个很大的工程,需要一个顶级架构师以及大批软件编译类工程师合力来做。但是现在出现的很多开源工具链框架将这种开发难度大大降低了,比如TVM,LLVM,MLIR等工具给我们提供了基础,避免了再造轮子的重负。很多公司也基于这些开源框架来编写自己的编译工具。
高效性能永远是各大芯片厂商比拼的焦点,性能的提升需要三个方面共同努力:一个是来自于芯片的广大的资源,包括计算资源和存储资源,以及高带宽,从Xilinx芯片不断加大尺寸和DSP数量,以及采用HBM,还有GPU内核数量的提升以及对HBM的采用都说明了这个问题;另外一个是算法的深度优化,神经网络对噪声的容纳能力让其有了很多可以利用的空间,比如int类型的量化,稀疏化,剪枝等等,可以在保证精度的前提下,大大降低其运算量以及参数数量,同时能够更好的适配硬件;第三就是需要编译器对指令的优化,算符融合,无效算子的kill,指令的schedule等等,都会对最后性能造成很深的影响。提升性能需要看的深,追求硬件,算法,编译的极限,尽最大可能利用硬件有限的资源,尽最大可能优化网络的结构,尽最大可能寻求指令序列的优化解。今天我们谈性能追求当中的一个很小的部分——DSP。
Xilinx DSP
1 结构和功能
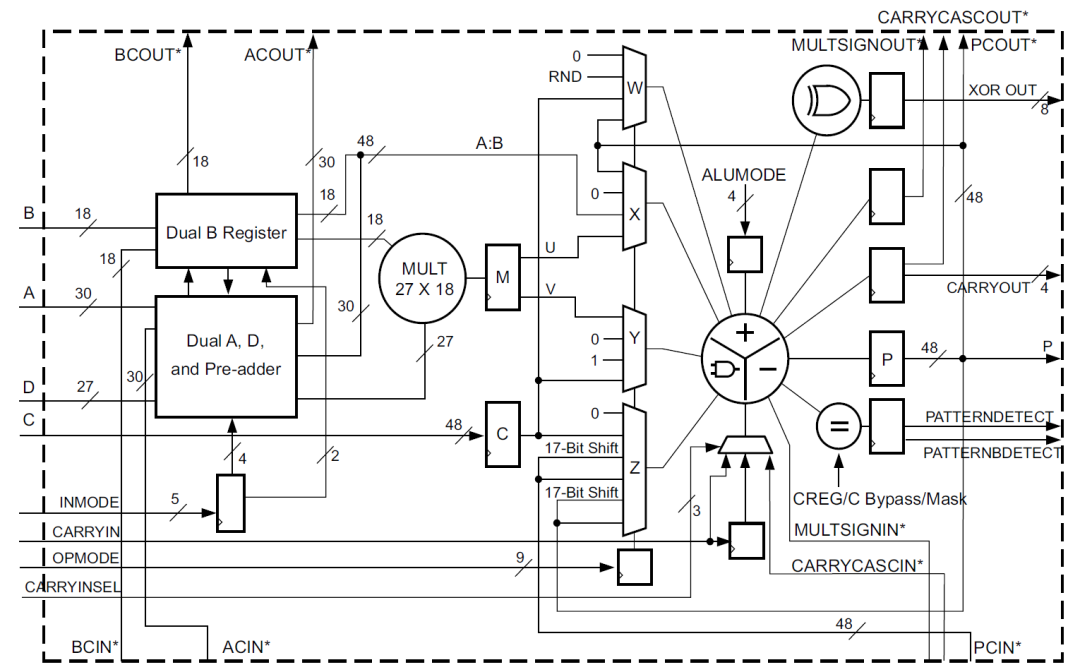
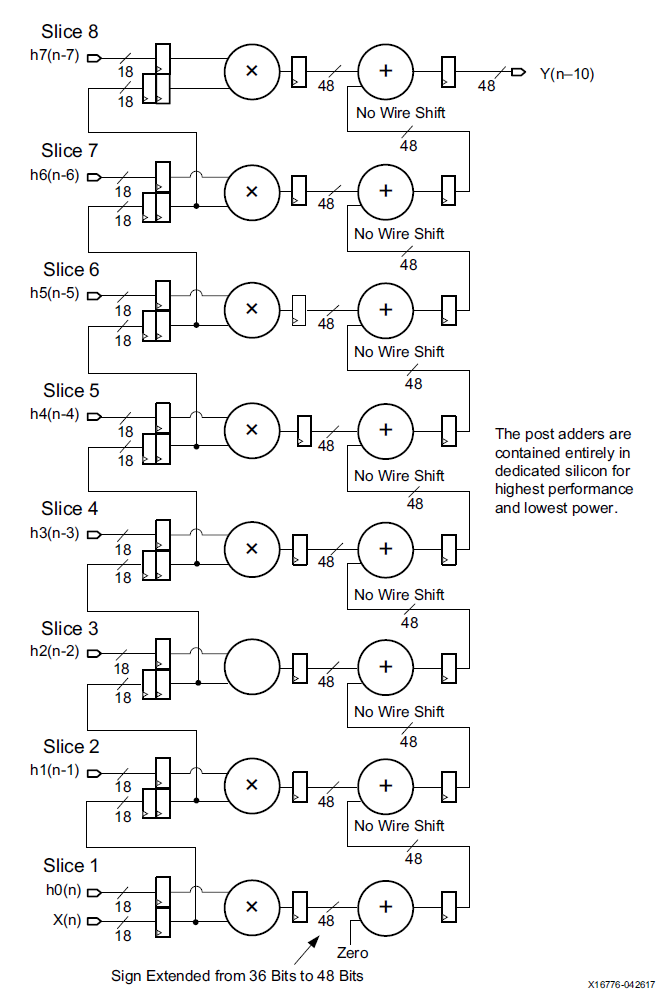
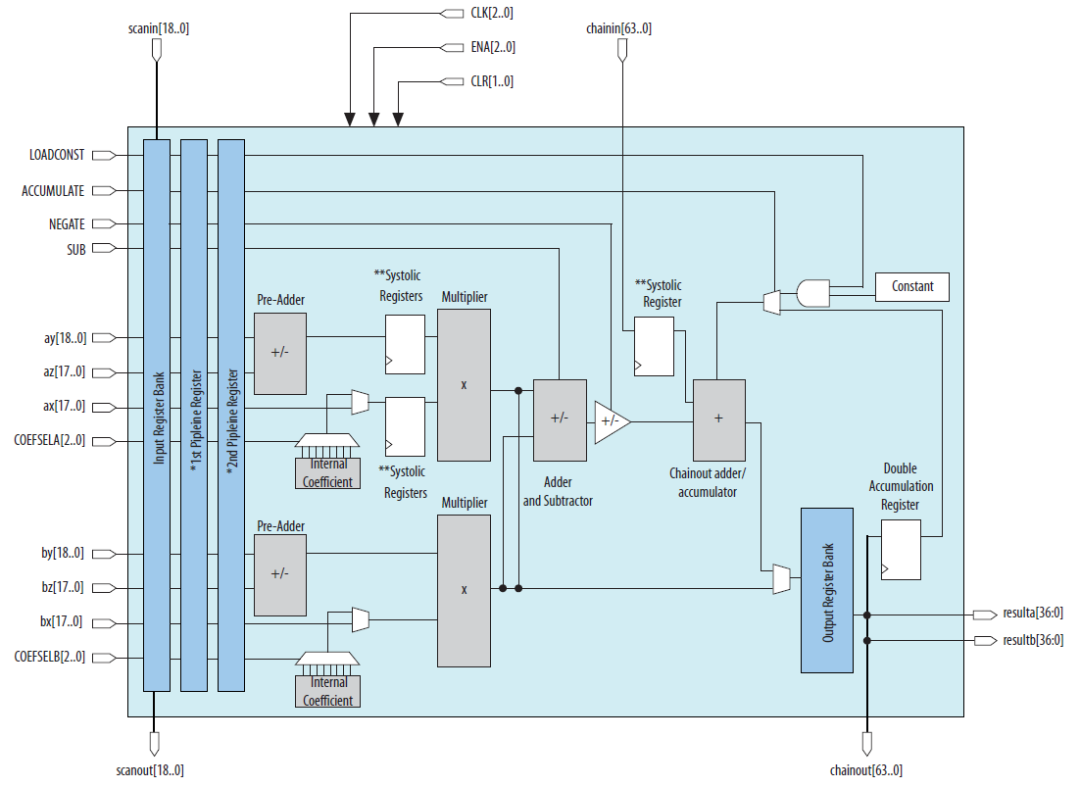
DSP48E2是zynq器件中使用的DSP类型,其主要结构包括一个27bit前加器,27x18bit的乘法器,一个48bit的可以执行加减法,累加以及逻辑功能的ALU。如下图所示:
DSP48E2单元的功能包括:
1) 前加器可以计算D+/-A以及D+/-B的功能,这大大扩展了A和B端口的公用。通过对A和B的选择,可以增加乘数的宽度,利用这个可以将神经网络的算力提高一倍甚至两倍,后边我们具体再讲。
2) 前加器可以将结果发送到乘法器,所以提供了平方操作,比如A*A。
3) A端口的低27bit用于乘法器输入,30bit完整数据可以和B端口数据concate实现48bit数据的ALU操作,包括与或非等逻辑运算以及加减法计算。
4) 端口CARRYCASCIN和CARRYCASCOUT能够用于多个DSP级联,这对于实现神经网络中的矩阵乘法或者卷积的累加非常方便。
5) 基于SIMD模式的加减法操作,可以支持2路24bit加减法以及4路12bit加减法。
6) 支持48bit的逻辑操作:and, or, not, nand, nor以及xnor。
7) 支持一些类型检测:overflow/underflow,rounding等。
8) 支持17bit右移操作。
9) DSP单元是单时钟同步运转的,始终频率能够达到内部memory频率的两倍,相对内部逻辑,DSP可以工作在倍频下。
DSP支持的操作类型很多,主要用于两方面:一个是基于大量乘累加的计算,比如conv,gemm,FFT等。另外一种是纯加减法和逻辑的运算,这些在神经网络中也有很多,比如element-wise add。逻辑运算用的不多,更多可能作为一些计算的辅助。
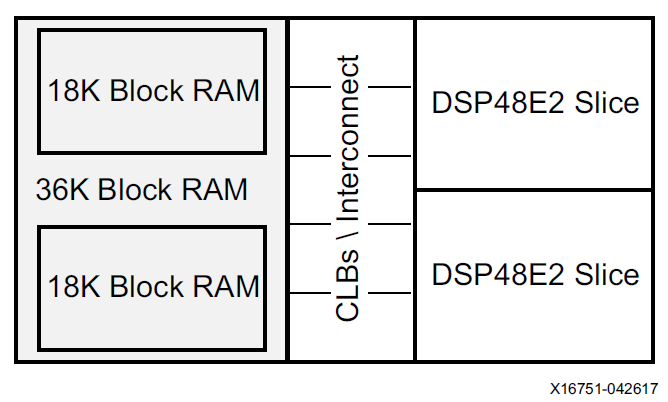
Zynq器件中通常将2个DSP48E2和一个36Kb的block memory以及5个CLB放置在一起,一个36Kb的BRAM可以拆分成2个18Kb的memory使用,每个memory可以独自被一个DSP占用。这样的配置也为DSP以及存储的高效配合使用提供了模板。后边我们可以利用这样的结构构建一个conv计算单元。同时多个DSP在FPGA芯片内部是垂直摆放的,这有利于多个DSP的cascade。
现在来看一下如何使用DSP阵列来构建低功耗的加法树。在传统的FIR滤波器中,乘累加的普遍做法是将多个乘法的输出通过多级加法器累加起来,需要的加法器级数是计算数据量的log2函数。比如一个如下滤波器:
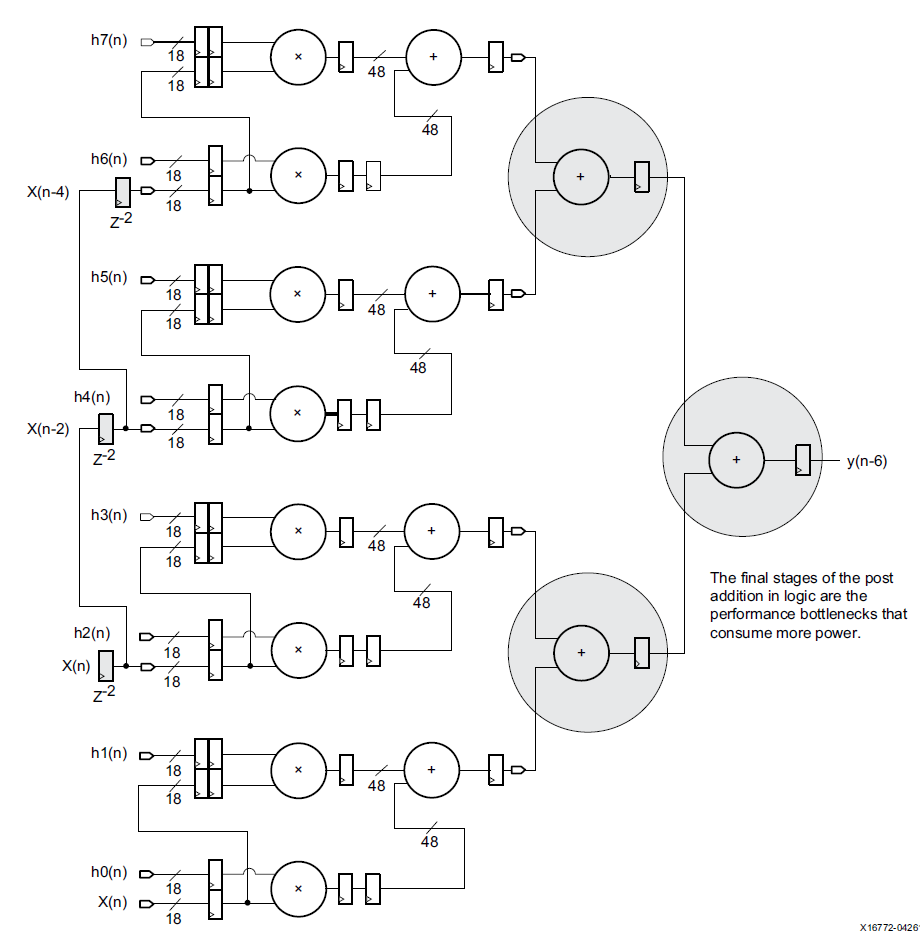
使用加法树会采用这样的结构:
这样的加法树会消耗更多的资源,代价以及能耗。特别是后几级的加法器位宽变的越来越宽,对LUT资源消耗很多。如果我们利用DSP的级联功能,可以完全实现FIR中的多输入加法功能。DSP中提供的post-adder以及CARRYCASCIN和CARRYCASCOUT可以选择上一级DSP的输出,同时将本级输出作为下一级输入。但是要注意级联的长度收到post-adder加法器位宽的限制,对于48bit的post-addr,如果乘法的输出长度为32bit,那么其级联长度可以达到2^16。
2 conv实现
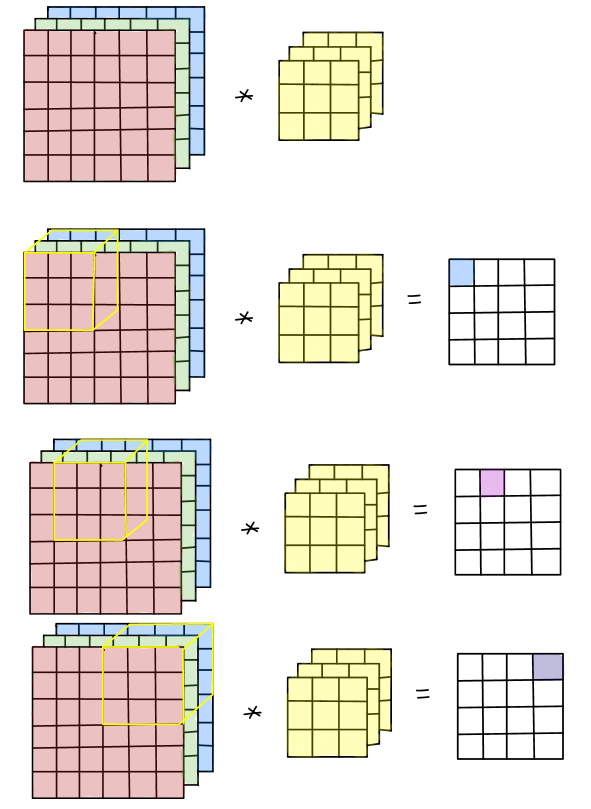
CNN中一个卷积层的feature map有三个维度:长(H),宽(W),输入通道(I)。输出的feature map也同样有三个维度长(H),宽(W),输出通道(O)。卷积核的维度就是4个维度:对应着feature map的H,W以及I和O。一个输出通道O的feature map是每个输入通道feature map的卷积结果的和。
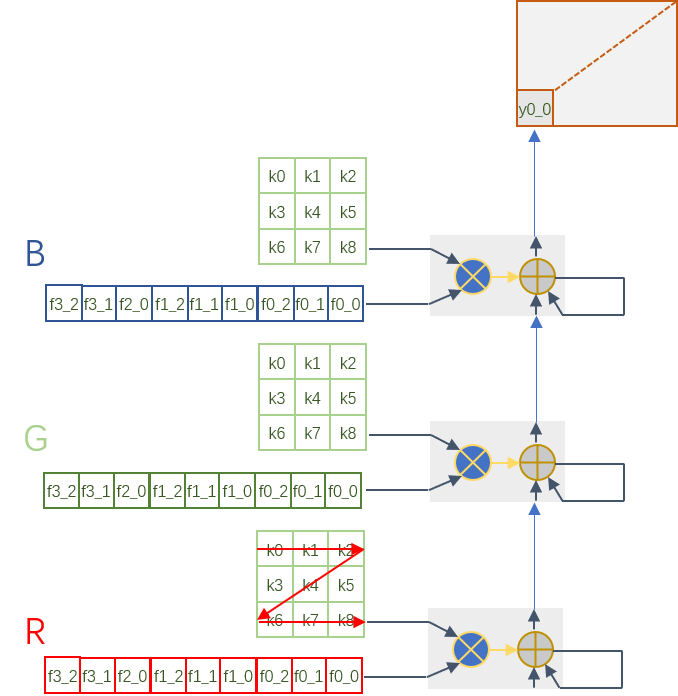
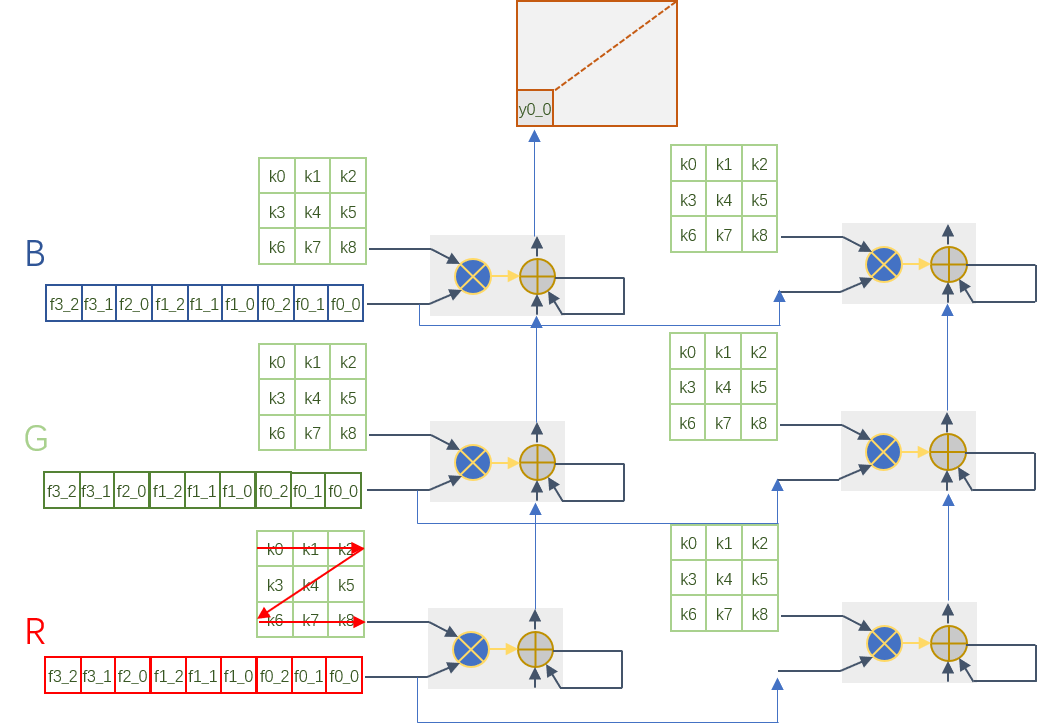
依据这样的运算特点,我们首先利用DSP的垂直结构和cascade特性构建一列运算单元,这个计算链包括DSP,BRAM以及一些LUT逻辑,每个DSP的输出作为下一级DSP的输入。DSP的端口A和D分别用于kernel和feature map数据的输入,kernel参数存储在BRAM中,36Kb BRAM作为2个18Kb BRAM使用,这样每个DSP都独自占用一个存储单元。我们以3x3卷积为例(stride为1,3输入通道),DSP阵列以及计算结构如下图所示:
每个BRAM中存储9个核参数,按照先H后W的方向读取送入DSP,feature map相对应的按照3x3卷积计算方向读取,先读取一个窗的数据,计算出一个元素结果,然后滑窗读取下一个窗的数据。每个DSP输出和下一次DSP的结果进行累加得到一个窗卷积的结果,然后这个结果再传递到下一个DSP用于feature map不同通道之间的求和。这里面有几个方面要考虑到:第一个是从一个DSP传递到下一个DSP有时间延迟,所以下一个DSP再进行通道之间数据求和的时候要有延时,这个可以通过延时读取kernel和feature map来处理。同时需要有使能信号控制DSP输出用于自身累加还是送入下一个DSP计算。当每个36Kb BRAM被拆分为2个18Kb BRAM的时候,18Kb BRAM读写公用相同口,所以将kernel写入bram的时候和从BRAM读数不能够冲突,当然这个可以通过使用ping pong buffer来解决。
我们现在通过一列的DSP可以实现一个输出通道的卷积计算了,如果我们沿着横向增加DSP列数,就可以实现多输出通道的卷积计算了。Feature map每个输出通道是共享的,因此数据可以沿着横向广播到其它列来进行计算。
3 乘法器复用
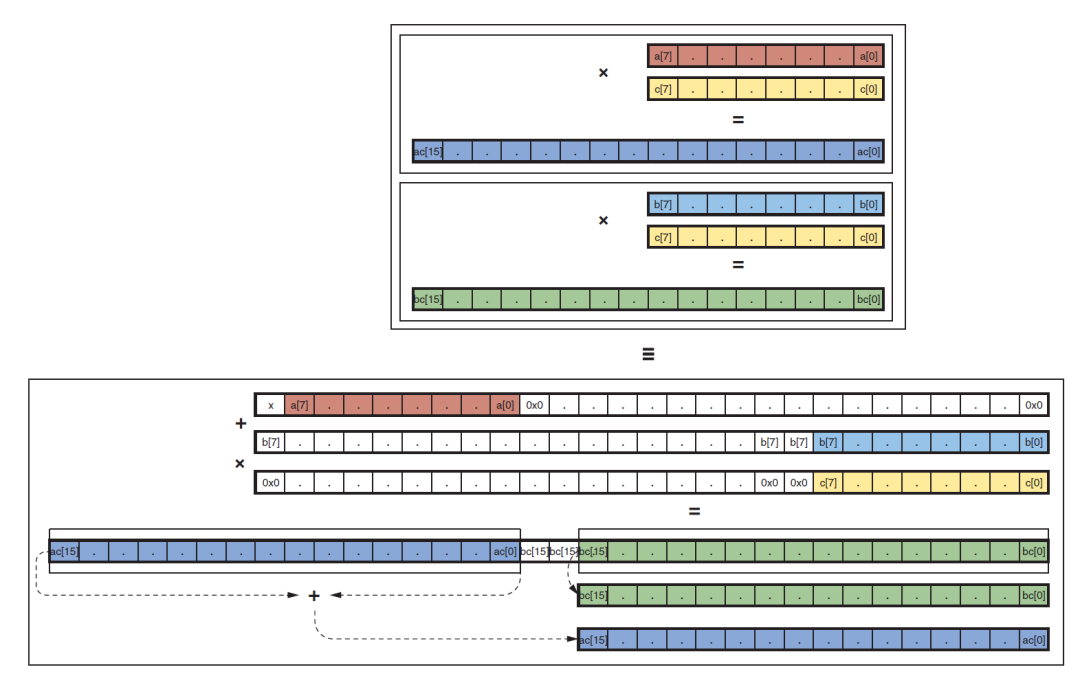
INT16,INT8和INT4是神经网络经常量化的数据类型。DSP48E2的乘法器是27x18的,因此INT16xINT16的只能同时计算一次。但是对INT8和INT4可以利用DSP的前加器实现乘法计算次数的翻倍。
我们发现两个INT8乘法结果位宽是16bit,因此我们可以利用pre-adder将两个INT8数据打包在一起。使得multiplier的27bit端口包含两个INT8数据。如下公式表达了计算过程:
因为bc数据位宽为16bit,所以ac和bc的数据区分开了。我们从结果中取出低16bit作为bc的结果,而ac的结果受到了bc符号位的影响,其值相当于减了一个符号位数值,所以要获得ac的结果需要取出偏移18bit结果加上符号位数值才是最终结果。如果符号位为1,则+1,如果符号位为0,则直接提取出来就可以了。
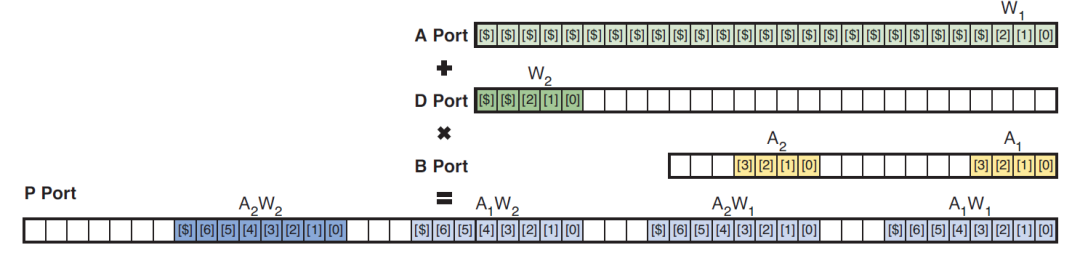
运用同样的思路,我们能够实现4路INT4的乘法,方法如下:
1) 利用pre-adder打包两个INT4数据,然后再利用B端口拼接两个正数数据。这种实现可以针对任何符号数据的乘法,因为pre-adder打包的数据可以有符号,所以我们可以通过转换将B端口数据的符号位转换到pre-adder端口上来。
2) 需要对打包的数据进行偏移,偏移保证4个结果不会发生混叠。可以进行如下偏移:
这样低8bit就是A1*W1的结果,然后依次取出其它结果,同时加上符号位。
通过以上的处理,可以最大化利用DSP的计算能力,实现1个INT16,2个INT8和4个INT4的乘法。DSP的频率通常都高于外部逻辑和BRAM的频率(DSP最高频率是BRAM频率的2倍),所以可以让DSP工作于高频,而外部逻辑工作于低频,这样能够让DSP的计算再有所提升。BRAM以2倍的数据位宽供数,而DSP以倍频方式工作,实现计算的增倍。那么相对于低频工作时钟来说,DSP就可以实现2倍INT16,INT8,INT4的乘法了。
对Intel的DSP没有使用过,这里就根据其官方文档进行一些浅显的了解吧。相比于DSP48E2,Intel的DSP计算功能更为强大,可以同时支持可变精度的顶点计算以及单精度浮点计算,浮点计算在DSP48E2中是不支持的。其定点计算功能包括:
1) 支持18bit和27bit的位宽。
2) 能够实现两个18x19和一个27x27的乘法运算。
3) 内部有加法器和减法器,能够实现两个乘法结果的求和,还有64bit累加器实现历史结果累加。
4) 有cascade级联,用于多DSP block串联,这已经是DSP普遍的拓展功能。
5) 内部含有寄存器组用于储存参数,特别适用于filter操作。
6) 支持rounding。
浮点计算功能包括:
1) 支持通常的浮点乘法,加法,减法,乘加和乘减等。
2) 支持同级联累加结果的乘法。
3) 支持复数乘法。
4) 支持一些异常报错。
5) 支持vector的点乘操作。
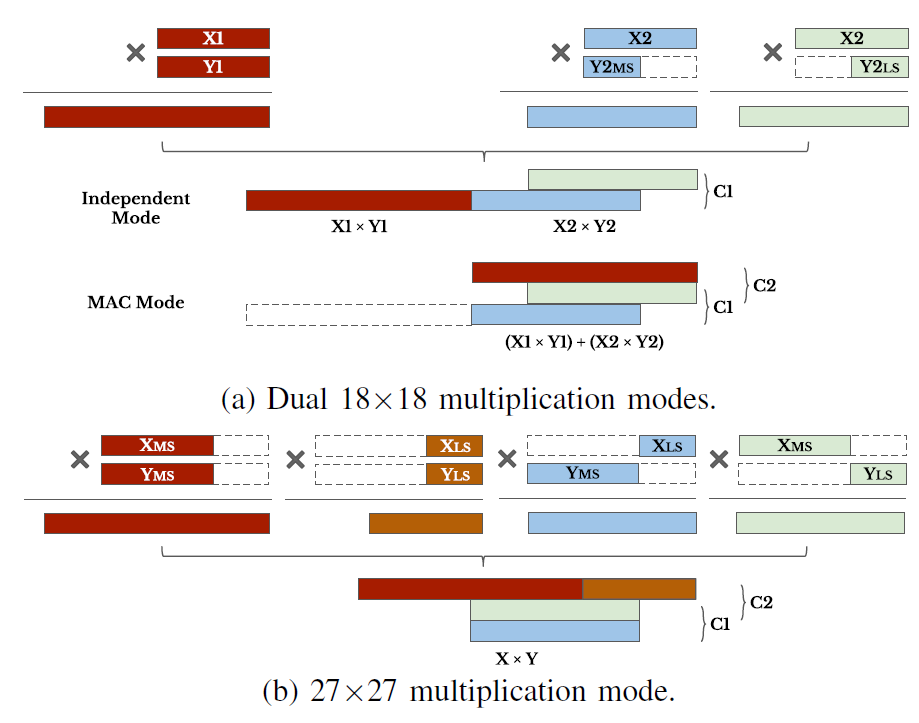
在双18x19乘法模式下,结够如下图:
前加器能够选择性实现加法或者减法,也可以通过internal coeficient模块控制input和内部参数的选择,内部参数能够支持8个不同的常数参数。双18x19的乘法结果可以通过post-adder实现求和,也可以将结果独立输出。利用这种模式能够实现复数计算,仅仅需要两个DSP就可以实现,如图:
在双乘法模式下,可以支持2个INT16乘法,2个INT8和4个INT4乘法。而在27x27模式下可以支持1个INT16,2个INT8和4个INT4的乘法。
在浮点模式下,DSP可以支持浮点数乘法,加减法以及MAC。同时还支持浮点数计算报错,有助于计算中的debug。在乘法模式下,支持的异常有:mult_invalid(浮点乘法操作过程异常,导致结果不正确,这个时候结果会是NaN),mult_inexact(结果是rounded的,超过极大值或者极小值),mult_underflow(结果下溢),mult_overflow(结果发生上溢)。加法模式下支持的异常也有类似情形:adder_overflow, adder_underflow, adder_inexact, adder_invalid。而MAC模式下支持乘法和加法的所有异常检测。
前边梳理了Xilinx和Intel DSP硬核的功能和用法,但是我们还不知道DSP其内部的核心模块乘法器是如何设计的。加法器我们知道有很多设计方法:串行加法器,并行加法器,相对逻辑和算法都很简单。乘法器的设计相对就复杂了,接下来来研究一下。
乘法器
1 Baugh-Wooley算法
Baugh-Wooley是很古老很经典的一个乘法器算法,最早追溯到1973年,由Charles R.Baugh和Broce A.Wooley提出。1973年的时候大规模集成电路已经发展起来了,Intel已经造了第一个微处理器4004。中国当年集成电路产业刚刚起步,那个时候才开始自己研制的第一块PMOS电路,同年引入外国单台设备并开始建设自己的工艺线。这个时候距离FPGA出现还有10年的时间。
乘数和被乘数使用二进制补码表示如下:
其中an和bn是符号表示,1表示负数,0表示正数。ai和bi是A和B中实际数值的表示。A*B在二进制补码表示下结果为:
从上边方程看出,结果中有加法也有减法,这是不统一的,不适合硬件的设计。Baugh-Wooley算法的核心就在于对减法的转换,抓换为加法就可以使用加法器来实现部分结果的求和了。如果将后两项的减法作为数据的负数符号位,用二进制补码表示,就能够转换为和前两项一样的加法,如下:
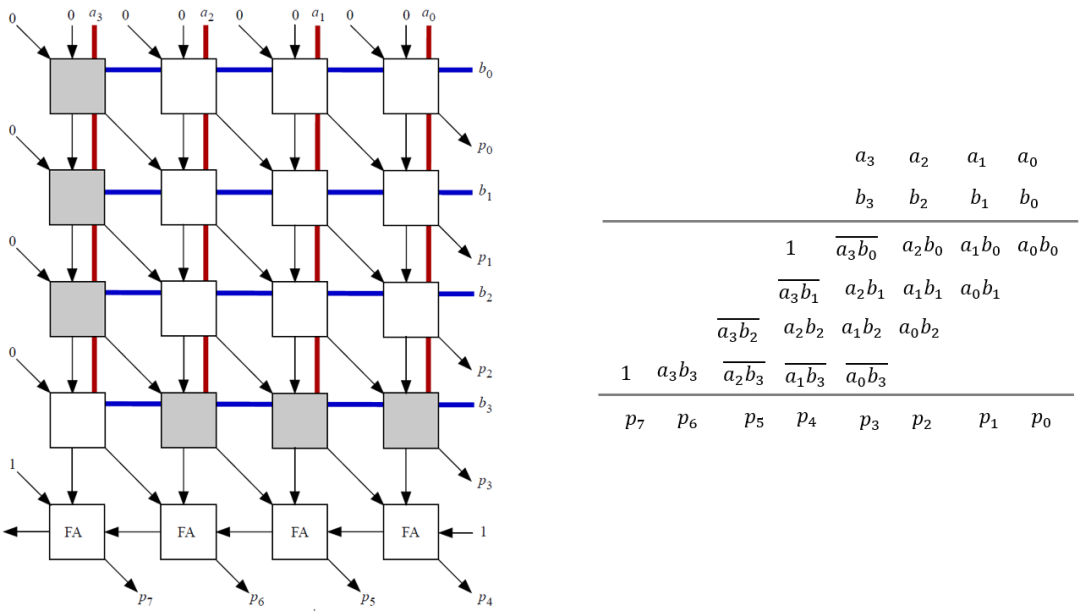
这样我们就可以设计出基本的4:2 compressor来作为乘法器的基本单元,这个compressor如下:
灰色单元是用于处理减法项的,这样我们就能够用一个二维阵列来构建一个乘法器了,比如对于4x4乘法有:
对于部分和边界需要对数据取反,同时还需要附加上上式的最后两项,对应着两个“1”。对于一个nxn的乘法来说,部分和有n个,所以最长级联链为n。这种乘法器随着数据宽度的增加级联线性增长,这会影响其延时。
2 基于Baugh-Wooley算法的可变位宽DSP设计
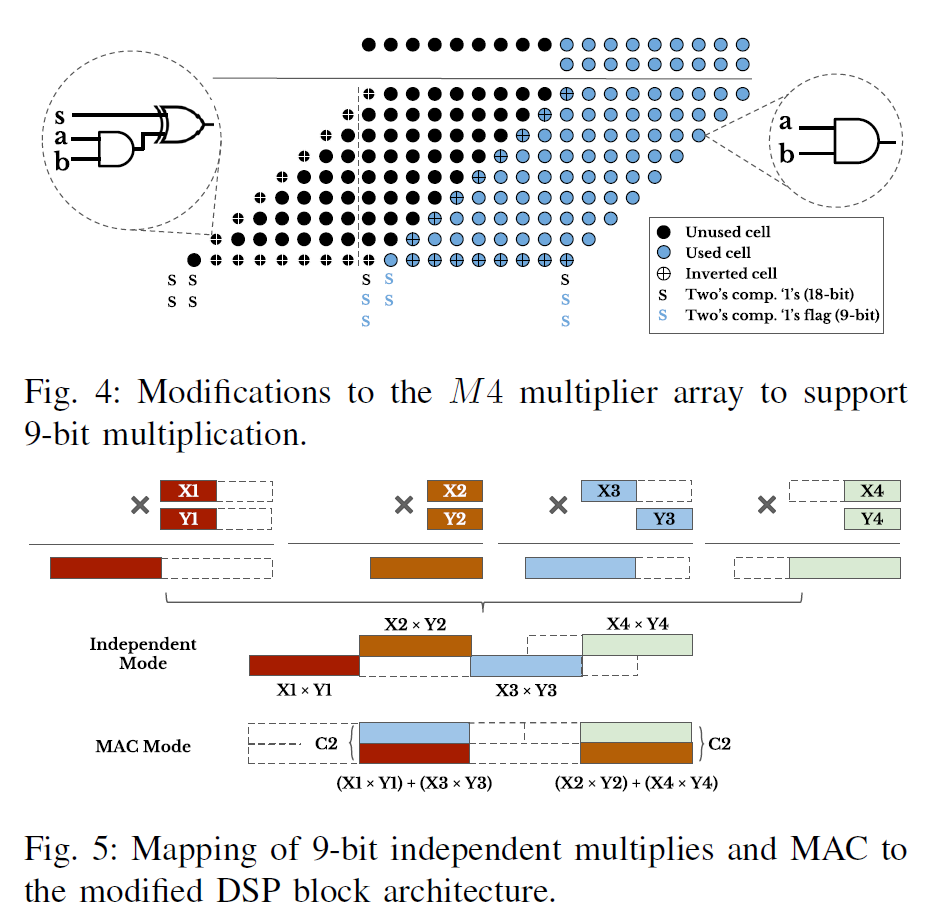
降低深度学习推理阶段的精度表示不仅仅可以改善加速器性能,而且可以降低模型存储以及DDR带宽需求。对于量化精度更宽的深度学习模型来说,FPGA的可编程性提供了更为灵活的bit宽度适配,这相比于其它硬件平台有更大优势。但是目前Xilinx和Intel中嵌入式硬核DSP的bit位宽固定(只支持18bit以下数据乘法),不能够有效的利用DSP资源来打包低bit数据乘法。于是有人从这一点出发来设计可变位宽乘法的DSP结构。本篇就介绍一篇基于Baugh-Wooley算法的改进的DSP结构。我们重点关注其实现27x27,18x18,9x9以及4x4乘法的方式和结构。
1 DSP基础版。
基础版结构类似于Arria-10器件中的DSP结构,其可以支持双18x18以及单路27x27乘法和累加(见下图)。它包含4个乘法器M1(18x18),M2(9x9),M3(9x18),M4(9x18)。乘法器M1以及M4输出有shift模块,这块可以用于实现乘法结果的分离。同时还添加了基于4:2compressor的加法器,可以支持多种计算模式(比如不同路乘法的求和等)。在双路18x18模式下,M1可以执行一个18x18的乘法计算,另外一个18x18的计算需要M3和M4乘法器进行配合,Y(其中一个乘数)可以被拆分为两部分(各9bit)用M3和M4执行乘法,然后在C1处完成求和。如果两路乘法结果要求和,可以通过C2实现,如果要输出两路结果,那么可以bypass C2。在27x27模式下,四个乘法器都被用到,依然采用类似的办法“分而治之”,将数据拆分为18bit和9bit,利用组合和移位实现。这里就不细说了。
2 DSP加强版。
对于比18bit更低的乘法计算,基础版本只能将数据拓展为18bit来进行计算,这样不能够有效利用DSP资源。这对于功率消耗很高的DSP来说存在巨大的功耗浪费,代价巨大。为了支持低bit乘法,需要对基础版进行改进。改进有以下几个挑战:
1) 改进版也必须兼容27x27和双18x18模式。
2) 保证输入输出接口不会增加,避免模块面积增大以及布线压力。
3) 改进版工作时钟不能低于600MHz(这是28nm器件DSP的普遍频率)。
先看9x9bit计算支持,根据72bit的输出端口,最大可以支持4个9x9计算(每个9x9输出18bit位宽,所以最高是4个乘法)。M1的输入最高位可以放有效的9bit数据,可以执行一个9x9乘法,M2也可以执行一个9x9乘法,因为M1有效结果向左偏移了18bit,不会和M2的重合,所以这样就实现了两个9x9乘法。关键在于M3和M4,其是18x9的乘法器,M3使用高9bit,M4使用低9bit,两个乘法结果还是会存在数据交叠。一种办法就是该进M4乘法器,使得其可以支持9x9乘法。改进的办法就是修改乘法器中基本Baugh-Wooley计算单元。需要将9x9乘法部分和的边界的cell修改为灰色(见Baugh-Wooley算法介绍)的cell。为了还能够兼容18x9的乘法,就需要有一个配置开关,来控制边界cell的模式。这回增加一些逻辑。
对于4x4的乘法,作者增加了4给4x4乘法器,同时修改M2和M3乘法器,使得其可以支持两路的4bit乘法,这根据Baugh-Wooley的结构去修改是可行的。我们可以选择去将一些无效的结果屏蔽掉来满足这种要求。这加强版DSP就可以执行8个4x4乘法了。虽然M1和M4是空闲的,同时增加了4个4x4乘法器,但是能够以最小的面积和逻辑代价换来计算性能的以倍提升也是值得的(可以看几种模式的芯片面积和逻辑)。
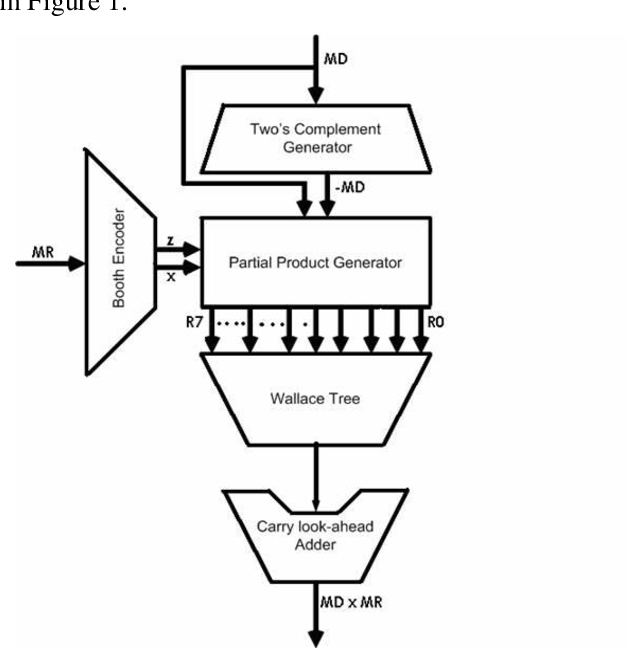
3 Booth算法
Baugh-Wooley算法中部分和进位链较长(等于乘数的位宽),这会限制乘法器的大小。A.D.Booth通过一种巧妙的办法可以减少部分和结果,大大降低了部分和求和的链路长度。其基本思想是对乘数(multiplier)重新编码,而被乘数(multiplicant)不变,以此降低乘数的位数。比如radix-2模式下,每2bit数据会被encode为0,1,-1三种数据类型,经过encode,乘数中连续为1的部分就会被0替代,而其它部分则不变,经过这样就大大降低了部分和数目。具体过程如下:
1) 在乘数最后一位添加0,然后观察乘数位数是否为2的倍数,如果不是最高位扩充符号位;
2) 从右至左依次遍历每两个bit位;
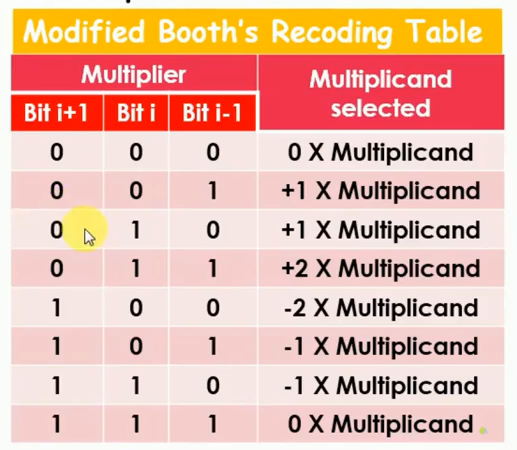
3) 进行如下encoder:00,11 -> 0,01 -> 1, 10 -> -1。
4) 然后使用encode的乘数和被乘数进行乘法计算。0和被乘数结果为0,这样就节省了一个部分和,因此对于连续111的数据,就可以节省了部分和的计算。1和被乘数y结果y,-1和y结果为-y,-y可以转变为二进制补码形式,这样就将减法转化为加法。之后使用加法树将这些结果加起来就可以了。
用的最多的是radix-4算法,其将连续的3bit数据encode为0,1,-1,-2,2表示。因为2的乘法只需要将数据左移一位就可以实现了,所以实现起来简单。而-2是结果移位后取补码结果,也容易实现。因此radix-4算法用途很广。Booth算法减少了加法进位链,能够实现更快速的乘法运算。
4 基于Booth算法的可变位宽DSP设计
选择radix-4作为乘法器基本单元有一个巨大的优势是:在保持乘法计算简洁的同时,将部分和数目降低了一半。一个基本的Booth乘法器结构如下:
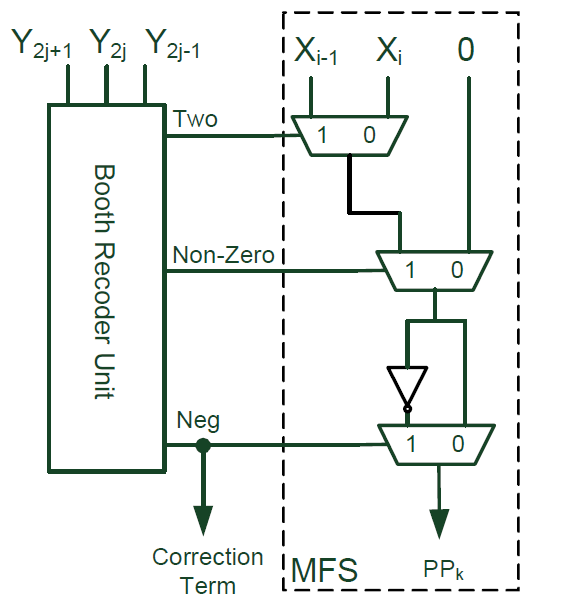
Booth encode的具体操作是:将最低bit后边补0,然后每三个数据遍历,按照表格encode为(0,1,-1,-2,2)中的数据,然后向左移动2bit,再进行3bit数据encode。然后计算encode后的multiplier和multiplicant的乘法。
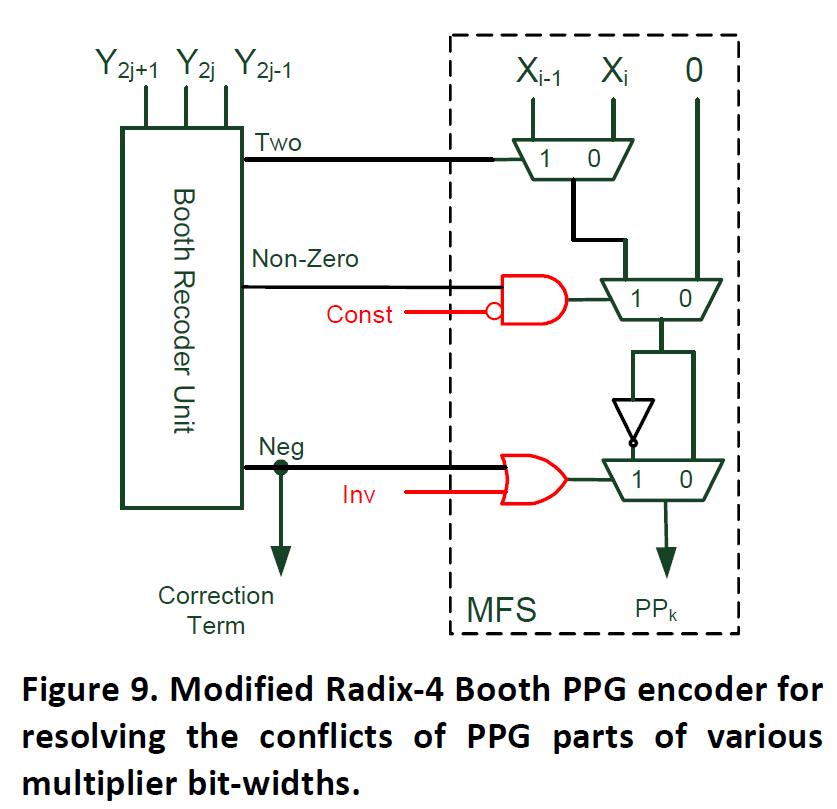
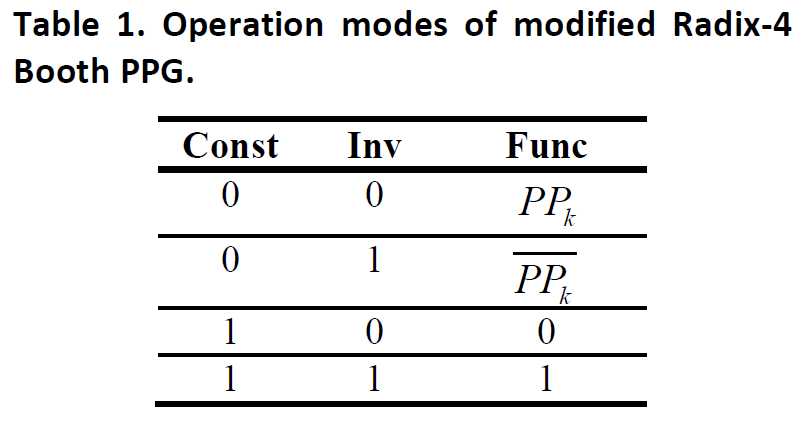
看看作者如何通过对部分和生成模块(PPG)的一个简单修改来实现可变数据位宽乘法的。PPG的基本结构如下图所示:
其中当encode值为负数的时候,符号位需要参与到部分和求和(PPR)中,作者将这个correction term传递到PPR中进行计算。由于Booth算法需要对每一个bit乘数进行encode,因此当位宽发生改变了的时候,就需要在符号位和encoded位进行选择,这样对于不同乘数位宽的配置来说,就需要很多multiplexer。一个简单有效的办法是先清除部分结果中的符号位扩展。我们可以给符号扩展位加1,加1之后符号扩展位就变成了一个inverted数。这样部分和中的符号位就可以用0和一个inverted的符号位替代。而在部分和求和后面在通过-1来实现。所有部分和扩展位-1可以综合起来用一个常数替代。
而通过对PPG模块的一个简单修改就可以达到这个目的,就是增加两个信号:
这样我们就可以实现高效可变位宽乘法器。
审核编辑:刘清
 电子发烧友App
电子发烧友App






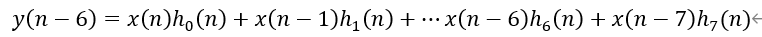
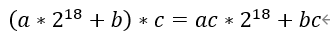
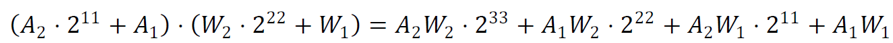
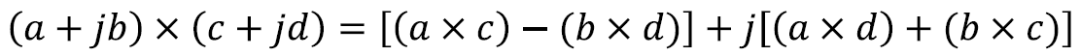
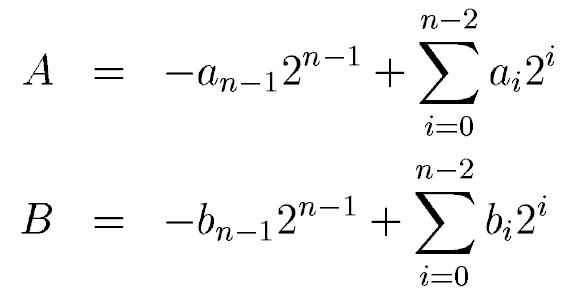
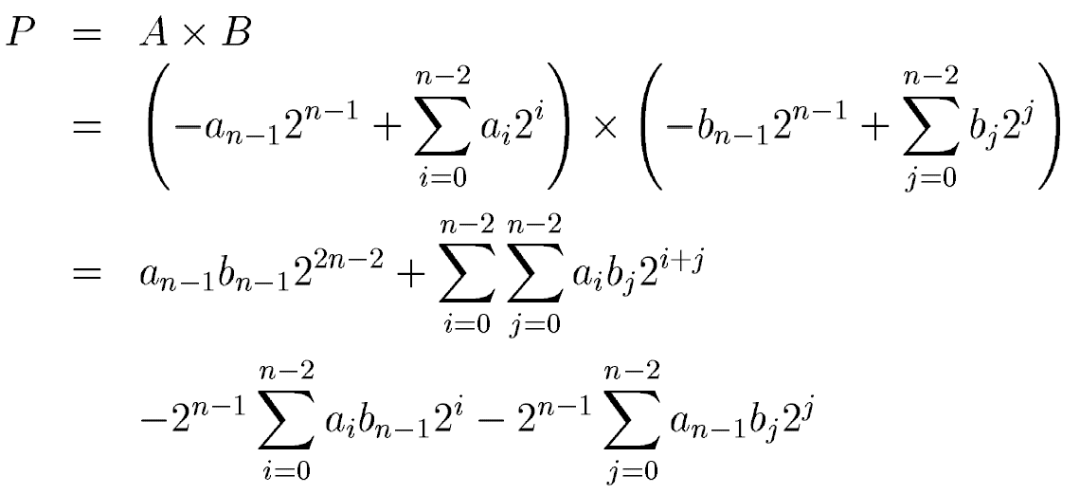
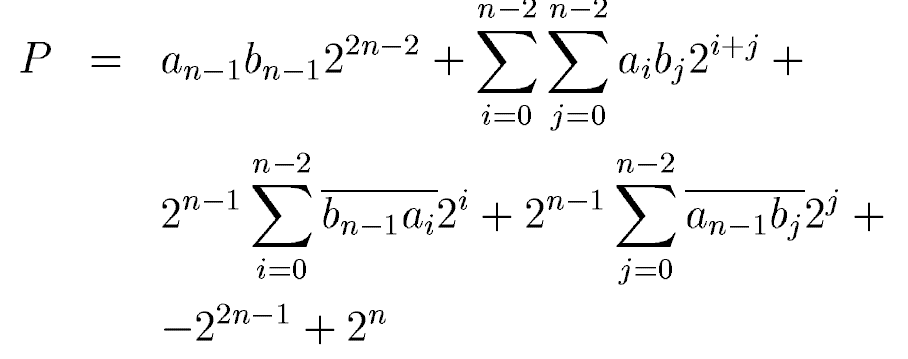

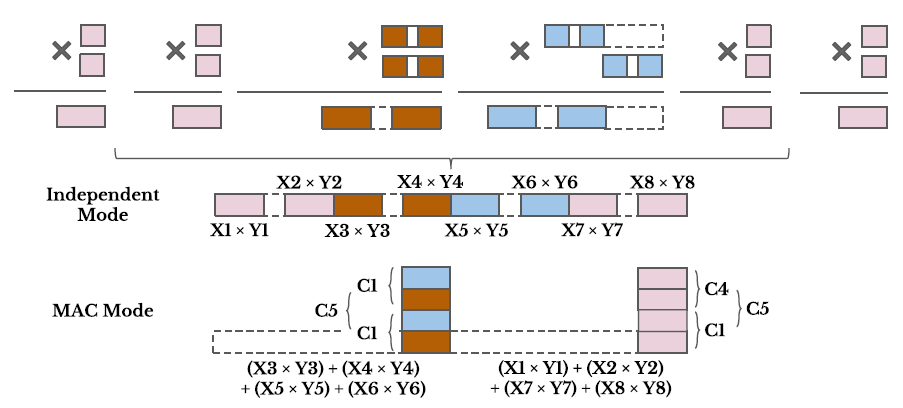
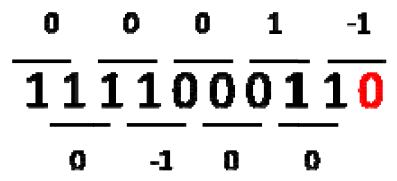





















评论