摘 要:本文研究了一种运用FPGA进行数据处理的方法,包括:提取输入数据的高log2M个比特位的数据,作为高有效位,根据预先设置的目标函数的计算表格,查找所述高有效位对应的目标函数值y(n)以及高有效位+1对应的目标函数值y(n+1);提取输入数据的剩余比特位数据,作为低有效位,并将所述低有效位与y(n)和y(n+1)的差值相乘,得到偏移值off(n),将该偏移值与所述高有效位对应的目标函数值y(n)相加,将计算结果作为所述输入数据对应的目标函数值。本方法具有控制简单、结构规则、单运算周期、计算精度较高的特点,适合于FPGA的数据处理实现。
引言
现场可编程门阵列(FPGA)芯片在许多领域均有广泛的应用,尤其是在无线通信领域。FPGA具有极强的实时性和并行处理能力,这使其对信号进行实时处理成为可能。FPGA内部一般都包含逻辑单元(查找表/触发器)、存储单元(BRAM)、乘加单元(MAC)和一些其他的时钟、引脚单元等[1-3]。
现代数字信号处理的主要发展趋势是:算法结构日趋复杂,计算量大,实时性要求高,并且包含大量的三角函数、开方、对数等复杂函数的计算。但FPGA内部的乘加单元并不适合直接进行此类函数的计算,需要把各种复杂函数分解为简单的移位、加法和乘法结构,进而在FPGA中实现[4]。
当前,在FPGA上实现三角函数、开方、对数等复杂函数的计算,技术领域最常见的是除法,其次为开方和三角函数,很少涉及对数和其他复杂一些的函数。而在FPGA具体的实现上,此类函数一般采用直接查表法或幂级数展开法,对于三角函数和开方的计算,也会采用CORDIC的计算方法,但这三种方法的应用都有一定的局限性[4]。
1 现有的FPGA实现方法
(1)在FPGA上采用直接查表方法,来实现函数的计算,具有:
优点——通用性强、结构简单;
缺点——随着输入位宽的增加,内部存储量的消耗呈指数性增长。
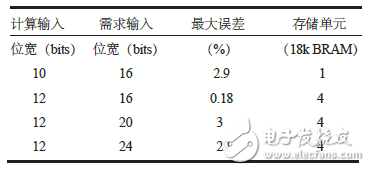
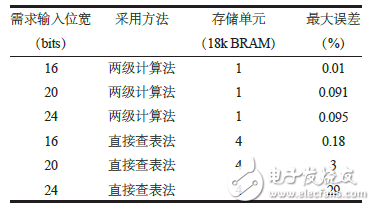
表1给出了不同输入输出位宽所需要的存储单元(BRAM)。
表1 不同输入输出位宽所需要的存储单元
可以看出,输入输出位宽较小时,直接查表法可以满足实现要求,但在数字信号处理领域,输入输出一般都在16bits以上,这时采用直接查表法就很难满足实现需求。
这里以开方算法为例进行说明。采用直接查表法进行开方计算有2种方式。
方式一:在完全保证精度的条件下,采用直接查表法。若开方为16bits输入16bits输出,在完全保证精度的条件下,FPGA就需要存储216深度的数据,需要64块18k BRAM的存储空间。而一片中等FPGA一般包含几十块到几百块的18k BRAM存储单元,此时计算就要用掉大部分的存储单元,显然不满足实现的资源需求。
方式二:降低精度,减少输入位宽,采用直接查表法。
表2 直接查表法开方误差表
可以看出,随着实际有效输入的增加,计算精度变大,很难满足计算的误差要求。
(2)在FPGA上采用幂级数展开法计算函数。
优点——计算精度可控,多级展开可以达到较高的计算精度;
缺点——幂级数展开法为了达到较高的精度,需要多级展开,这样就需要采用较多的资源来实现。
以exp为例(0~π/4范围内),采用三角函数幂级数展开法:
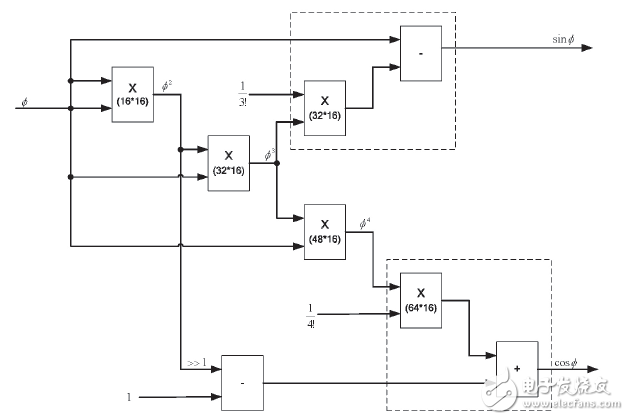
若输入为16bits,采用幂级数展开法的计算框图如图1。
从资源方面考虑,三角函数幂级数展开法在FPGA中的实现需要5级乘法和3级加法,考虑每级乘法位宽需要扩展,实际需要FPGA的12个乘法器
(18bits×18bits)资源。此外从误差方面考虑,0~π/4范围内,cosΦ的最大误差为0.046%, sinΦ的最大误差为0.35%。
图 1 幂级数展开法实现exp计算
此外幂级数展开法的应用范围也比较有限,开方、倒数、对数、三角函数的计算可以采用幂级数展开法,但对于等较复杂的函数计算就不再适合用此方法进行计算。
(3)在FPGA上采用CORDIC法来实现函数的计算。
优点:将复杂的运算分解为简单移位、加迭代
运算,结构规则,运算周期可以预测,比较适合于FPGA实现;
缺点:一般使用多周期方式,单周期方式资源消耗较高,并且计算仅限于向量旋转、开方等有限的范围。
采用CORCIC计算三角函数,16bits输入,在多周期条件下需要500个左右的LUT/FFs,在单周期条件下,需要1000个左右的LUT/FFs。
2 本文提出的方法
本文在FPGA上采用两级方法进行函数计算:第一级,直接利用输入数据的高有效位确定计算结果的有效范围;第二级,直接利用输入数据的低有效位进行计算结果的误差调整。本研究方法充分利用FPGA内部的各种逻辑资源、乘加器(或乘法器)资源和BRAM资源:可以根据FPGA内部BRAM资源的大小采用相应深度的数据表存储第一级数据的有效范围;采用FPGA内部的乘加器(或乘法器)资源进行乘加操作。此方法具有控制简单,结构规则,单运算周期,计算精度较高的特点,适合于FPGA的算法实现。
此外,采用本研究方法的两级计算的方法,不同函数的计算实现方法一致,只要修改第一级计算高有效位数据表格中的数据,就可以复用设计,有利于资源共享和模块化实现。
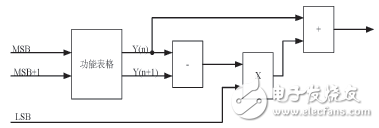
图2 FPGA两级法进行函数的计算
同现有方案的比较分析:
(1)同直接查表法比较
以开方为例进行,资源和误差的列表如表3。可以看出,在资源和误差方面,本研究方法在FPGA上实现函数计算优势明显。此外,FPGA可以通过增加存储单元和扩展输出位宽来进一步提高计算精度。
表3 两级计算法开方同直接查表法误差比较表
(2)同幂级数展开法的比较
首先,本问题出的新方法比幂级数展开法的应用范围更广泛。其次,在同样的函数下,以exp的计算为例,本文提出的新方法资源更好,误差更小。在资源方面,FPGA上采用的两级计算方法, 同时计算只需要2个乘法器即可,远远少于幂级数展开法的资源消耗;在误差方面,0~π/4范围内,16bits输入,cosΦ和sinΦ的最大误差都小于10-5,因此此方法误差比幂级数展开法误差要小。
(3)同CORDIC方法比较
首先,本文提出的新方法比幂级数展开法的应用范围更广泛。其次,在同样的函数下,以exp的计算为例,新方法资源消耗相对较少,cosΦ和sinΦ同时计算只需要300个左右的LUT/FFs即可。而且,新方法采用的是单运算周期模式,运算速度更高。
3 实现流程
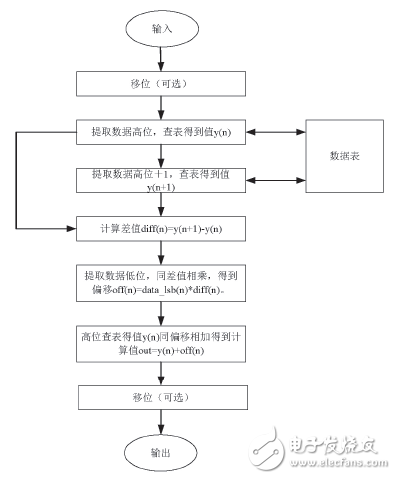
如图3所示,本论文采取的实现方法如下:
步骤一:根据一维函数的计算,预先生成一定深度的计算表格;
步骤二:移位(可选),把数据的高有效位移位成1,增加较小数据的计算精度;
步骤三:提取数据的高bits,作为第一级数据表的地址,得到数据值y(n);
步骤四:提取数据的高bits,加1后作为第一级数据表的地址,得到下一个数据值y(n+1);
步骤五:计算差值diff(n)=y(n+1)-y(n);
步骤六:提取数据的低bits,作为有效的偏移数据,同计算的差值相乘,得到偏移off(n)=data_lsb(n)*diff(n);
步骤七:高位查表数据值y(n)同偏移相加得到计算值out=y(n)+off(n);
步骤八:根据步骤一的移位逆操作(可选),得到实际输出值。
图3 FPGA两级法求解函数的流程框图
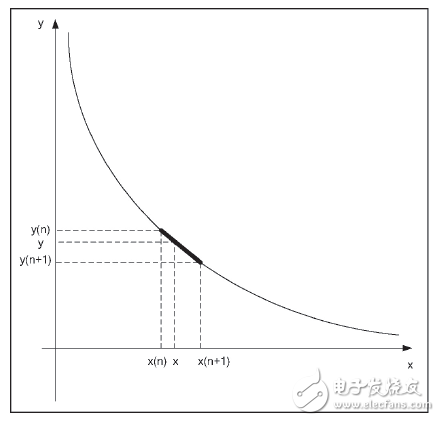
如图4所示,对本研究方法进行进一步的详细说明。
对于任意一个一维函数,若采样点足够密集,那么任何2个采样点之间可以看作是线性关系,可以通过插值的方法来计算。
图4 FPGA两级法求解函数的详细说明
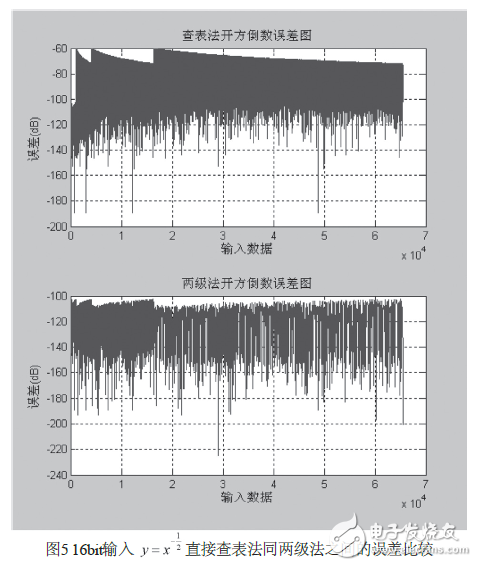
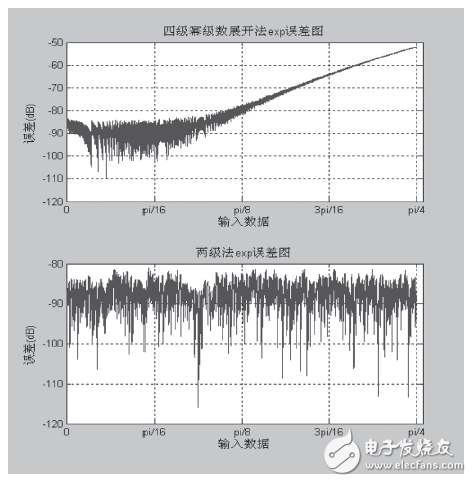
由图6可得出,两极法的误差范围更小。
4 结论
在现代数字信号处理方面,FPGA具有极强的实时性和并行处理能力[5]。在FPGA的实现上,本文介绍了现有的直接查表法、幂级数展开法、CORDIC计算方法的优缺点。在此基础上,本文研究了基于FPGA的两极计算法,并把它和以上三种方法进行比较,得出两极算法具有控制简单、结构规则、单运算周期、计算精度较高的特点。此外,本文详细介绍了两极算法的实现流程,并举例来进行说明,使读者能够更好地掌握两极算法。
参考文献
Xilinx-Virtex7 Data Sheets. 2014.11.
Xilinx-Virtex7 User Guides. 2014.11.
Altera-Stratix V Device Datasheet. 2015.7.
贝耶尔.数字信号处理的FPGA实现(第3版)[M].2011.
John G.Proakis,Dimitris G.Manolakis.数字信号处理――原理、算法与应用(第四版)[M].
 电子发烧友App
电子发烧友App







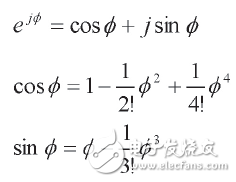



















评论