锁相环在通信、雷达、测量和自动化控制等领域应用极为广泛,已经成为各种电子设备中必不可少的基本部件。随着电子技术向数字化方向发展,需要采用数字方式实现信号的锁相处理。因此,对全数字锁相环的研究和应用得到了越来越多的关注。
传统的数字锁相环系统是希望通过采用具有低通特性的环路滤波器,获得稳定的振荡控制数据。对于高阶全数字锁相环,其数字滤波器常常采用基于DSP 的运算电路。这种结构的锁相环,当环路带宽很窄时,环路滤波器的实现将需要很大的电路量,这给专用集成电路的应用和片上系统SOC(system on chip)的设计带来一定困难。另一种类型的全数字锁相环是采用脉冲序列低通滤波计数电路作为环路滤波器,如随机徘徊序列滤波器、先N 后M 序列滤波器等。这些电路通过对鉴相模块产生的相位误差脉冲进行计数运算,获得可控振荡器模块的振荡控制参数。由于脉冲序列低通滤波计数方法是一个比较复杂的非线性处理过程,难以进行线性近似,因此,无法采用系统传递函数的分析方法确定锁相环的设计参数。不能实现对高阶数字锁相环性能指标的解藕控制和分析,无法满足较高的应用需求。
本文提出了一种基于比例积分(PI)控制算法的高阶全数字锁相环。给出了该锁相系统的具体结构,建立了系统数学模型,并对其系统性能进行了理论分析。采用MATLAB 软件对系统进行了仿真实验。应用EDA 技术设计了该锁相系统。
2 全数字锁相环的结构及工作原理
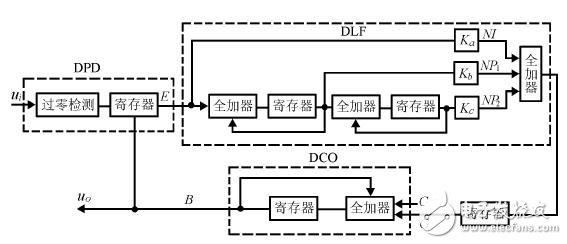
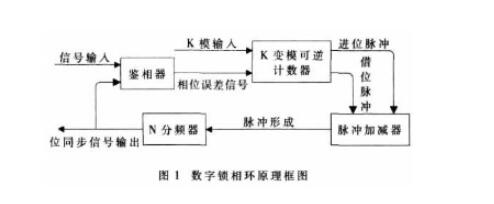
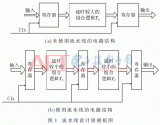
基于比例积分控制算法的三阶全数字锁相环的系统结构如图1 所示。该系统由数字鉴相器(DPD)、数字环路滤波器(DLF)和数控振荡器(DCO)三个部件组成。 图1 三阶全数字锁相环系统结构图
本锁相系统中由于数控振荡器采用累加器的结构,因此,累加器输出的并行码就是数控振荡器的输出相位码B,它反映了输入信号和输出信号之间的瞬时相位差。鉴相器中的寄存器是由一组D 触发器构成。DCO 的输出相位码B 并行送到D 触发器的D 端,在输入信号的正向过零点对D 触发器采样,D 触发器组的输出E 就表示该采样时刻的瞬时相位差,从而完成了数字鉴相功能。
数字环路滤波器的主要作用是抑制噪声及高频分量,并且控制着环路相位校正的速度与精度。为了提高锁相系统的性能,设计了基于PI 控制算法的二阶数字滤波器。其工作原理是对鉴相器输出的相位误差信号经一阶积分环节、二阶积分环节和比例环节调节后,分别产生积分控制参数NP1 和NP2,以及比例控制参数NI,然后取这三个控制参数之和作为数控振荡器的控制参数。为使DLF 输出的控制码组在同一瞬间并行送入DCO,在这两个环路部件之间接入一缓冲寄存器。
数控振荡器是由全加器和寄存器构成的累加器组成。若累加器位长为N,则低位输入端NL 接DLF的控制码组G,高位NH 接DCO 自由振荡频率0 f 的控制码组C(该参数可由设计者设定)。当控制码组G 均为‘0’时,DCO 输出端最高位AN 的输出信号的频率便是DCO 的自由振荡频率f0 。在环路锁定过程中,控制码组G 不是全为零,此时累加器的累加结果将进位而改变累加器的分频系数,从而改变DCO 输出信号的频率,实现比例积分控制参数对本地估算信号的控制作用,最终达到锁相的目的。
3 数字锁相环系统性能的理论分析
3.1 锁相环的系统结构
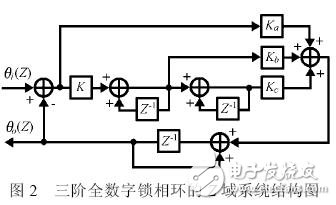
若采样周期很短,并且把数字鉴相器、数字环路滤波器和数控振荡器的增益系数归并到环路总增益一起考虑,可画出锁相环在Z 域的系统结构如图2 所示。
图2 中θi(Z)为锁相环的输入信号;θo(Z) 为锁相环的输出信号; K 为环路总增益; Ka 为比例环节系数; Kb 为一阶积分环节系数; Kc 为二阶积分环节系数。
由图2 可以分别写出该锁相环开环、闭环和误差Z 域传递函数:
3.2 锁相环系统的稳态分析
3.2.1 系统的稳定性
由离散系统的奈奎斯特判据可知,环路系统稳定的充分必要条件是闭环传递函数的特征根必须全部位于Z 平面的单位圆内,只要有一个在单位圆外,系统就不稳定。由式(2)可得环路的特征方程为:
利用朱例(Jury)稳定判据,可以根据系统闭环特性方程的系数来判别特征根是否位于Z 平面的单位圆内,从而判别系统是否稳定。经分析推导可得,该三阶数字锁相环系统稳定的所有条件为:
3.2.2 系统跟踪误差
由系统误差传递函数可以计算环路在各种不同输入信号作用下的稳态跟踪误差,即:
θi(Z) 为输入信号, He(Z) 为锁相系统误差传递函数。由式(6)所求得的本系统对应于各种典型相位输入信号的稳态跟踪误差列于表1。
由表1 可知,本锁相系统对于相位阶跃、频率阶跃和频率斜升输入信号的稳态跟踪误差为零。
4 锁相系统的设计实现与仿真
依据图1 锁相环系统的结构,利用Xilinx 公司的ISE 设计软件,采用自顶向下的模块化设计方法,用VHDL 对全数字锁相环的各个部件分别进行编程设计,然后对该系统做综合设计和仿真。最后,采用Xilinx 公司的sparnⅡ系列的FPGA 器件实现了锁相系统的硬件功能。
本锁相系统的设计参数如下:鉴相器中D 触发器的位长为16;DLF 内二个积分环节中累加器的位长均为16;DCO 中累加器的位长为24,累加器的时钟频率fclk 为8MHz,比例积分控制码组的字长G=14,自由振荡频率 f0 控制码组的字长C=10。
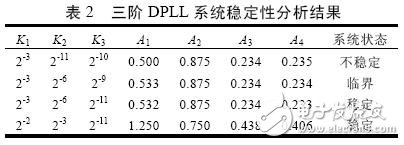
选择不同的比例系数Ka 和积分系数Kb 、Kc ,可以改变K1 、K2 、K3 的参数值,进而可根据本锁相系统的稳定条件式(5),判断系统是否稳定。表2 列出了几种典型参数所对应的锁相系统稳定性分析结果。
表2 中设
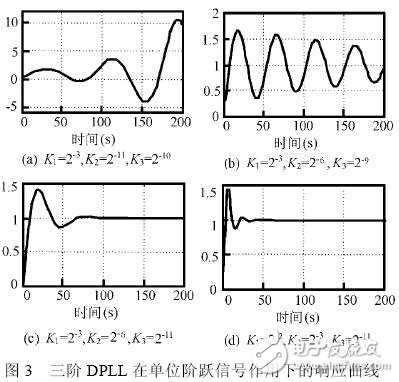
根据本系统在Z 域的传递函数和表2 中的设计参数K1 、K2 、K3 ,应用MATLAB 软件进行分析,得到三阶全数字锁相环在单位阶跃信号作用下的系统仿真曲线如图3 所示。
从图3 中系统仿真曲线可以看出,仿真实验与理论分析的结果是一致的。调节比例和积分系数不仅能够控制锁相系统的稳定性,还可以控制系统的锁相速度。显然,在保持系统稳定的条件下,图3(d)设计参数所对应的系统锁相速度较快。
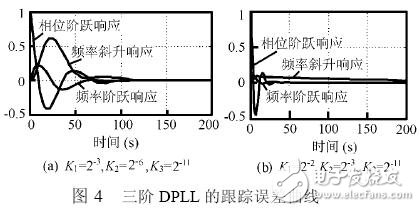
根据本系统在Z 域的误差传递函数和实际设计参数,可以分别得到系统在相位阶跃、频率阶跃和频率斜升信号作用下的响应曲线如图4 所示。从图4 中可以看到,系统对于上述信号的稳态跟踪误差均为零。这与理论分析所得出的结论也是一致的。综合考虑锁相系统的稳定性、稳态相差和锁相速度等性能指标, 最终选择设计参数K1 = 2-3 , K2 = 2-6, K3 = 2-11。
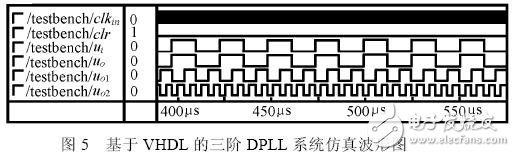
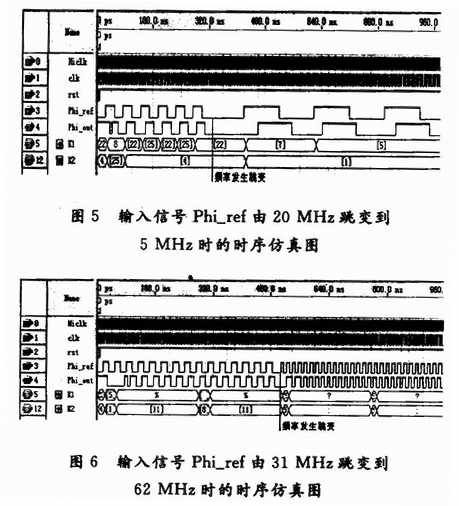
图5 给出了采用EDA 技术设计的三阶全数字锁相环的系统仿真波形,图中clkin 为系统时钟信号,clr 为系统复位信号, ui 为输入信号, uo 为输出信号, uo1 为二倍频输出信号, uo2 为四倍频输出信号。从图5 中可见,本锁相系统可以同时得到倍频输出信号。
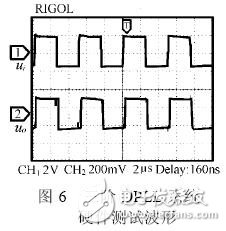
图6 给出了用FPGA 实现的三阶全数字锁相环的硬件电路测试波形。系统仿真与硬件测试结果都表明,该系统能够实现锁相功能。
4 结论
本文提出了一种基于PI 控制算法的三阶全数字锁相环,采用EDA 技术进行系统设计,并用可编程逻辑器件予以实现。该锁相环具有电路结构简单、控制灵活、跟踪精度高、环路性能好、易于集成的特点。在锁相速度和稳定性方面优于已有的采用脉冲序列低通滤波计数方法实现的数字锁相系统。理论分析和仿真实验表明,改变比例积分控制参数,可以很方便地调节锁相系统的锁相速度和稳定性,因而简化了设计过程。硬件测试结果证实,应用EDA 技术设计的高阶全数字锁相环够实现其锁相功能。该锁相环可作为功能模块嵌入SoC 内,为各种控制系统提供快速、稳定和高精度的同步信号。
参考文献:
[1] Dr Best Roland E. Phase-Locked loops: Theory, Dsign and Applications [M]. New York:Mcgraw-Hill, 1984.
[2] 王福昌, 鲁昆生. 锁相技术 [M]. 武汉: 华中科技大学, 2002.
[3] 潘松, 黄继业, 王国栋. 现代DSP 技术 [M]. 西安: 西安电子科技大学出版社, 2003.
[4] Lindsey William C, Chie Chak Ming. A survey of digital phase-locked loops [J]. Proceedings of the IEEE, 1981, 69(4): 410-431.
[5] Walters Stephen M, Troudet Terry. Digital phase-locked loop with jitter bounded [J]. IEEE Transactions on Circuits and Systems, 1989,36(7): 980-986.
[6] 胡华春, 石玉. 数字锁相环原理与应用 [M]. 上海: 上海科学技术出版社, 1990.
[7] 庞浩, 俎云霄, 王赞基. 一种新型的全数字锁相环 [J]. 中国电机工程学报, 2003(2): 37-41.
[8] 孟宪元. 可编程ASIC 设计及应用 [M]. 成都: 电子科技大学出版社, 2000.
[9] 薛定宇, 陈阳泉. 系统仿真技术与应用 [M]. 北京: 清华大学出版社, 2004.
 电子发烧友App
电子发烧友App







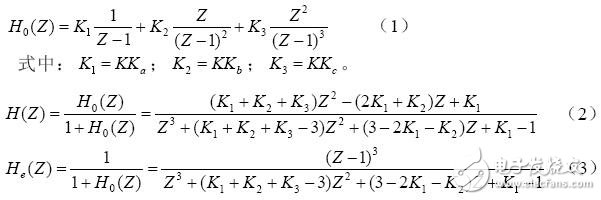















评论