视距法测距基本原理

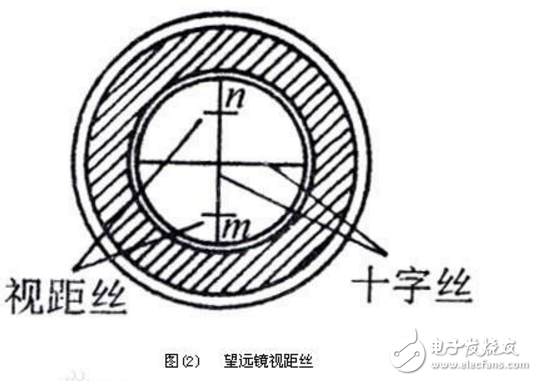
　　视距测量是利用经纬仪、水准仪的望远镜内十字丝分划板上的视距丝在视距尺（水准尺）上读数，根据光学和几何学原理，同时测定仪器到地面点的水平距离和高差的一种方法。

　　视距测量具有操作简便、速度快、不受地面起伏变化的影响的优点，被广泛应用于碎部测量中。但其测距精度低，约为：1/200-1/300。

　　测量原理

　　拇指测距（三角函数与密位） 向前伸直手臂树起拇指，闭上左眼，右眼、拇指、目标形成直线，闭上右眼，睁开左眼，此时记住左眼、拇指延长直线目标右侧那一点，目测那一点与目标的距离并乘以10，即你到目标的大概距离。

　　“大拇指测距法”是根据直角三角函数来测量的假设距离我们N米有一目标物，测量我们到目标物的距离：

　　1、水平端起我们的右手臂，右手握拳并立起大拇指

　　2、用右眼（左眼闭）将大拇指的左边与目标物重叠在一条直线上；

　　3、右手臂和大拇指不动，闭上右眼，再用左眼观测大拇指左边，会发现这个边线离开目标物右边一段距离；

　　4、估算这段距离（这个也可以测量），将这个距离×10，得数就是我们距离目标物的约略距离。

　　由于每个人的臂长、两眼瞳孔间距各有不同，因此，这种测距法需要因人而异，进行严格训练，经过普通训练的一般人可以做到200米内正负误差5米。

　　视距测量是利用望远镜内的视距装置配合视距尺根据几何光学和三角测量原理，同时测定距离和高差的方法。

　　特点：这种方法具有操作方便，速度快，不受地面高低起伏限制等优点

　　水平视距

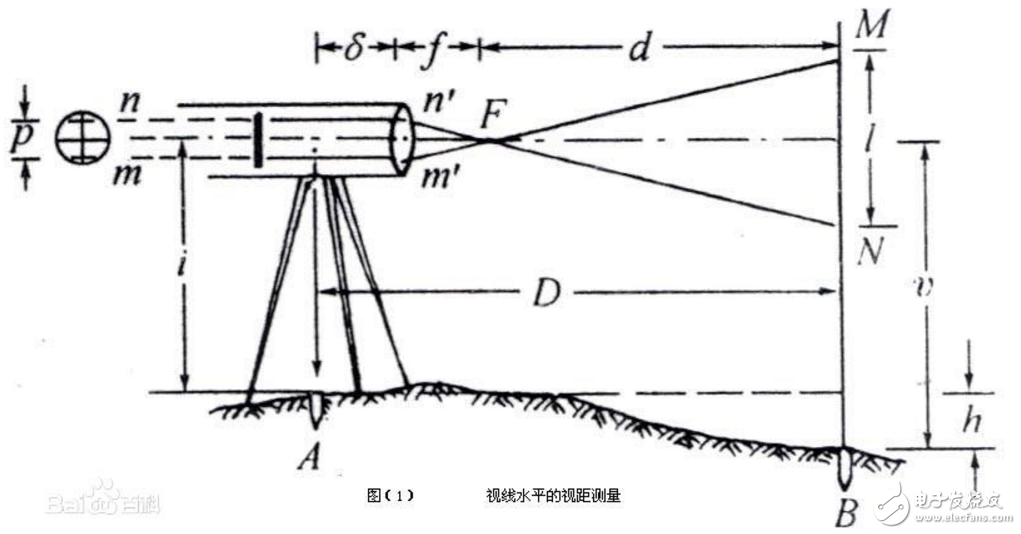
　　如图（1）所示，欲测定A，B两点间的水平距离D及高差h，可在A点安置经纬仪，B点立视距尺，设望远镜视线水平，瞄准B点视距尺，此时视线与视距尺垂直。若尺上M，N点成像在十字丝分划板上的两根视距丝m，n处，那末尺上MN的长度可由上，下视距丝读数之差求得。上，下丝读数之差称为视距间隔或尺间隔。

　　图（1）中l为视距间隔，p为上、下视距丝的间距，f为物镜焦距，δ为物镜至仪器中心的距离。

　　

　　由相似三角形m‘n’F与MNF可得：d：f=l：p ，即：d=fl /p，由图看出D=d+f+δ ，带入得：D=fl/p+f+δ，令f/p=K，f+δ=C，得D=Kl+C.（1）

　　式中K、C——视距乘常数和视距加常数。现代常用的内对光望远镜的视距常数，设计时已使K=100，C接近于零。则公式（1）可化简为D=Kl=100×l。（2）

　　而高差h=i-v， （3）

　　i—仪器高，是桩顶到仪器横轴中心的高度；v—瞄准高，是十字丝中丝在尺上的读数。

　

　　倾斜视距

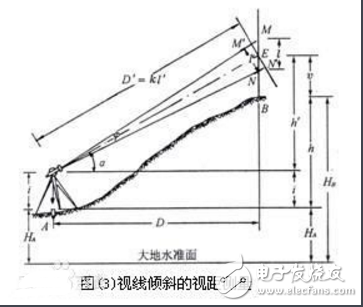
　　在地面起伏较大的地区进行视距测量时，必须使视线倾斜才能读取视距间隔，如图（3）。由于视线不垂直于视距尺，故不能直接应用上述公式。如果能将视距间隔MN换算为与视线垂直的视距间隔M‘N’，这样就可按公式（2）计算视距，也就是图（3）斜距D’，再根据D‘和竖直角α算出水平距离D及高差h。因此解决这个问题的关键在于求出MN与与M’N‘之间的关系。

　　图中φ角很小，约为34‘，故可把角MM’E和角NN‘E 近似地视为直角，容易计算得l’=M’N‘=MNcosα=lcosα，则D’=Klcosα。（4）

　　容易求得水平距离D=Klcosα*cosα，（5）

　　高差h=D*tanα+i-v 。 （6）

　　其实视线水平的时候α为0°，sin0°=0，cos0°=1，带入（4）、（5）、（6）就可得到（2）、（3）式。其中视线水平的时候视距等于水平距离。

　　

　　观测计算

　　施测时，如图（3）所示，安置仪器于A点，量出仪器高i，转动照准部瞄准B点视距尺，分别读取上、下、中三丝的读数M、N、V，计算视距间隔l=M-N。再使竖盘指标水准管气泡居中（如为竖盘指标自动补偿装置的经纬仪则无此项操作），读取竖盘读数，并计算竖直角α。然后按公式（4）、（5）、（6）用计算器计算出视距、水平距离和高差。