基于深度相机的机器人视觉系统设计

葛绍强，杨永辉，周自维

（辽宁科技大学 电子信息与工程学院，辽宁 鞍山 114051）

摘  要：针对工业机器人视觉领域中现有手眼标定方法复杂的问题，提出一种基于3D视觉的简便手眼标定方法即将3D深度相机和矿山爆破机器人相结合，利用3D深度相机能够获取空间点坐标的原理以及3个参考点的几何关系，获取标定板上参考点到相机的坐标转换关系。同时机器人末端法兰盘中心到机器人基坐标系的转换关系已知，可利用 TSAI 两步法求取相机到机器人末端法兰盘中心的转换关系，继而求得参考点在机器人基坐标系中的位姿。把此手眼标定方法应用到矿山爆破机器人系统中，实验结果表明，最大坐标误差为 5.7 mm，最小误差为 0 mm，精度满足现场矿山孔洞的定位要求。该文的创新点是利用深度相机的原理和 3个点的几何关系求取参考点到相机的转换关系。

中图分类号：TN876⁃34；TP242；TP391.41   文献标识码：A

文章编号：1004⁃373X（2022）02⁃0172⁃05

0 引 言

目前，视觉工业机器人在工业生产中有很多应用，比如机器人抓取、焊接、喷涂、搬运等各个方面[1]。在工业机器人视觉领域中，手眼标定的主要目的是获取相机到机器人末端法兰盘的转换关系[2⁃3]，根据这种转换关系将空间中点的坐标转换到机器人基坐标系下，这样才能更好地控制机器人的手臂去完成相应的任务，因此手眼标定的研究对于工业机器人视觉有着重大的意义。对于手眼标定的研究，文献[4]中叙述了手眼标定的定义；文献[5]提出一种相机标定和四点位姿估计的手眼标定方法，但该方法需要进行相机标定获取相机的外参，即需要获取标定板到相机的转换关系；文献[6]提出一种高精度的手眼标定方法，对标定过程中采集的图像进行校正，提高相机外参的精度，进而进行手眼标定。文献[7]提出一种基于ROS的机器人自动手眼标定方法，其中利用PnP的方法求解标定板到相机的转换关系。对于手眼标定复杂的问题，本文根据深度相机的原理和棋盘格上的参考点的几何关系，求取参考点到相机的转换关系，再结合机器人末端法兰盘到机器人基坐标系的转换关系，求解相机到机器人末端法兰盘的转换关系。

1 矿山爆破机器人视觉系统设计

矿山爆破机器人视觉系统,由六自由度工业机器人(KUKA R16⁃2F)、深度相机 RealsenseD435、机器人抓取工具组成，采用眼在手上的方式，将深度相机固定在机器人末端处，深度相机随着机器人的位姿变换而变化，这种类型的手眼标定，相机的视野更大。矿山爆破机器人视觉系统结构图如图1所示。

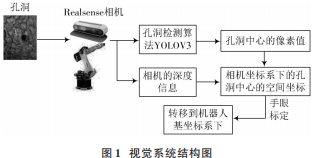
首先，相机利用深度学习算法YOLOV3识别出矿山中的孔洞，得出孔洞中心点的像素坐标；然后，结合深度相机原理计算出孔洞中心在相机坐标系下的空间坐标，随后结合手眼标定关系，将孔洞中心的空间坐标转换到机器人基坐标系下。  

2 手眼标定

2.1 手眼标定原理介绍

手眼标定分为两种类型：一种是眼在手上的手眼标定(Eye⁃in⁃Hand)；一种是眼在手外的手眼标定(Eye⁃to⁃Hand)[8]。本文主要叙述眼在手上的手眼标定类型，首先对照下手眼标定的示意图，如图2所示。Base表示机器人的基坐标系，在机器人末端法兰盘上安装一个相机（图中Center表示法兰盘的中心，Camera表示的是相机),在机器人视野前面固定一个标定板（棋盘格,图中用Checkerboard表示),棋盘格上的某个参考点与机器人基坐标的关系是固定不变的，利用这个不变的关系进行机器人的手眼标定。

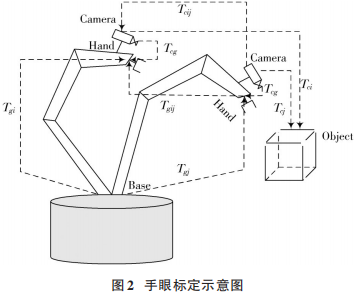
用示教器控制机器人移动，让相机拍摄棋盘格标定板，把此时的机器人位姿定义为1，用Tgi 表示机器人末端法兰中心到机器人基坐标系下的转换关系，Tcg表示相机坐标系到机器人末端法兰中心的转换关系（待求，这个关系是固定不变的),Tci表示参考点到相机的转换关系。同样控制机器人移动到另外一个位姿下，把此时的机器人位姿定义为 2，用 Tgj表示机器人末端法兰中心到机器人基坐标下的转换关系,Tcg仍然是相机坐标系到机器人法兰中心的转换关系，Tcj 表示此时参考点到相机的转换关系。Tgij表示位姿1 和位姿2机器人末端法兰中心坐标系之间的相对位置的齐次变换矩阵。Tcij表示位姿 1和位姿2下特征点到相机的转换关系的齐次变换矩阵[9]。根据标定板上棋盘格中的某参考点到机器人基坐标系下的转换关系不变的原则有如下关系：

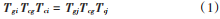
首先，对式（1）两边同时右乘T-1ci ，得：

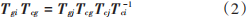
再对式（2）两边同时乘T-1gj ，得：

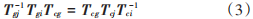
式中：T-1gj Tgi就是表示位姿1和位姿2之间的法兰中心坐标系的齐次变换矩阵Tgij；TcjT-1ci就是表示位姿1和位姿2下参考点到相机转换关系的齐次变换矩阵Tcij。得到：

可以令Tgij=A, Tcij=B, Tcg=X,得：

式中，A,B 已知，那么手眼标定的问题转换成求解AX=XB的问题[10⁃14]，求解X利用 TSAI两步法求解。

2.2 参考点姿态确定方法 根据参考点的像素值、深度值和深度相RealsenseD435的SDK函数rs2_deproject_pixel_to_point（），获取棋盘格上参考点的空间坐标，这里参考点选择3个，且这3个点构成一个直角三角形，利用直角三角形有两个边相互垂直的原理，可确定角度为90°的参考点姿态。具体原理如图3所示。

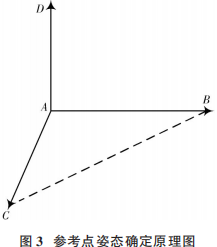
根据图3所示，A，B，C 三点构成一个直角三角形，AB和BC两边相互垂直，且A，B，C 三点在相机坐标系下的空间由3D相机原理获得，根据A，B两点的空间坐标和A，C 两点的空间坐标，可以计算出向量AB 和向量AC，让两个向量作叉积，即可得向量AD，向量AD与平面ABC垂直；接着让向量AD与向量AC作叉积运算，确保向量AB和平面ACD 垂直；然后分别对向量AB，向量AC，向量AB作单位化处理，该结果即是A点的姿态。棋盘格上的参考点A，B，C三点的示意图如图4所示。

已知A点处的姿态的空间坐标（位置）和姿态，就可确定A点的位姿，或者说是参考点到相机的转换关系矩阵。  

3 手眼标定实验与分析

根据第2节手眼标定的叙述，画出了整个手眼标定的流程图，如图5所示。根据图5所示，首先操作机器人到位姿1处，拍摄棋盘格图片，根据特征点的几何关系确定点的姿态，姿态和位置已知，计算参考点到相机的转换关系矩阵，同时计算机器人末端到机器人基坐标系的转换关系矩阵。反复操作机器人到9个不同的位姿处，可以获得 9张棋盘格图片、9组参考点到相机的转换关系和9组机器人末端到机器人基坐标系下的变换矩阵，8组Tgij和8组Tcij。9张图片如图6所示。

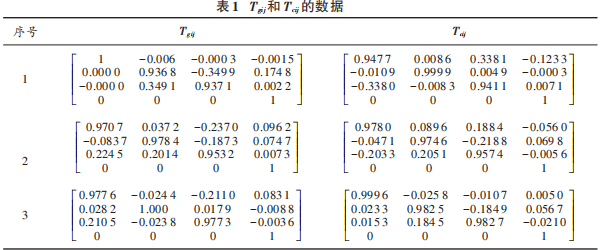
取8组Tgij和8组Tcij中的3组数据如表1所示。

根据8组Tgij和8组Tcij数据，再结合TSAI两步法，即可求得相机到机器人末端的转换关系矩阵Tcg ，用Matlab程序进行仿真，求Tcg 矩阵和在机器人基坐标系下，参考点与相机的相对位置的关系图，Tcg如下：

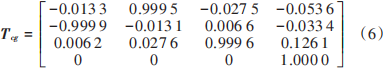
相对位置关系如图7所示。

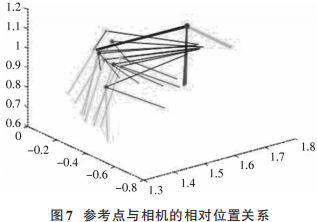
图7中，分散的点表示相机的姿态，密集的点表示参考点的姿态。

利用该标定关系，将棋盘格中参考点的像素坐标转换到机器人基坐标系下，参考点坐标在机器人基坐标系下的，理论值和实际值如表2所示。

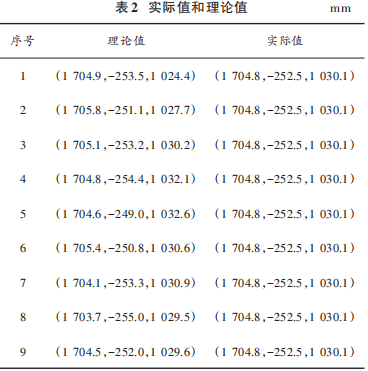
其中，理论值是根据Tgi*Tcg*Tci关系求得的，因为机器人共移动9个位姿，因此理论值有9个，实际值是根据控制机器人末端的法兰盘移动到参考点，根据示教器读出的该参考点在机器人基坐标系下的坐标且都为（1704.8，-252.5，1030.1）。从表中可以看出，其理论值中3个坐标值和实际值中3个坐标值的误差最大为5.7mm，最小误差为0mm。随后，搭建一个模拟矿井隧道，孔洞的半径大约控制在50 mm 左右，控制机器人工具抓取注药工具运动到炮孔中心测试，每次都能精准地抓取注药管运送到孔洞中心处，其精度满足矿山爆破的需求。测试过程中的实验图如图8所示。

4 结 语

本文提出一种基于深度相机的手眼标定方法，该标定平台利用棋盘格上的特征点几何关系，获取棋盘格上参考点到相机的转换关系矩阵，同时利用示教器读取的机器人末端的位姿计算机器人末端到机器人基坐标系下的转换矩阵，把这两个关系矩阵与TSAI两步法结合，即可求得相机到机器人末端法兰盘的转换关系。此过程充分利用深度相机的原理，不需要对其求取相机的外参，过程简便且精度满足矿山爆破任务的要求。该标定平台在其他应用工业机器人视觉领域中也有一定的借鉴意义。

注：本文通讯作者为杨永辉。

参 考 文 献

[1] 田鹏飞，杨树明，吴孜越，等 .结合精度补偿的机器人优化手眼标定方法[J].西安交通大学学报，2020（8）：99⁃106.

[2] 王昌云，李立君 . 基于四元数的机器人手眼标定算法[J]. 传感器与微系统，2019，38（12）：133⁃135.

[3] SHARIFZADEH S，BIRO I，KINNELL P. Robust hand ⁃ eyecalibration of 2D laser sensors using a single ⁃ plane calibrationartefact [J]. Robotics and computer ⁃ integrated manufacturing，2020，61：101823.

[4] WU L，WANG J L，QI L，et al. Simultaneous hand⁃eye，tool⁃flange，and robot ⁃ robot calibration for comanipulation bysolving the AXB=YCZ problem [J]. IEEE transactions onrobotics，2016，32（2）：413⁃428.

[5] 吴安成，何卫锋，欧阳祥波.基于OpenCV 的码垛机器人手眼标定方法[J].制造技术与机床，2018（6）：45⁃49.

[6] 任杰轩，张旭，刘少丽，等 . 一种高精度机器人手眼标定方法[J].现代制造工程，2020（4）：44⁃51.

[7] 陈宝存，吴巍，郭毓，等 .基于 ROS的机器人自动手眼标定系统设计[J].计算机仿真，2020，37（2）：343⁃348.

[8] 张妍 .工业机器人手眼标定精度分析研究[D].扬州：扬州大学，2019.

[9] 何佳唯，平雪良，刘洁，等 .一种机器人手眼关系混合标定方法[J].应用光学，2016，37（2）：250⁃255.

[10] LI H Y，MA Q L，WANG T M，et al. Simultaneous hand⁃eyeand robot ⁃world calibration by solving the AX = YB problemwithout correspondence [J]. IEEE robotics and automationletters，2015，1（1）：1.

[11] TABB A，YOUSEF K M A. Solving the robot⁃world hand⁃eye（s） calibration problem with iterative methods [J]. Machinevision and applications，2017，28（5/6）：569⁃590.

[12] MA Q， LI H， CHIRIKJIAN G S. New probabilisticapproaches to the AX=XB hand ⁃ eye calibration withoutcorrespondence [C]// 2016 IEEE International Conference onRobotics and Automation. Stockholm：IEEE，2016：4365 ⁃4371.

[13] GROSSMANN B，KRÜGER V. Continuous hand⁃eye calibrationusing 3D points [C]// 2017 IEEE 15th InternationalConference on Industrial Informatics. Germany：IEEE，2017：311⁃318.

[14] ZENG J，CAO G Z，LI W B，et al. An algorithm of hand⁃eyecalibration for arc welding robot [C]// 2019 16th InternationalConference on Ubiquitous Robots. Seoul：IEEE，2019：1⁃6.

作者简介：

葛绍强（1994—），男，安徽亳州人，硕士，主要研究方向为计算机视觉与机器人控制。

杨永辉（1971—），男，辽宁鞍山人，教授，主要研究方向为计算机视觉与智能控制。

周自维（1974—），男，辽宁鞍山人，副教授，主要研究方向为智能机器人与计算机视觉。

编辑：黄飞