一、常采用的几种坐标系
在鱼雷航行动力学的研究过程中,根据不同的研究目的,须要采用不同的坐标系。常采用的坐标系有以下几种:
1.地面坐标系
确定重心运动,应选择与地球固连的坐标系![]() 。此称为地面坐标系,如图2-1所示。 坐标原点
。此称为地面坐标系,如图2-1所示。 坐标原点![]() 选在地面适当的位置(例如鱼雷发射点或入水点)。
选在地面适当的位置(例如鱼雷发射点或入水点)。![]() 轴处于地平面内指向某一适当方向(例如指向鱼雷发射方向),此轴的方向称为参考航向;
轴处于地平面内指向某一适当方向(例如指向鱼雷发射方向),此轴的方向称为参考航向;![]() 轴垂直于地面并指向上方,此轴称为铅垂轴;
轴垂直于地面并指向上方,此轴称为铅垂轴;![]() 轴也处于地平面内,垂直于
轴也处于地平面内,垂直于![]() 平面。按右手坐标法则规定( 拇指代表
平面。按右手坐标法则规定( 拇指代表![]() 轴,食指代表
轴,食指代表![]() 轴,中指的 指向就是
轴,中指的 指向就是![]() 轴的方向 )。用地面坐标系描述鱼雷的弹道最方便。任一时刻的坐际(
轴的方向 )。用地面坐标系描述鱼雷的弹道最方便。任一时刻的坐际(![]() )确定了重心的瞬时位置,函数
)确定了重心的瞬时位置,函数![]() 描述了鱼雷重心的 空间运动的轨迹。
描述了鱼雷重心的 空间运动的轨迹。
2.雷体坐标系
描述雷体转动可选用与雷体固连的坐标系![]() ,此称为雷体坐标系,如图2-1所示。坐标原点O取在鱼雷重心处(假定鱼雷重心在雷体的对称轴上)。 三个坐标轴与雷体固连。
,此称为雷体坐标系,如图2-1所示。坐标原点O取在鱼雷重心处(假定鱼雷重心在雷体的对称轴上)。 三个坐标轴与雷体固连。![]() 轴处于雷体对称面内,与雷体几何对称轴一致,指向雷头,此轴称为雷体纵轴,
轴处于雷体对称面内,与雷体几何对称轴一致,指向雷头,此轴称为雷体纵轴,![]() 轴处于鱼雷纵对称面内, 垂直于
轴处于鱼雷纵对称面内, 垂直于![]() 轴,指向上方,此轴称为雷体立轴;
轴,指向上方,此轴称为雷体立轴;![]() 轴垂直于
轴垂直于![]() 平面, 从雷尾观察,
平面, 从雷尾观察,![]() 轴指向右方,此轴称为雷体横轴。
轴指向右方,此轴称为雷体横轴。
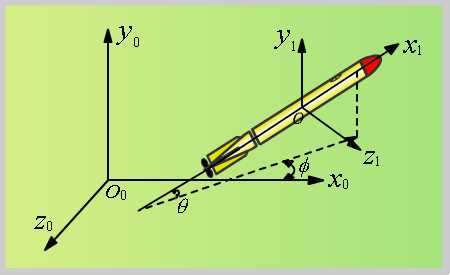
图2-1 地面坐标系与雷体坐标系
3.速度坐标系
为确定作用在雷体上的流体动力,须要描述鱼雷重心速度矢量v与雷体之间的相对位置, 可选用速度坐标系。OXYZ来表示(图2-2)。速度坐标系原点O也取在鱼雷重心处,OX轴与鱼雷重心轨迹的切线一致,其正方向为重心运动瞬时速度矢量v的方向,此轴称为速度轴。一般情况下,v不在鱼雷对称平面内。OY轴在雷体纵对称面内,且垂直于OX轴,指向上方,称为升力轴,OZ轴垂直于XOY平面,其方向按右手坐标法则确定,从雷尾观察指向右方,OZ的称为侧力轴。侧力轴一般不在雷体横鳍平面内。
 |
图2-2速度坐标系
4.平移坐标系
雷体坐标系相对于地面坐标系的旋转描述了鱼雷的旋转运动,但是,上述两坐标系的原点不一致,不便于研究其相对旋转。为此,再选择一种坐标系![]() ,使其坐标原点与鱼雷浮心重合,其
,使其坐标原点与鱼雷浮心重合,其![]() 各轴分别与地面坐标系的
各轴分别与地面坐标系的![]() 各轴对应平行。此坐标系是随浮心运动而平移的动坐标系,称为平移坐标系。
各轴对应平行。此坐标系是随浮心运动而平移的动坐标系,称为平移坐标系。
5.弹道坐标系(半速度坐标系)
由弹道定义可知,重心速度矢量V在空间的方向决定了弹道的切线方向。描述速度矢量V空间方向的两个角度参数称为弹道角,用弹道角来确定弹道问题更为方便。
为定义弹道角而选取弹道坐标系,如图2-3所示。坐标原点仍在重心上,OX轴仍为速度轴,但轴不在垂直鳍平面内,而是在包含速度矢量V的垂直平面之内,向上为正方向,轴按右手坐标法则确定。
图2-3 弹道坐标系
6.半雷体坐标系
如图2—4所示,半雷体坐标系的原点与雷体坐标系的原点重合;轴与OP重合,图中直线OP为速度轴OX在雷体系平面上的投影,轴与OY轴重合;轴与XOY平面垂直并指向鱼雷前进方向的右侧。由图2-2可以看出,当=0时,速度坐标系即与半雷体坐标系相重合。
在某些流体动力测试设备中,由于其天平结构的限制,只能在半雷体坐标系中测定流体动力参数。
图2-4 半雷体坐标系
二、鱼雷的运动状态参数
1.鱼雷的姿态角
雷体坐标系与地面坐标系之间的相对位置可用鱼雷的三个姿态角来表示。由于在描述旋转运动时,平移坐标系与地面坐标系完全等价,因此,鱼雷的旋转运动归结为雷体坐标系对平移坐标系的相对旋转。众所闻知,旋转运动可用一种欧拉角来描述。先令雷体坐标系与平移坐标系完全重合,然后使雷体坐标系按下列顺序绕其自身各轴旋转:先绕轴转动角度再绕旋转后的轴转动角度。最后绕二次旋转后的轴转动角度,这样就得到一组欧拉角.如图2-5所示。
(演示动画)
图2-5 鱼雷姿态角
欧拉角、和描述了鱼雷的空间姿态,在鱼雷动力学中称为姿态角,其定义如下:
(1)俯仰角:雷体纵轴与地面的夹角(即与轴与其在地平面的投影线 之间的夹角),鱼雷抬头为正。
(2)偏航角:轴在地平面的投影线与参考航向之间的夹角(即与之间的夹角),鱼雷向左(逆时针)偏航为正。
(3)横滚角:雷体立轴与包含鱼雷纵轴的铅垂面之间的夹角(即与平面之间的夹角),鱼雷向右滚动为正(从雷尾观察)。
2. 鱼雷重心的瞬时运动方向
鱼雷重心的瞬时运动方向,可用表示速度矢量v与地面坐标系之间相对位置的弹道倾角、弹道偏角和倾斜角来描述,其定义如下(参见图2—3):
(1)弹道倾角:重心速度矢量V(OX轴)与地平面之间的夹角,鱼雷上爬为正,下潜为负。
(2)弹道偏角:重心速度矢量V在水平面上的投影()与参考航向()之间的夹角,鱼雷向左倔航为正。
(3)倾斜角:升力轴OY(在纵对称面内)与包含鱼雷重心速度矢量v(OX轴)的铅垂平面()之间的夹角,OY轴在该平面之右为正(从雷尾观察)。
3.流体动力角
确定重心速度矢量v在雷体坐标系中的方向需要两个角度参数,称为流体动力角,其定义如下(图2—2):
(1)攻角;鱼雷重心速度矢量V(OX轴)在鱼雷直鳍平面(或对称平面)内的投影()与雷体纵轴(轴)之间的夹角,V的投影()在轴之下为正。
(2)侧滑角;鱼雷重心速度矢量V与雷体直鳍平面(或对称平面)之间的夹角,V处于直鳍平面(或对称平面)之右为正。
 电子发烧友App
电子发烧友App


























评论