鱼雷流体动力的主向量和力矩
鱼雷流体动力
在任何情况下,流体对鱼雷的作用力总是以某种规律连续分布于鱼雷表面的表面力。当然,这种分布规律是取决于许多因素的。
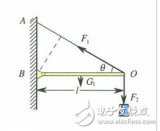
如图2-6所示,鱼雷表面上任一点处单位面积上流体的作用力可以分解为两个分量;与表面垂直的分量![]() (称为压力);与表面相切的分量(称为摩擦应力)。
(称为压力);与表面相切的分量(称为摩擦应力)。
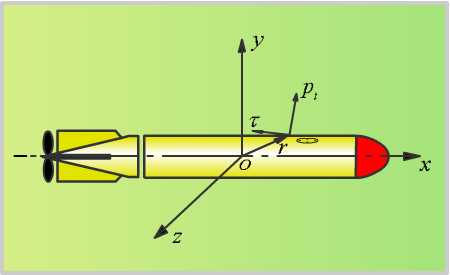
图2-6鱼雷表面受作用力
|
将这一表面力系简化至原点,可得流体动力的主向量和主矩为
|
式中 ——鱼雷表面任一点的向径;
![]() ——鱼雷的沾湿面积。
——鱼雷的沾湿面积。
容易理解,压力![]() 是由两部分组成的,即有
是由两部分组成的,即有
|
|
(2-3) |
式中 ![]() ——静水压力;
——静水压力;
![]() ——流体动力压力。
——流体动力压力。
这样,我们便有
|
|
(2-4) | |
|
|
(2-5) | |
| 或写成 |
|
(2-6) |
|
|
(2-7) | |
| 式中 |
|
(2-8) |
|
|
(2-9) | |
为由静水压力所形成的主向量和主矩。显然,它们正是鱼雷的浮力和浮力的主矩。
|
|
(2-10) |
|
|
(2-11) |
为流体动力压力和摩擦应力所形成的主向量和主矩。这部分主向量和主矩正是我们所要研究的对象。
将R和M写成速度坐标系内的投影形式:
|
|
(2-12) |
|
|
(2-13) |
式中![]() ——依次为沿x轴,y轴和z轴的单位向量;
——依次为沿x轴,y轴和z轴的单位向量;
![]() —阻力;
—阻力;
![]() —升力;
—升力;
![]() —侧力;
—侧力;
![]() —横倾力矩;
—横倾力矩;
![]() —偏航力矩;
—偏航力矩;
![]() —俯仰力矩。
—俯仰力矩。
同样,还可以写出R和M在雷体坐标系内的投影形式:
|
|
(2-14) |
|
|
(2-15)
|
式中![]() 称为纵向力,
称为纵向力,![]() 称为法向力,
称为法向力,![]() 称为侧向力;
称为侧向力;![]() 和
和![]() 依次与
依次与![]() 和
和![]() 同名。
同名。
实验和理论均可证明,在既定流体介质(水或空气)及介质温度的条件下,鱼雷的流体动力及力矩与鱼雷的流体动力外形,姿态(攻角及侧滑角![]() )和鱼雷的运动参数(速度、角速度,加速度及角加速度)等因素有关。由此,对既定鱼雷以法向力和俯仰力矩为例,可以写出
)和鱼雷的运动参数(速度、角速度,加速度及角加速度)等因素有关。由此,对既定鱼雷以法向力和俯仰力矩为例,可以写出
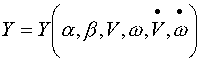 |
(2-16) |
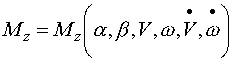 |
(2-17) |
在一般情况下,鱼雷的角速度,加速度及角加速度均比较小,我们可以利用泰勒级数展开的方法,将上述法向力和俯仰力矩写成如下线性关系式:
 |
(2-18) |
|
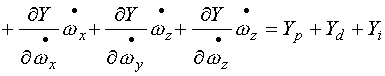 | ||
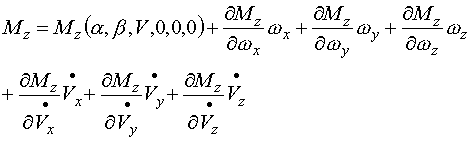 |
(2-19) |
|
 |
以上各导数均在![]() 出取值。
出取值。
| 在式中 |
|
(2-20) |
|
|
(2-21) |
为鱼雷以姿态角和![]() ,速度V做定常直线平移运动时的法向力和俯仰力矩。它们是该流体动力的主要成分,分别称为位置力和位置力矩
,速度V做定常直线平移运动时的法向力和俯仰力矩。它们是该流体动力的主要成分,分别称为位置力和位置力矩
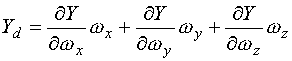 |
(2-22) |
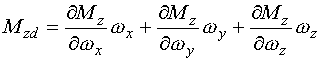 |
(2-23) |
为鱼雷由于旋转运动而引起的流体动力分量的增量,分别称为阻尼力和阻尼力矩。
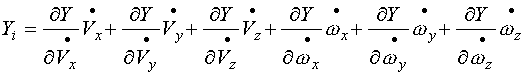 |
(2-24) |
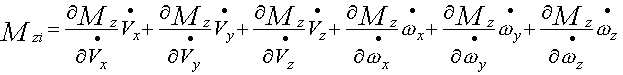 |
(2-25) |
为鱼雷由于其运动的不定常性而引起的流体动力分量的增量,称为非定常流体动力和力矩。
式(2-24)-(2-25)中的各个导数,按其自变量的性质分别称为某一流体动力分量对于该自变量的旋转导数,加速度导数或角加速度导数。例如:![]() 称为法向力对于
称为法向力对于 ![]() 的旋转导数;
的旋转导数;![]() 称为俯仰力矩对于
称为俯仰力矩对于![]() 的加速度导数;
的加速度导数;![]() 称为法向力对于
称为法向力对于![]() 的角加速度导数。
的角加速度导数。
以上,我们仅以法向力Y和俯仰力矩 为例得出上述表达式。对于其他流体动力分量,也可以得到类似的表达式。这样,我们共有6个位置力分量,18个旋转导数,18个加速度导数和18个角加速度导数。上述各量的确定,便最终的确定了鱼雷的流体动力和力矩。
 电子发烧友App
电子发烧友App













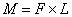

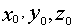










评论