图像缩放是数字图像处理中常用的技术之一。随着数字媒体的普及,图像缩放算法变得越来越重要。本文将探讨图像缩放的原理,着重介绍两种常用的插值算法——最近邻插值和双线性插值,并提供对应的代码实现。我们将解释这些算法的工作原理,以及如何选择最适合您应用场景的算法。 开发中可能非专业的开发人员外,其他人不会对其涉猎,但是图像的缩放这个话题确实值得我们学习和研究。 图像包含图片和视频,当你看视频时全屏变小窗,小窗变大屏等都用到了图像缩放,就视频而言,不同分辨率的切换也用到了缩放算法,比如,电影分辨率是 1080P,播放器的窗口大小是720P,则需要将电影画面从1080P缩小到720P再播放。如果你点击全屏播放,播放窗口变成了4K,则需要将电影画面做放大处理,即放大到4K之后再播放。
那图像缩放算法都有哪些呢?
他们的原理是什么?
在Android开发中怎么使用
图像缩放算法
图像缩放算法可以分为两类:插值算法和基于变换的算法。下面是一些常见的图像缩放算法:
最近邻插值算法(Nearest Neighbor Interpolation):最简单的插值算法,对于每个缩放后的像素点,选择与其最近的原始像素点的值作为它的值。该算法容易实现,但会导致图像出现锯齿状的边缘。
双线性插值算法(Bilinear Interpolation):该算法在最近邻插值算法的基础上,加入了对相邻四个像素点的加权平均,使得图像边缘更加平滑。
双三次插值算法(Bicubic Interpolation):该算法在双线性插值算法的基础上,对相邻16个像素点进行加权平均,得到更加平滑的图像。
Lanczos插值算法(LanczosInterpolation):该算法使用了一种卷积方法,通过对像素点周围的采样点进行加权平均,得到缩放后像素点的值。该算法在保持图像细节的同时,会对图像进行轻微模糊。
Sinc插值算法(SincInterpolation):该算法基于信号处理中的Sinc函数,使用卷积方法对像素点进行加权平均。该算法在保持图像细节的同时,会对图像进行一定的模糊,但比Lanczos插值算法的模糊程度小。
基于变换的算法:除了插值算法,还有一些基于变换的算法,如双线性变换、双三次变换、图像金字塔等。这些算法会对原始图像进行一定的变换,再进行缩放。这些算法通常能够产生更高质量的缩放结果,但计算复杂度也更高。
这些算法已经在行业中有较多的资料和使用文献,我这里简单梳理一下他们的原理以及在Android中怎么使用这些算法。
缩放的原理
首先要明确一点就是图像的缩放就是将原图像的已有像素经过加权运算得到目标图像的目标像素。比如说,我们已有图像是720P的分辨率,称之为原图像,我们需要放大到1080P,我们称这个1080P图像是目标图像。目标图像在宽度方向上放大了1920 / 1280 = 1.5倍,高度方向上也放大了1080 / 720 = 1.5倍。 那怎么通过720的图像生成1080的图像呢?放大之后会不会存在间隙,这个间隙是否会导致图像“发虚”呢? 做法如下: 先将目标图像的像素位置映射到原图像的对应位置上,然后把通过插值计算得到的原图像对应位置的像素值作为目标图像相应位置的像素值。 这样操作之后是不是就没有间隙了。这就是插值算法要干的事了。1080P目标图像中的(0,0)位置就映射到720P原图像的(0,0)位置,取原图像(0,0)位置的像素值作为目标图像(0,0)位置的像素值。目标图像的(1,1)位置就映射到原图像中的(0.67,0.67)位置。最后,通过原图像已有像素插值得到(0.67,0.67)位置的像素值,并将该像素值作为目标图像(1,1)位置的像素值。下图中,显示了720p放大到1080p的图示和720p缩小到360p的图示。
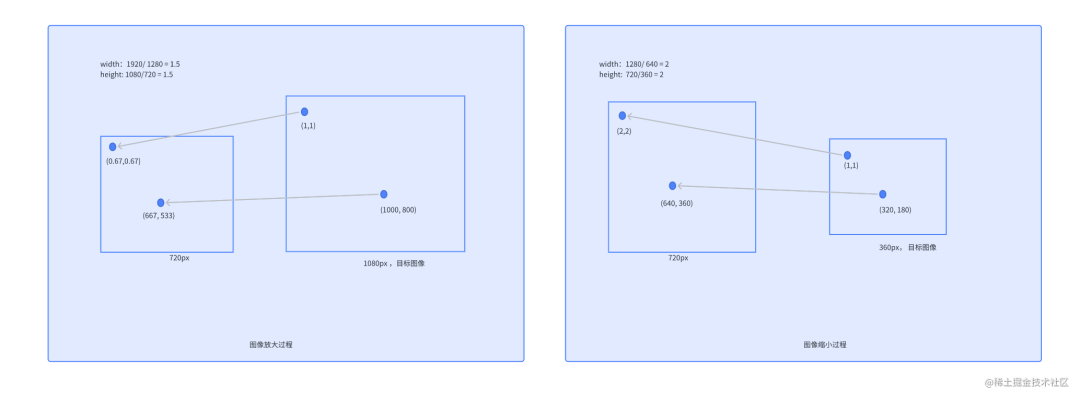
通过这个演示,可以总结一下图像缩放的一般过程:
放大过程对于1080P目标图像中的每一个像素点(x,y),我们只需要将它映射到 720P原图像的(x / 1.5,y / 1.5)位置,通过原图像已有的像素值插值得到(x / 1.5,y / 1.5)的像素值就可以了。
缩小过程对于360P目标图像中的每一个像素点(x,y),我们只需要将它映射到720P原图像的(x * 2,y * 2)位置,通过原图像已有的像素值插值得到(x * 2,y * 2)的像素值就可以了。
然后二者的操作过程是,遍历一下目标图像中的每一个像素点位置,都能找到他们在原图像中的映射位置,并通过插值求出映射位置的像素值,这样就可以得到目标图像了 我们可以推测出,缩放的代码逻辑是:
获取目标图像的宽高;
然后获取获取像素,完成像素插值
将处理过的像素创建新的图像
不用着急,后面可以验证该推测。 缩放的通用表达式 假设原图像的分辨率是 w0 x h0,我们需要缩放到 w1 x h1。那我们只需要将目标图像中的像素位置(x,y)映射到原图像的(x * w0 / w1,y * h0 / h1),再插值得到这个像素值就可以了,这个插值得到的像素值就是目标图像像素点(x,y)的像素值。注意,(x * w0 / w1,y * h0 / h1)绝大多数时候是小数。这就是图像缩放算法原理的通用表达示图如下:
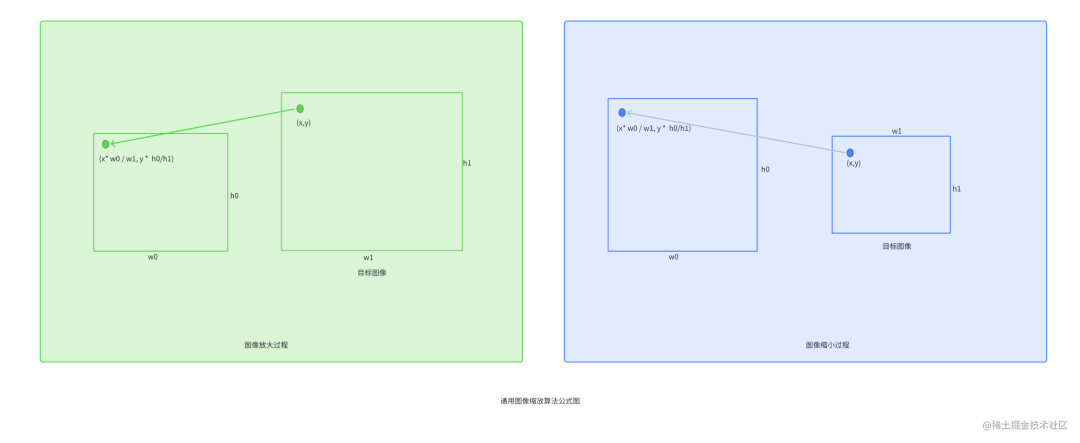
目前比较流行的插值算法基本有三种。
插值算法
最近邻插值算法 最近邻插值算法是一种基本的图像插值算法,它的基本思想是对于待插值像素的位置,选择距离该位置最近的一个已知像素值作为插值结果。因此,该算法得名为“最近邻插值”。 最近邻插值算法的具体实现过程如下:
确定待插值像素位置,假设其坐标为(x,y)。
找到离(x,y)最近的已知像素,假设其坐标为(x1,y1)。
将该已知像素的像素值赋值给待插值像素。
还是看图像从720p放大到1080p,这个例子,我们上面说了缩放的原理就是映射像素,即将目标图像的像素映射到原图像。 1080p假设(2,2)的位置,最邻近插值法的取值过程是: 映射到720P图像,映射位置是(2 * 1280 / 1920,2 * 720 / 1080),也就是(1.33,1.33)位置,其周围4个像素分别是(1,1)、(1,2)、(2,1)和(2,2),很明显(1,1)离(1.33l,1.33)位置最近,那我们取原图像(1,1)的像素值赋值给1080P图像的(2,2)位置的像素点。

左图为放大过程,右图为放大时取值图示:
所以1080待插值的位置(2,2)
找到了离(2,2)最近的已知像素(1.33,1.33)
将(1.33,1.33)位置的像素赋值给(2,2),完成插值。
代码实现
Java代码开发
最近邻插值算法java代码_图像最近邻插值算法_异域拾荒人的博客-CSDN博客
https://blog.csdn.net/weixin_32024145/article/details/114813888
使用Android JNI开发
使用opencv 库开发,因为需要获取像素等操作,最核心的代码为:
// 根据缩放比例计算输出图像的宽高 int new_width = static_cast
于其只考虑最近邻像素的值,而忽略了其他像素的信息,因此会导致图像插值后的结果较为粗糙,缺乏细节和平滑性
直接使用离插值位置最近的整数位置的像素作为插值像素,这样会导致相邻两个插值像素有很大的概率是相同的
应用场景
快速预览图像或图像缩小等场景。
双线性插值算法
双线性插值算法是一种常用的图像插值算法,它能够通过对周围4个已知像素进行加权平均来计算待插值像素的像素值,从而获得更为平滑和细腻的插值结果。听着就比最近邻插值算法复杂,但是效果肯定比它优。 双线性插值算法的具体实现过程如下: 确定待插值像素位置,假设其坐标为(x,y)。找到距离(x,y)最近的四个已知像素,假设它们的坐标为(x1,y1)、(x2,y2)、(x3,y3)、(x4,y4)。计算待插值像素的像素值。假设待插值像素的像素值为f(x,y),则可以通过下面的公式计算:
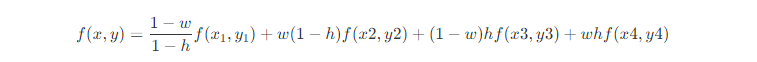
其中,w和h分别表示待插值像素相对于(x1,y1)和(x2,y2)的水平距离和垂直距离,具体计算方式如下:
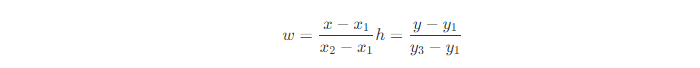
将计算得到的像素值赋给待插值像素。 线性插值 线性插值是一种数学方法,用于在两个已知点之间估计未知点的值。它假定两个已知点之间的函数是线性的,因此可以使用直线方程来计算未知点的值。 线性插值认为,这个需要插值得到的点跟这两个已知点都有一定的关系,并且,待插值点与离它近的那个点更相似。因此,线性插值是一种以距离作为权重的插值方式,距离越近权重越大,距离越远权重越小。 比如,如下图所示,已知 (x1,y1)与(x2,y2)两个点,需求得x对应的y值。
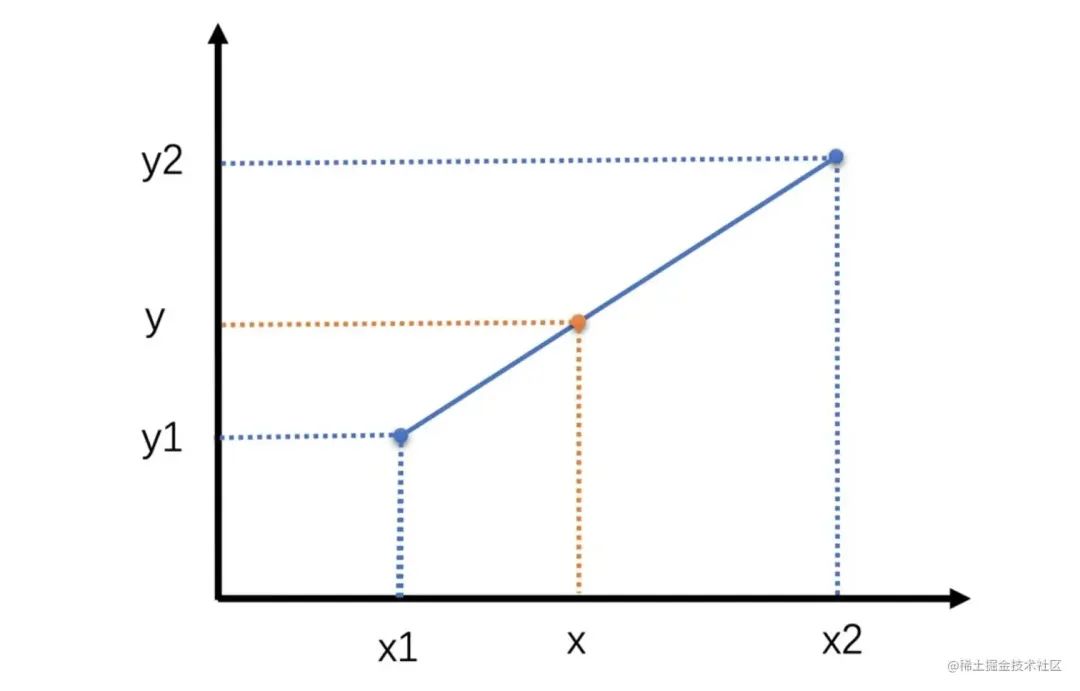
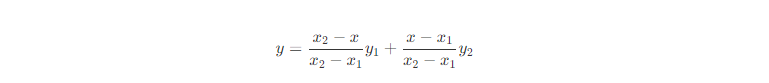
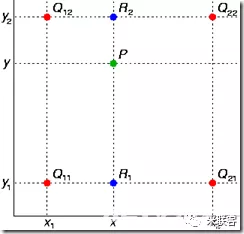
它表示在两个点(x1,y1)和(x2,y2)之间,对于给定的x值,对应的y值可以通过这个公式计算得到。当x=x1时,y=y1;当 x=x2 时,y=y2。当x在x1和x2之间时,y 的值在y1和y2之间线性变化。 双线性插值 双线性插值本质上就是在两个方向上做线性插值。由于图像是两个方向的二维数据,正好适合使用双线性插值算法。双线性插值其实就是三次线性插值的过程,我们先通过两次线性插值得到两个中间值,然后再通过对这两个中间值进行一次插值得到最终的结果。 假设我们有一个矩形网格,其中四个顶点的坐标分别为 (x1,y1),(x1,y2),(x2,y1) 和 (x2,y2),并且这些点的函数值分别为 f(x1,y1),f(x1,y2),f(x2,y1) 和 f(x2,y2)。我们想要计算点 (x,y) 的函数值,其中 x 和 y 分别在 x1 和 x2 之间,在 y1 和 y2 之间。
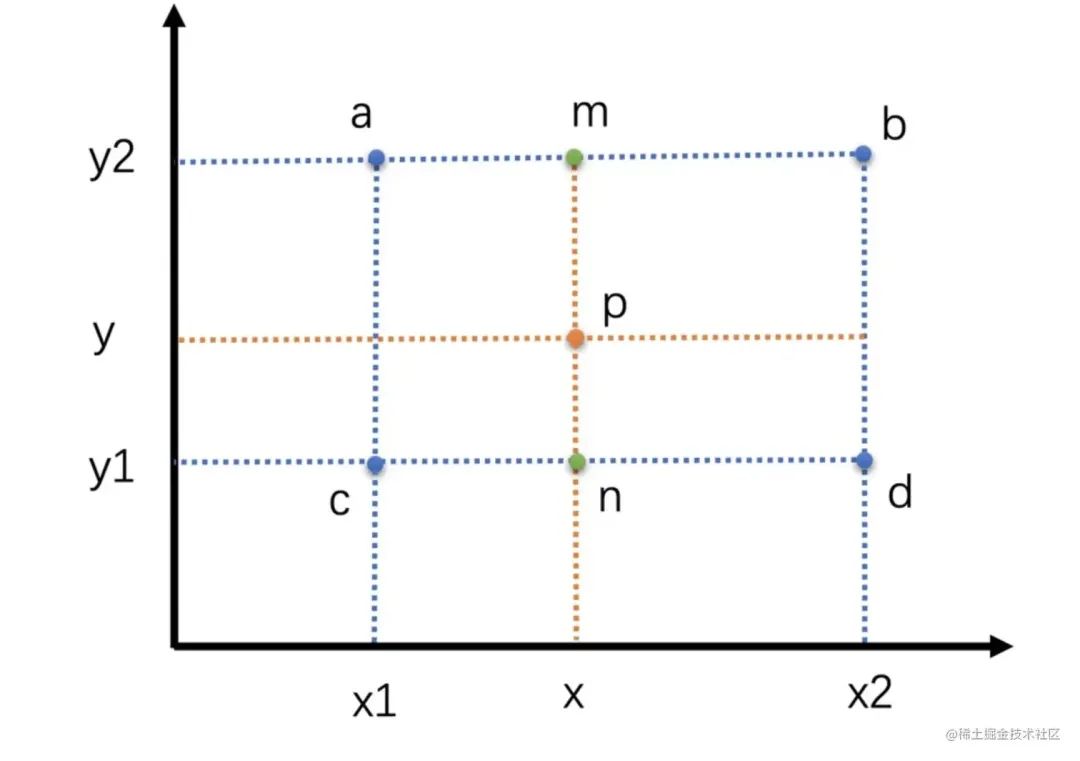
沿着x轴进行线性插值,得到两个临时值。
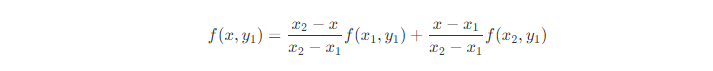
这个即图中的n点。
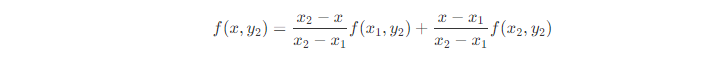
即图的m点,再沿着y轴线性插值。
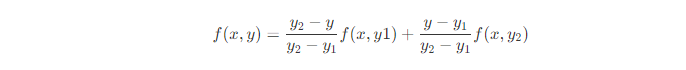
即图中p以720P放大到1080P为例,那么1080P图像中的目标像素点(2,2)的双线性插值过程是怎么样的呢? 首先,将目标像素点(2,2)映射到原图像的(1.33,1.33)位置,对应下面图中的点p。找到(1.33,1.33)周围的4个像素(1,1)、(2,1)、(1,2)和(2,2),分别对应图中的点a、b、c和d。
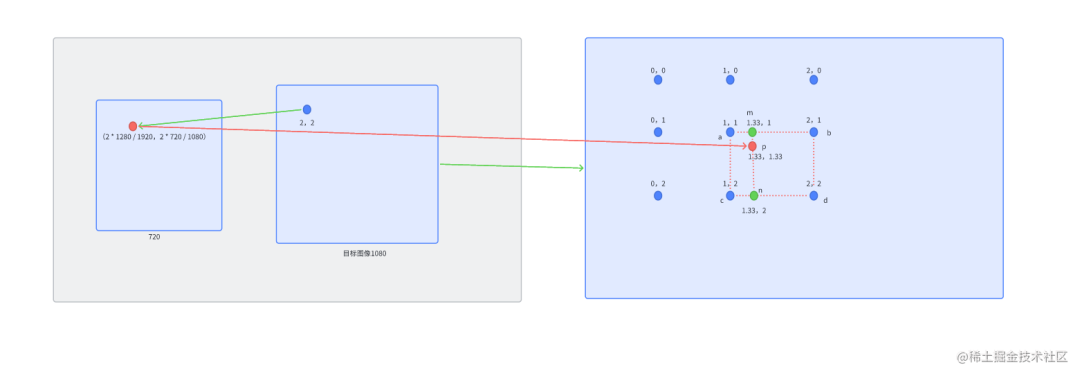
根据上述的公式,我们可以计算出图中的n、m 最后求出p 的像素。 首先n点:
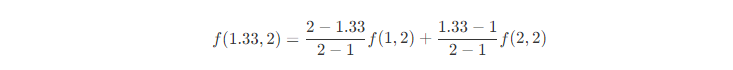
m点:
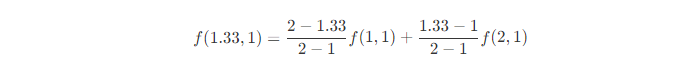
p点:
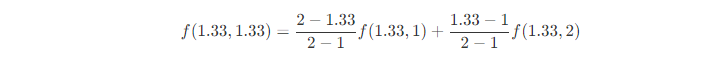
值求得(1.33,1.33)的值之后,将其赋值给1080P目标图像的(2,2)位置的像素点就可以了。这就是双线性插值的过程。 优缺点 优点:可以获得相对较为平滑和细腻的插值结果,而且计算速度也比较快 缺点:
只考虑了周围4个像素的信息,因此在图像放大的情况下,仍然会出现锯齿状的效果
在图像存在大幅度变化或复杂纹理的情况下,双线性插值算法可能会导致图像失真或出现马赛克效果
应用场景 图像放大、缩小和旋转等场景
总结
此文章主在弄明白图像缩放的原理,并完成了经典算法插值算法的最近邻插值算法,当然,最近邻插值算法的使用场景单一,也不是工作中常用的算法,后续会陆续完成双三次插值算法。双三次算法图像质量方面有明显提升,特别是在缩小图像时,双三次插值算法可以更好地保留图像的细节和纹理。
编辑:黄飞
 电子发烧友App
电子发烧友App

























评论