近年来,由于永磁同步电机(permanentmagnetsynchronousmotor,PMSM)高转矩电流比、效率高等优点,在伺服系统中得到广泛应用。随着人们对快速定位、调试简单等需求的增加,对伺服驱动器的控制技术提出了更高要求。因此PMSM构成的伺服系统的控制技术成为研究热点。针对永磁同步电机系统存在的负载转矩扰动和参数摄动等干扰,人们采用不同的思路进行解决。一方面,以经典的PID控制为基础,研究参数的在线调整。另一方面,智能控制技术、滑模变结构控制、预测控制、观测器等先进的控制理论也得到广泛地研究。
本文针对PMSM位置控制,提出一种基于自抗扰控制的双环控制方法。将ADRC引入到PMSM伺服系统的控制中,利用二阶非线性ADRC实现位置、速度的复合控制,从控制结构上将传统位置、速度、电流三环串级控制变为位置电流双环控制,可简化伺服系统的调试过程和提高动态响应速度。在建立伺服系统数学模型的基础上,给出位置环的二阶非线性ADRC、电流环一阶线性ADRC的设计方法,并对伺服系统的动态响应以及抗扰动性能进行研究。
一、ADRC抗干扰机理
ADRC之所以能够有效地提高系统的抗干扰能力,关键之处在于从被控输出量中提取干扰信号,并在控制律中进行扰动补偿。为了对系统中的扰动进行观测,需要设计扩张状态观测器,其以系统实际输出y和控制量u来跟踪估计系统的状态变量和扰动量,形式如下所示:

式中:z1, z2,…,zn为状态变量的观测值;zn+1为扰动估计值;β01, β02,…, β0(n+1)为观测器参数。
当φi(e)为线性函数时,ESO为线性观测器;而φi(e)具有非线性特性时,则为非线性观测器,通 过适当选择参数β来准确估计系统的状态变量和扰动值。
二、伺服系统自抗扰控制
1、伺服系统扰动分析
在同步旋转坐标系下,电磁转矩Te可表示为
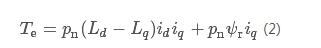
式中:pn为电机极对数;iq和id分别为交直轴电流;Lq和Ld为交直轴电感;ψr为转子磁链。运动方程为
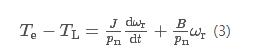
式中:TL为负载转矩;ωr为电角转速;J为转动惯量;B为粘滞摩擦系数。
在表贴式同步电机中有Ld=Lq,结合式(2)和(3),可建立以电角度θ和转子电角转速ωr为变量的二阶系统:
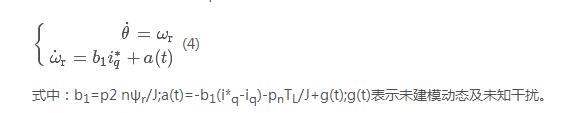
上述以iq为输入、电角度θ为输出的二阶系统,a(t)可视为位置控制回路的总扰动,包括q轴电流环控制误差,负载转矩、转子磁链、转动惯量等参数变化,g(t)表示的未建模动态等。
出现扰动时,依赖误差的传统反馈控制方法,只有在出现位置或速度偏差后才进行调节,必然存在一定程度上的滞后。为了实现高性能的控制,需要迅速抑制这些干扰对位置控制的影响,本文通过自抗扰控制器对系统中的扰动进行估计和补偿,提高系统的抗扰能力。
2、位移规划
伺服系统动态响应过快,可能会造成定位中出现超调。为了抑制在位置跟踪的过程中的超调,本文采用离散最速控制综合函数fhan构成的跟踪微分器进行位移规划,综合函数fhan表达式如下:
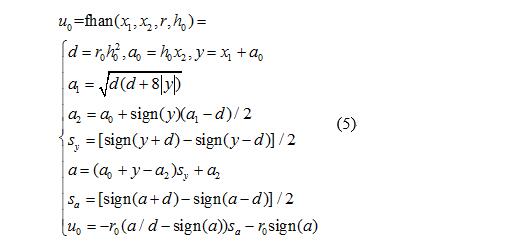
式中:x1和x2为输入变量;r和h0为调节参数;u0为函数输出值;其它为中间变量。
因此,位移规划如式(6)所示,参数h0取为位移规划的运算周期,通过唯一的参数r0调节位置指令跟踪的速度。这种位移规划方式不仅能够跟踪给定位置指令,并且对其中的噪声具有抑制作用。
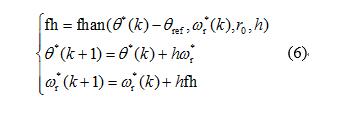
式中:θref为给定位置;θ*(k)和ω*r(k)分别是位置跟踪过程中第k个运算周期的的实际位置指令和速度指令,k≥0,稳态时有θ*=θref;h为位移规划运算周期;r0决定跟踪速度。
3、基于自抗扰的位置、速度复合控制
要实现ADRC,需要观测系统中的扰动,结合式(4),利用PMSM的电角度θ和q轴电流的给定值i* q来动态估计伺服系统的位置和扰动,三阶扩张状态观测器可以表示为
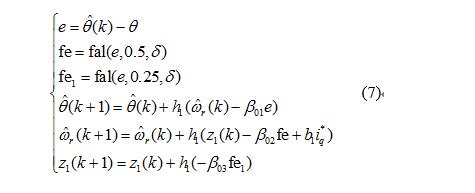
式中:θ^(k)θ^(k)和ω^r(k)ω^r(k)分别为第k个运算周期的电角
度θ和电角速度ωr的估计值,k≥0;e为观测误差;fal为非线性函数;z1为扰动量的观测值;β01、β02、β03为观测器系数;h1为位置环控制周期。
其中,
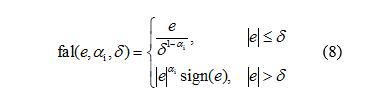
式中:δ为误差阈值;sign为符号函数;αi为参数。
fal函数具有“大误差,小增益;小误差,大增益”的特性;δ表示线性区间,目的是避免在误差较小时的高增益引起高频抖振。
上述非线性三阶扩张状态观测器的实现框图如图2中位置ESO所示,通过位置信息θ实时估计位置环的扰动z1,如负载转矩变化、系统惯量变化等,并将扰动以前馈的方式补偿到系统中,提高系统的干扰抑制能力。
为了使位置环具有较高的抗扰调节效率,误差反馈律采用如下式(9)的非线性控制律,包括位置误差、速度误差的反馈通道和扰动z1的前馈通道。利用一个环路实现位置和速度的复合控制,设计位置环时,不受速度环带宽的限制,不仅简化了控制结构,也便于系统的参数整定。
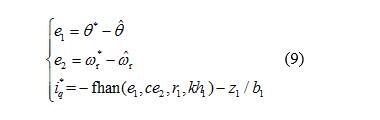
式中:b1=p2 nψr/J;c、r1和k为控制参数;h1为位置环控制周期;fhan函数详见式(5)。
参数r1为控制增益,当系统误差较大时,适当增大r1取值,误差趋于零的速度加快。在速度误差前引入参数c,调节复合控制中对速度控制作用的强弱。图1给出了r=3.5,h1=0.001,k=1000,c分别取1和6时的fhan函数的等高线。可以看出,随着参数c的增加,fhan函数输出量的线性调节区域减小,增大了对速度控制的作用。但这并不意味着r1和c的取值越大越好,因为过大的控制增益可能引起稳态时的高频抖振,此时需适当增大k的取值。
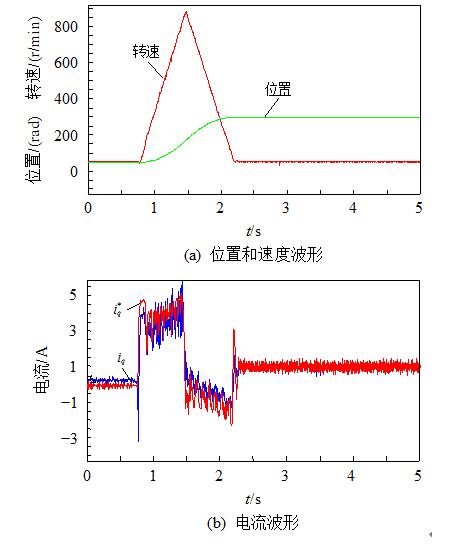
图1 r=3.5,不同c值时的fhan函数的等高线
因此,基于非线性自抗扰控制的位置、速度复合控制框图如图2所示。给定位置θref经过位移规
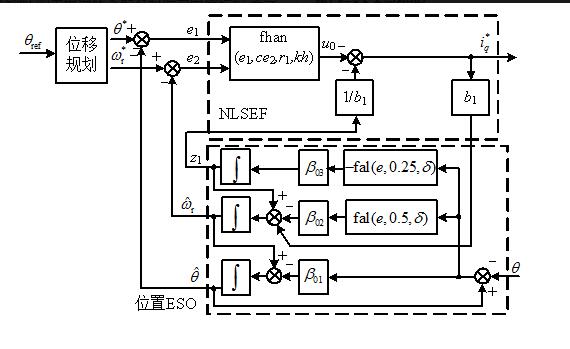
图2 位置、速度复合控制的结构图
划产生位置和速度参考,与扩张状态观测器的估计值运算,经过非线性的控制律,得到q轴电流的给定值。
因此,基于非线性自抗扰控制的位置、速度复合控制框图如图2所示。给定位置θref经过位移规划产生位置和速度参考,与扩张状态观测器的估计值运算,经过非线性的控制律,得到q轴电流的给定值。
4、电流环自抗扰控制
伺服系统中,当负载转矩出现扰动时,如果电流环不能及时调节电磁转矩,将导致位置出现较大偏差,对伺服系统的性能有很大的影响。
基于转子磁场定向矢量控制,采用id=0的控制时,q轴方程可以表示为
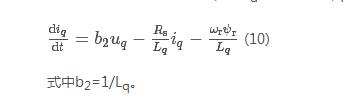
当负载变化时,将引起转速ωr的波动,而式(10)中,-ωrψr/Lq变化可以看作是干扰项,同时电阻Rs和电感Lq的参数摄动也可以看作q轴电流环的扰动。于是采用一阶ADRC算法,通过对转速引起的干扰项进行及时抑制,使对位置环的影响很小。为便于参数设计以及工程整定,观测器取为二阶线性状态观测器:
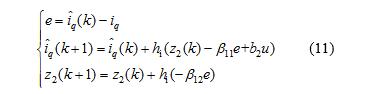
式中:i^q(k)i^q(k)为第k个运算周期的q轴电流iq估计值,
k≥0;z2为扰动量观测值;β11、β 12为电流观测器系数;hi为电流环运算周期。
如前文所述,ESO的性能对于扰动观测有较大影响,一种有效的选择线性ESO参数的方法是利用带宽的概念[20]。电流环带宽取为ωi,电流环ESO的特征多项式为s2+ β11s+β12,为了较好的估计状态和扰动,令其为理想的特征方程形式(s+ωi)2,于是参
数β11=2ω,ωiβ12=ω2iωi2。
电流环采用线性误差反馈率,如下:
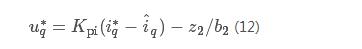
其中Kpi为电流控制增益。
因此,电流环的一阶ADRC的框图如图3所示。扩张状态观测器在观测电流的同时,给出系统的扰动量z2,经过补偿从而提高系统抗扰动的能力。
基于自抗扰控制的PMSM双环伺服驱动系统结构如图4所示。采用i* d=0控制方式,位置二阶ADRC控制器调节转矩电流给定值i* q,转矩电流的一阶ADRC控制器和励磁电流PI调节器调节相应的d、q轴定子电压给定值。
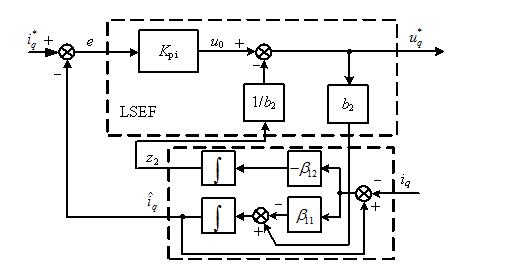
图3 电流iq一阶ADRC结构图
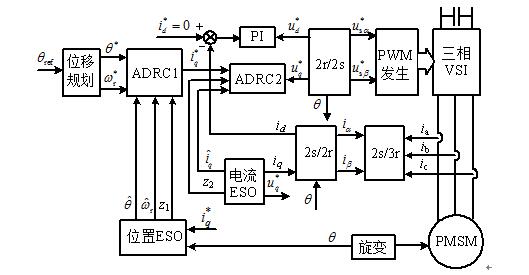
图4 基于自抗扰控制的双环伺服系统控制框图
三、仿真研究
仿真及实验用永磁同步电机参数如下:额定转速nN=2000r/min;定子电阻Rs=0.212Ω;交直轴电感Ld=Lq=3.2mH;转动惯量J=0.0176kg•m2;极对数pn=4;转子磁链ψr=0.199T。直流母线供电电压为150V,电流环的控制周期为200μs,位置环控制周期为1ms。
1、扩张状态观测器性能验证
给定位置θref=251.2rad时,位置和转速的仿真波形如图5所示。可以看出,系统在稳态和动态跟踪的过程中,都能准确地观测出位置、转速,表明设计的扩张状态观测器具有较高的观测精度。
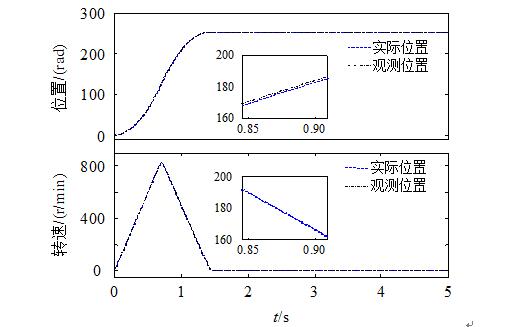
图5 定位过程中位置及速度仿真波形
2、位置环参数对控制性能影响验证
给定位置θref=251.2rad时,位置环参数r=3.5,c分别取1和6时的仿真波形如图6所示。当c=1时,最大值为251.52rad,系统出现了超调,而c=6时则无超调且响应时间更短,从转速下降时放大波形可以看出,c取6时转速跟踪特性更好,验证了2.3节的理论分析,表明引入控制参数c能够改变非线性反馈控制律的控制作用,通过选取合适的值能够提高系统的控制性能。
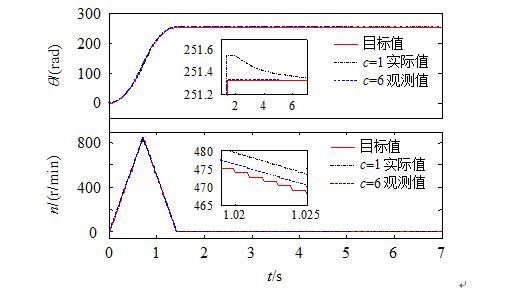
图6 参数c不同取值时的位置跟踪仿真波形
3、抗负载转矩扰动
动态跟踪过程中突加负载的仿真波形如图7所示。给定位置θref=251.2rad,在1s时突加5N•m的负载,转速最大跌落为20r/min,经过40ms跟踪上给定速度,而位置无明显波动。
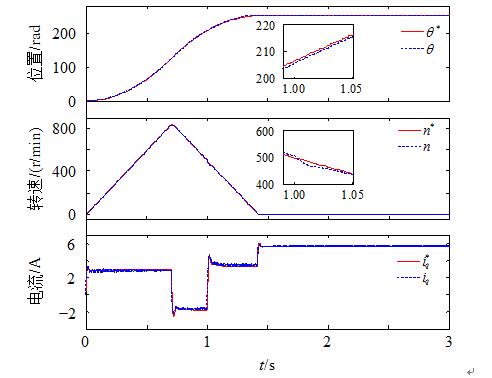
图7 动态跟踪过程中突加5N•m负载仿真波形
系统稳态时突加负载波形如图8,在3s时突加5N•m的负载,转速最大跌落为18.7r/min,调节时间约为10ms,稳态时存在0.3rad的误差。动静态的仿真结果说明在突加负载时,系统依然是稳定的,且具有较好地快速性,验证了所提出的控制算法具有较强的抗负载扰动的能力。
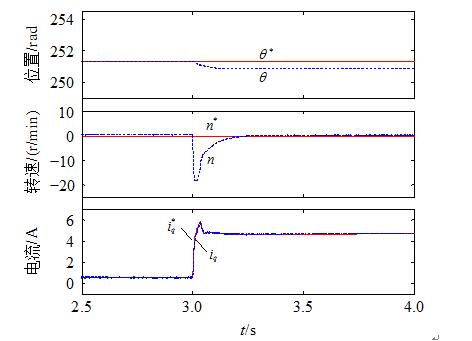
图8 稳态时突加5N•m负载仿真波形
4、电机参数失配时系统的鲁棒性
在电流环自抗扰控制器的设计中,观测器中存在参数b2=1/Lq,于是对电感Lq存在误差时系统的鲁棒性进行验证。图9给出当控制中所用的参数Lq为理想值的50%和200%时位置跟踪过程的仿真波形。结果表明即使在电感存在很大偏差的工况下,系统仍然稳定,扩张状态观测器仍能很好的观测电流iq,且能很好的跟随位置给定值的变化,表现出较好的抗参数变化的能力。
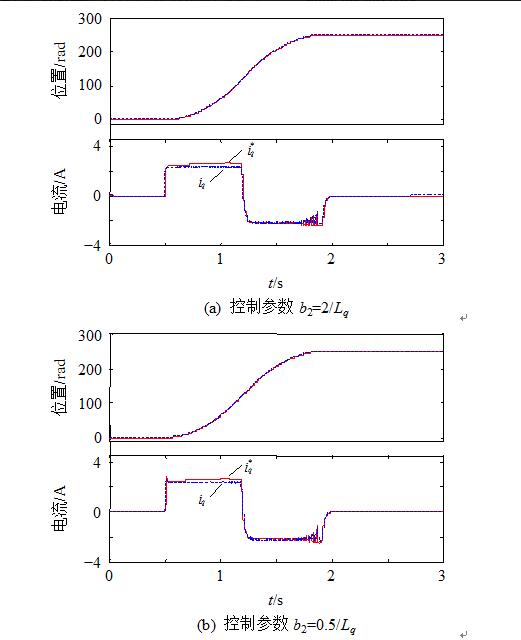
图9 Lq参数存在误差时定位仿真波形
四、实验结果
为了进一步验证所提控制策略,在dSPACE平台上进行实验,通过配套的ControlDesk上位机软件保存实验数据。
图10为给定位置θref=251.2rad时的实验波形。可以看出,在定位过程中,位置和速度均能能够很好地跟随目标值,稳态误差为0.4rad。
图11为给定位置θref=251.33rad时负载突变的
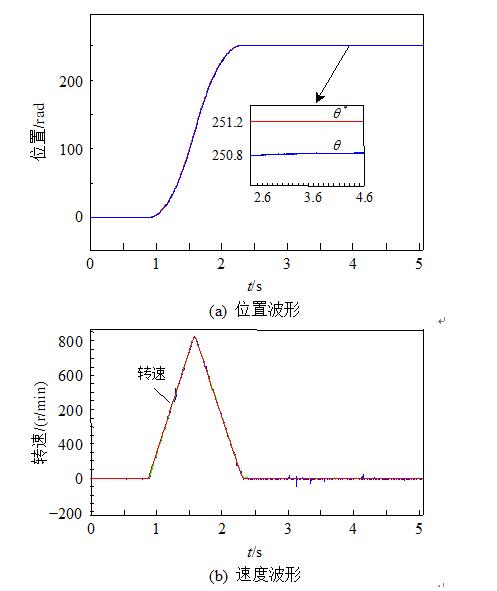
图10 定位过程中位置和速度实验波形
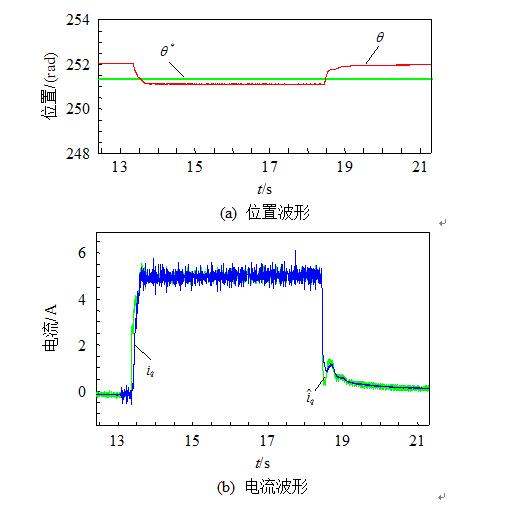
图11 负载突变实验波形
实验波形。在13.5s时刻从空载突加5s的5N•m的负载转矩扰动,空载时误差约为0.6rad,而带载5N•m后误差为0.2rad,在18.5s突变为空载时,系统依然稳定。
图12和13分别给出控制器中所用参数Lq为理想值的50%和200%时空载条件下的实验波形。即使采用不同的电感值,电机参数存在失配的工况下,电流iq稍有差异,但均达到了较好的位置跟踪效果。同时,从图中可以看出在最后到达稳态时,
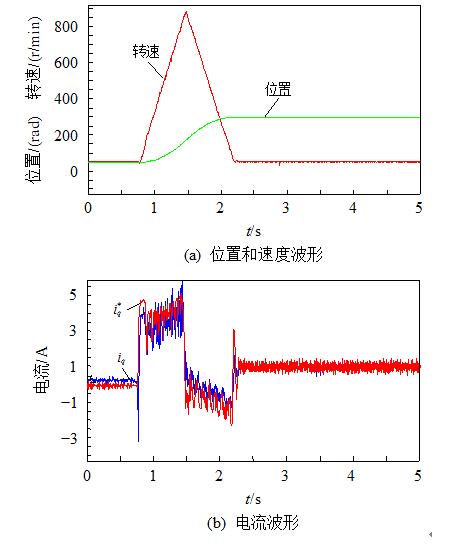
图12 控制参数b2=2/Lq定位波形
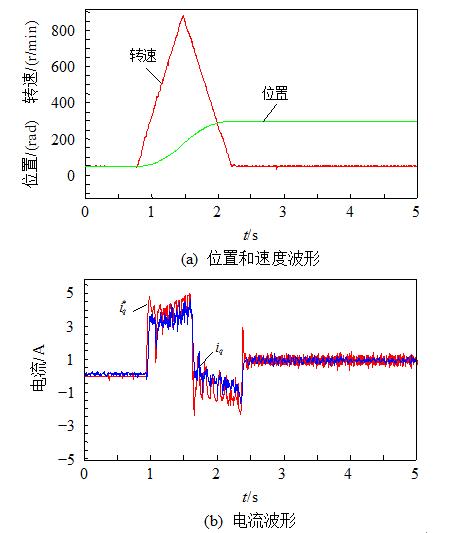
图13 控制参数b2=0.5/Lq定位波形
iq最终稳定在1A左右,而不是为0,这是由于稳态时电机转速接近零,但是位置ESO仍在进行观测,此时由于仍处在动态的调节过程中,电机的静摩擦转矩等未建模信息作为理想模型之外的扰动被估计出来,并补偿到电流环给定值i* q,使iq最终稳定在1A左右。
上述实验结果表明,提出的基于自抗扰控制的双环控制方法是正确的,提高了系统的抗负载转矩扰动的能力,同时在电机参数失配时仍具有较强的鲁棒性。
五、结论
本文从伺服系统抗干扰的角度出发,根据ADRC机理提出位置电流双环的自抗扰控制结构,给出了位置的二阶非线性自抗扰控制器和q轴电流的一阶线性自抗扰控制器的设计方法。仿真和实验结果表明本文提出的基于自抗扰控制的位置电流双环控制策略对负载转矩、电机参数变化等扰动的具有较好的抑制作用,说明该控制策略是一种行之有效的方法且具有工程应用价值
 电子发烧友App
电子发烧友App

























评论