基于Labview软件的雷达动目标显示和动目标检测

　　由于运动速度不同而引起回波信号频率产生的多普勒频移不相等，这就可以从频率上区分不同速度目标的回波，在动目标显示(MTI)和动目标检测(MTD)雷达中使用各种滤波器，滤除固定杂波而取出运动目标的回波，从而大大改善了在杂波背景下检测运动目标的能力.并且可以提高雷达的抗干扰能力。

　　1 Labview软件简介

　　Labview(Laboratory Virtual instrument Engineering)是一种图形化的编程语言，被工业界、学术界和研究实验室广泛接受，视为一个标准的数据采集和仪器控制软件。利用它可以方便地建立自己的虚拟仪器，其图形化的界面使编程及使用过程都生动有趣。

　　所有的Labview应用程序包括前面板(Front panel)、流程图(Block diagram)以及图标/连结器(Icon/connector)3部分。前面板(Front panel)是图形用户界面，也就是VI的虚拟仪器面板，这一界面上有用户输入和显示输出两类对象，具体有开关、旋钮、图形以及其他控制 (Control)和显示对象(Indicator);流程图(Block diagram)提供VI的图形化源程序，VI具有层次化和结构化的特征，一个VI可以作为子程序，称为子VI(SUBVI)，被其他VI调用;图标与连接器相当于图形化的参数。

　　2 信号源产生

　　该设计的首要问题是信号源的产生。产生一个正确合理的信号源直接关系到后面的一系列有关雷达信号处理的过程，因此信号源就显得十分关键。然而雷达信号有很多种，下面分别就等幅线性调频信号、不等幅线性调频信号以及二相码的产生进行介绍。

　　1)等幅线性调频信号

　　等幅线性调频矩形脉冲信号的复数表达式为：

　　

　　信号瞬时频率可以导出为

　　

　　式中，μ为fi的变化率，它与脉冲宽度τ和τ内的频率变化范围(又称频偏)B的关系为。

　　

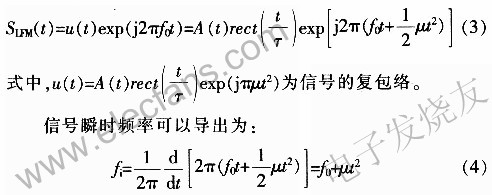
　　2)不等幅线性调频信号

　　不等幅线性调频矩形脉冲信号的复数表达式：

　　

　　式中，μ为fi的变化率，它与脉冲宽度τ和τ内的频率变化范围(又称频偏)B的关系。

　　3)二相码

　　一般相位编码(PCM)信号的复数表达式

　　

　　式中，u(t)=a(t)exp[jψ(t)]为其复包络，ψ(t)是相位调制函数，a(t)是幅度调制函数或称为PCM的包络。对二相码而言，ψ(t)∈{ψk=0，π}或表示为二进制序列{Cn=O，1，…，N-1}∈Ck={exp[jψ(k)]=+1，-l}。如果假设a(t)为矩形函数(亦可采用调幅)，即

　　式中，v(t)为所谓子脉冲函数，τc为子脉冲宽度，N为子脉冲数或码长，τ=Nτc是编码信号的持续期。

　　对于二相的巴克码序列，其码长N、自相关函数及主旁瓣比的关系如表1所示。

　　

　　3 动目标显示(MTI)

　　MTI(运动目标显示)的本质含义：基于回波多谱勒信息的提取而区分为运动目标和固定目标。当固定目标、地杂波与运动目标处于同一距离单元时，前者的回波通常比较强，以至于运动目标的回波被“淹没”其中，故必须设法区分二者。因固定目标回波中的多谱勒频率为零，慢速运动的杂波中所含的多谱勒频移也集中在零频附近，它们的回波经相位检波后，输出信号的相位将不随时间变化或随时间作缓慢变化，反映在幅度上则为其幅度不随时间变化或随时间作缓慢变化。相反，运动目标回波经相位检波后，因其相位随时间变化较大，反映在幅度上则为其幅度随时间变化较快。因此，若将同一距离单元在相邻重复周期内的相检输出作相减运算，则固定目标回波将被完全对消，慢速杂波也将得到很大程度衰减，只有运动目标得以保留。显然这样便可将固定目标、慢速杂波与运动目标区别开来。这就是MTI 对消的基本原理。

　　3.1 双脉冲对消

　　双脉冲对消又称一次对消，其对消公式y(n)=x(n)-kx(n-1)求Z变换则得y(Z)=X(Z)-KZ-1X(Z)，由此得到数字系统函数，将Z=exp(jΩTr)代入数字系统函数得频率响应为

　　

　　3.2 三脉冲对消

　　三脉冲对消又称二次对消，其对消公式为：y(n)=x(n)-kx(n-1)+x(n-2)，对其求Z变换则得：Y(Z)=(Z)-KZ-1(Z)+Z- 2X(Z)。由此可得到数字系统函数为H(Z)=l-KZ-1+Z-2，将Z=exp(jΩTr)代入得频率响应

　　

　　3.3 盲速处理

　　当fdTr=n(n=0，1，2，…)时，对消器输出为零，即当时，运动目标在对消器输出端无信号输出。这里当n=0即fd=O时，对应的固定目标无输出，这是所希望的。与此同时径向速度为零的动目标回波也会被抑制，这是不可避免的。但在n=1，2，3…时，具有这些多谱勒频率()的目标，在对消器输出端也没有输出，因此称对应这些多谱勒频率的目标径向运动速度为盲速，记为vro，即。可见盲速是目标在一个重复周期的位移恰好等于λ/2(或其整数倍)的速度。这时相邻周期重复周期的回波初相位差△φs。是2π(或其整数倍)，所以从MTI雷达相位检波器输出的视频脉冲幅度相等，故对消后△u=0。

　　4 动目标检测(MTD)

　　MTD与MTI虽同属雷达信号的频域处理范畴，但一般意义上说，MTD是MTI的改进或更有效的频域处理技术。实质上，MTD的核心就是线性DMTI加窄带多普勒滤波器组。实际情况中，多普勒频移不能预知，因此需要采用一组相邻且部分重叠的滤波器组，覆盖整个多普勒频率范围，这就是窄带多普勒滤波器组。

　　多普勒滤波器的实现方法：具有N个输出的横向滤波器(N个脉冲和N-l根延迟线)，经过个脉冲不同的加权并求和后，可以做成N个相邻的窄带滤波器组。该滤波器组的范围为0～fr，fr为雷达工作频率。横向滤波器有N-1根延迟线，每根延迟线的延迟时间为。设加在N个输出端头的加权值为

　　

　　式中，i表示第i个抽头;k表示0～(N-1)的标记，每个k值对应不同的加权值，相应地对应于一个不同的多普勒滤波器响应。由k表示的N个滤波器组成滤波器组，可写出横向滤波器按上式加权时的脉冲响应为：

　　

　　脉冲响应的傅里叶变换就是频率响应函数：

　　

　　滤波器振幅特性是频率响应取幅值。即

　　

　　滤波器的峰值产生于sin[π(fT-k/N)]=0或者π(fT-k/N)=0，π，2π，…;当k=0时，滤波器峰值位置为 f="0"，1/T，2/T，…，即该滤波器的中心位置在零频率以及重复频率的整数倍，这个滤波器通过没有多普勒频移的杂波，因此对地杂波没有抑制能力。然而，它的输出在某些MTI雷达中可以作提供杂波地图之用。这个滤波器的第1个零点是当上式分子第1次取零值时，或f=1/(NT)。在第1对零点之间的频带宽度为f=2/(NT)，而半功率带宽近似为0.9/(NT)。

　　5 数据仿真

　　根据上述提供的等幅线性调频信号模型和巴克码序列，利用Labview软件产生相应的等幅线性调频信号，三相编码，五相编码，七相编码信号。根据MTI和 MTD原理，对上述信号进行处理。从图1的仿真结果可以看出，经过MTI处理后，一些固定杂波(目标2，目标3，目标4)经过脉冲对消，匹配滤波，盲速处理，幅度明显减少，淹没在噪声中。运动目标信号明显出现在显示器上。改善因子是衡量MTI雷达工作质量的一个重要指标，定义为输出信号杂波功率比和输入信号杂波功率比之比值。经过上述MTD滤波器处理后，目标凸现。MTD滤波器组中8个滤波器对杂波的改善因子分别是 (58.6245，58.8137，58.8260，66.8277，68.0534，59.0719，58.5206，57.8894)。表2给出了在给定发现概率的情况下，使用MTD滤波器前后系统所需的信噪比，可以看出：对信噪比的要求有所降低，因此可以更好检测目标。

　　

　　

 

　　6 结束语

　　利用固定目标和运动目标之间速度的差别，所引起的多普勒频移不同。根据在动目标显示(MTI)和动目标检测(MTD)中使用的各种滤波器，去除固定杂波，提取动目标的回波，能够大大改善在杂波背景下检测运动目标的能力。仿真结果显示出很好的效果，也给出了改善因子与积累脉冲数之间的关系。可以看出 Labview软件在雷达信号处理方面提供了一个很好的平台，具有强大的函数库，使用方便，设计出的面板图直观，立体感较强。