电阻触摸屏的校准算法

　　为什么要校准

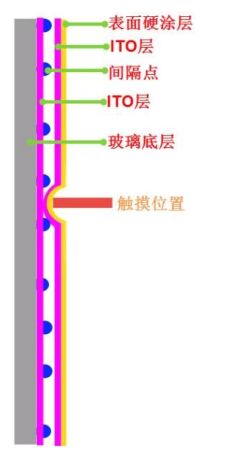
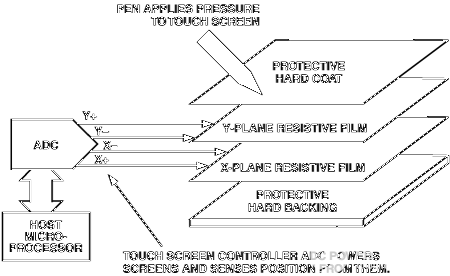
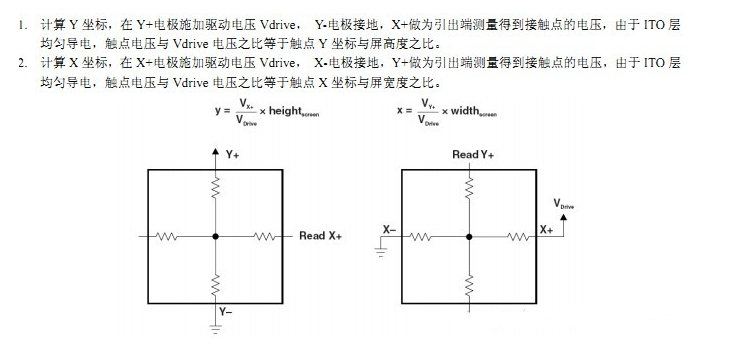
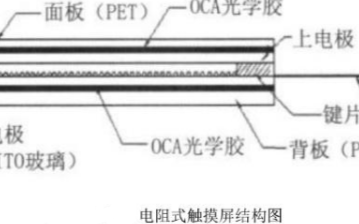
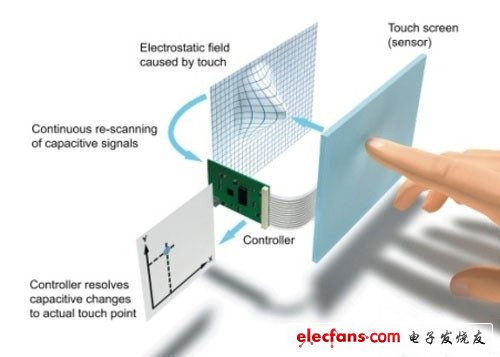
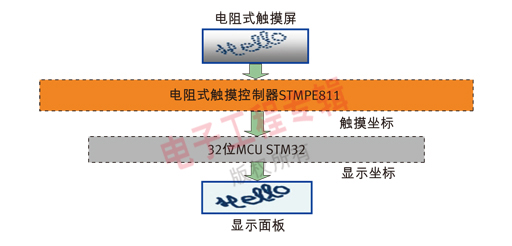
　　简单来说，电阻式触摸屏就是一种传感器，它利用压力感应进行控制，将矩形区域中触摸点（X，Y）的物理位置转换为代表X坐标和Y坐标的电压电阻式触摸屏的主要部分是一块与显示器表面非常配合的电阻薄膜屏，这是一种多层的复合薄膜，它以一层玻璃或硬塑料平板作为基层，表面涂有一层导电层（透明的导电电阻），上面再盖一层经过硬化处理光滑防擦的塑料层它的内表面也涂有一层透明导电层层，在他们之间有许多细小的（小于1/1000英寸）的透明隔离点把两层导电层隔开绝缘当手指触摸屏幕时，两层导电层在触摸点位置就有了接触，电阻发生变化，其中一面导电层接通Y轴方向的5V均匀电压场，使得侦测层的电压由零变为非零，控制器侦测到这个接通后，进行A/D转换，并将得到的电压值与5V相比即可得触摸点的Y轴坐标，同理也能得出X轴的坐标，然后再根据模拟鼠标的方式运作。

　　这就是所有电阻技术触摸屏共同的最基本原理由压力感应得到坐标值的并不能达到100%的精度，它存在着误差。由于误差的存在，在触摸屏上所绘制的图形和液晶屏上的图形，对应点的集合会有所偏差在触摸屏上点击某一按钮或选择某项功能时，内置的软件便无法对触摸屏上的点击做出正确响应，而触摸屏具有离散性，任意两个触摸点密度都不能完全一致，所以几乎所有带阻性触摸屏的设备在出厂前均要经过一定的校准校准是一种图形重建的过程，即将图形经过变换，换算出与液晶屏相一致的点集合，现有的校准算法主要是用来改善上述中的固有误差。

　　电阻触摸屏校准算法基本原理

　　1、基本概念

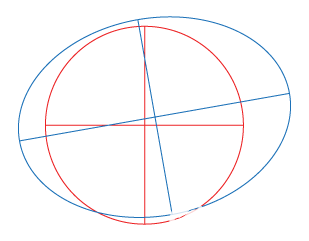
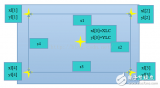
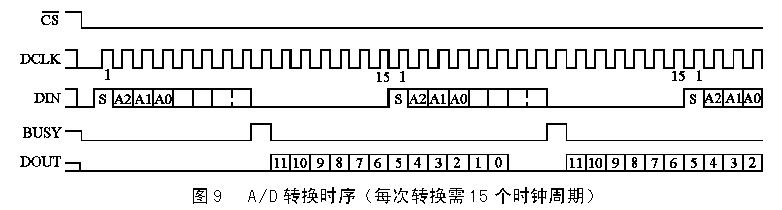
　　我们先引入两个概念，物理坐标和逻辑坐标。物理坐标指触摸屏上点的实际位置，通常以液晶上点的个数来度量。逻辑坐标指这点被触摸时A/D转换后的坐标值。如图1，我们假定液晶最左下角为坐标轴原点A，在液晶上任取一点B（十字线交叉中心），B在X方向距离A10个点，在Y方向距离A20个点，则这点的物理坐标为（10，20）。如果我们触摸这一点时得到的X向A/D转换值为100，Y向A/D转换值为200，则这点的逻辑坐标为（100，200）。

　　2、两点校准法

　　两点校准法即为取触摸屏成对角线的两个点来校准触摸屏。下面以取触摸屏左上角和右下角这两个点为例进行说明

　　1）先触摸并获取触摸屏左上角坐标（lefttop_x，lefttop_y）

　　2）再触摸并获取触摸屏右下角坐标（rightbottom_x，rightbottom_y）

　　3）计算触摸屏在水平方向和垂直方向的比率

　　Ratio_x=（rightbottom_x-lefttop_x）/触摸屏宽度

　　Ratio_y=（rightbottom_y-lefttop_y）/触摸屏高度

　　4）假设触摸屏当前点的坐标为（X，Y）

　　当前点X坐标=X*Ratio_x+lefttop_x

　　当前点Y坐标=Y*Ratio_y+lefttop_y

　　3、三点校准法

　　触摸屏常和点阵式液晶显示（LCD）屏叠加在一起配套使用，构成一个矩形的实际物理平面;而由用户触摸的触摸点集合经过A/D转换器，得到具体显示坐标的集合，这个集合构成了一个逻辑平面。由于存在误差，这两个平面并不重合，校准的作用就是要将逻辑平面映射到物理平面上，即得到触点在液晶屏上的位置坐标。校准算法的中心思想也就是要建立这样一个映射函数现有的校准算法大多是基于线性校准，即首先假定物理平面和逻辑平面之间的误差是线性误差，由旋转和偏移形成。如果已知触摸屏上一点A，其物理坐标为（xa，ya），相应的显示坐标为（xa’，ya’），根据假定的线性关系，可以得到：

　　Xa’=k1*xa+k2*ya+k3---------2-1

　　Ya’=k4*ya+k5ya+k6----------2-2

　　只要能够求出线性变换的参数（k1，k2…。）就可以来校正从触摸屏坐标得到显示坐标，显然要求参数，至少需要三个点的坐标，那么我们在触摸屏上取三个点（注意：不要取边界点，并且三点的覆盖面要大）

　　Xa’=k1*xa+k2*ya+k3---------2-1

　　Ya’=k4*ya+k5ya+k6----------2-2

　　Xb’=k1*xb+k2*yb+k3---------2-1

　　Yb’=k4*yb+k5yb+k6----------2-2

　　Xc’=k1*xc+k2*yc+k3---------2-1

　　Yc’=k4*yc+k5yc+k6----------2-2

　　通过高数上的各种算法，求出

　　Divider=（Xa’–Xc’）*（Yb’–Yc’）-（Xb’–Xc’）*（Ya’–Yc’）

　　（Xa-Xc）*（Yb-Yc）-（Xb-Xc）*（Ya-Yc）

　　k1=---------------------------------------------------

　　Divider

　　（Xa’–Xc’）*（Xb-Xc）-（Xa-Xc）*（Xb’–Xc’）

　　k2=-------------------------------------------------------------

　　Divider

　　Ya’*（Xc’*Xb–Xb’*Xc）+Yb’*（Xa*Xc’–Xc’*Xa）+Yc’*（Xb’*Xa–Xa’*Xb）

　　K3=--------------------------------------------------------------------------------------------------------

　　Divider

　　（Ya-Yc）*（Yb’–Yc’）-（Yb-Yc）*（Ya’–Yc’）

　　k4=----------------------------------------------------------

　　Divider

　　（Xa’-Xc’）*（Yb-Yc）-（Ya-Yc）*（Xb’–Xc’）

　　k5=----------------------------------------------------------

　　Divider

　　Ya’*（Xc’*Yb–Xb’*Yc）+Yb’*（Xa’*Yc–Xc’*Ya）+Yc’*（Xb’*Ya–Xa’*Yb）

　　K6=-----------------------------------------------------------------------------------------------

　　Divider

　　通过这几个参数，就可以算出物理坐标与显示坐标的对应关系。