电子发烧友App
前言
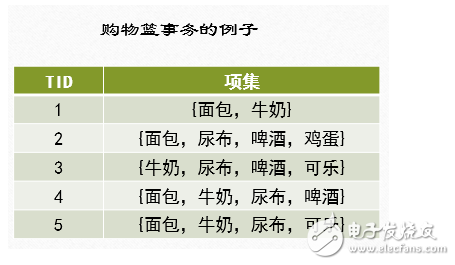
关联规则挖掘发现大量数据中项集之间有趣的关联或者相互联系。关联规则挖掘的一个典型例子就是购物篮分析，该过程通过发现顾客放入其购物篮中不同商品之间的联系，分析出顾客的购买习惯，通过了解哪些商品频繁地被顾客同时买入，能够帮助零售商制定合理的营销策略。购物篮事务的例子如下图所示：
例如：在同一次去超级市场时，如果顾客购买牛奶，同时他也购买面包的可能性有多大？
通过帮助零售商有选择地经销和安排货架，这种信息会引导销售。零售商有两种方法可以进行安排货架，第一种方法是将牛奶和面包尽可能的放的近一些，方便顾客自取，第二种方法是将牛奶和面包放的远一些，顾客在购买这两件物品的时候，这中间货架上的物品也会被顾客选择购买。这两种方法都可以进一步刺激消费。但是，如何发现牛奶和面包之间的关联关系呢？Apriori算法可以进行关联规则挖掘。
算法中的基本概念
1、项集和K-项集
令I={i1，i2，i3……id}是购物篮数据中所有项的集合，而T={t1，t2，t3….tN}是所有事务的集合，每个事务ti包含的项集都是I的子集。在关联分析中，包含0个或多个项的集合称为项集。如果一个项集包含K个项，则称它为K-项集。空集是指不包含任何项的项集。例如，在购物篮事务的例子中，｛啤酒，尿布，牛奶｝是一个3-项集。
2、支持度计数
项集的一个重要性质是它的支持度计数，即包含特定项集的事务个数，数学上，项集X的支持度计数σ（X）可以表示为
σ（X）=|{ti|X⊆ti，ti∈T}|
其中，符号|*|表示集合中元素的个数。
在购物篮事务的例子中，项集｛啤酒，尿布，牛奶｝的支持度计数为2，因为只有3和4两个事务中同时包含这3个项。
3、关联规则
关联规则是形如X→Y的蕴含表达式，其中X和Y是不相交的项集，即X∩Y=∅。
关联规则的强度可以用它的支持度（support）和置信度（confidence）来度量。支持度确定规则可以用于给定数据集的频繁程度，而置信度确定Y在包含X的事务中出现的频繁程度。
支持度（s）和置信度（c）这两种度量的形式定义如下：
s（X→Y）=σ（X∪Y）/N
c（X→Y）=σ（X∪Y）/σ（X）
其中， σ（X∪Y）是（X∪Y）的支持度计数，N为事务总数，σ（X）是X的支持度计数。
Example
在购物篮事务的例子中，考虑规则{牛奶，尿布}→{啤酒}。由于项集{牛奶，尿布，啤酒}的支持度计数为2，而事务的总数为5，所以规则的支持度为2/5=0.4。
规则的置信度是项集{牛奶，尿布，啤酒}的支持度计数与项集{牛奶，尿布}支持度技术的商，由于存在3个事务同时包含牛奶和尿布，所以规则的置信度为2/3=0.67。
关联规则发现
给定事务的集合T，关联规则发现是指找出支持度大于等于minsup （最小支持度）并且置信度大于等于minconf（最小置信度）的所有规则，minsup和minconf是对应的支持度和置信度阈值。
关联规则的挖掘是一个两步的过程：
（1）频繁项集产生：其目标是发现满足最小支持度阈值的所有项集（至少和预定义的最小支持计数一样），这些项集称作频繁项集。
（2）规则的产生：其目标是从上一步发现的频繁项集中提取所有高置信度的规则，这些规则称作强规则。（必须满足最小支持度和最小置信度）
Apriori算法介绍
Apriori算法的实质使用候选项集找频繁项集。
Apriori 算法是一种最有影响的挖掘布尔关联规则频繁项集的算法。算法的名字基于这样的事实：算法使用频繁项集性质的先验知识， 正如我们将看到的。Apriori 使用一种称作逐层搜索的迭代方法，k-项集用于探索（k+1）-项集。首先，找出频繁1-项集的集合。该集合记作L1。L1 用于找频繁2-项集的集合L2，而L2 用于找L3，如此下去，直到不能找到频繁k-项集。找每个Lk 需要一次数据库扫描。
Apriori性质
Apriori性质：频繁项集的所有非空子集都必须也是频繁的。 Apriori 性质基于如下观察：根据定义，如果项集I不满足最小支持度阈值s，则I不是频繁的，即P（I）《 s。如果项A添加到I，则结果项集（即I∪A）不可能比I更频繁出现。因此， I∪A也不是频繁的，即 P（I∪A）《 s 。
该性质属于一种特殊的分类，称作反单调，意指如果一个集合不能通过测试，则它的所有超集也都不能通过相同的测试。称它为反单调的，因为在通不过测试的意义下，该性质是单调的。
先验定理
先验定理：如果一个项集是频繁的，则它的所有子集一定也是频繁的。
（关于先验定理、单调与反单调可以参考下面的例子理解）
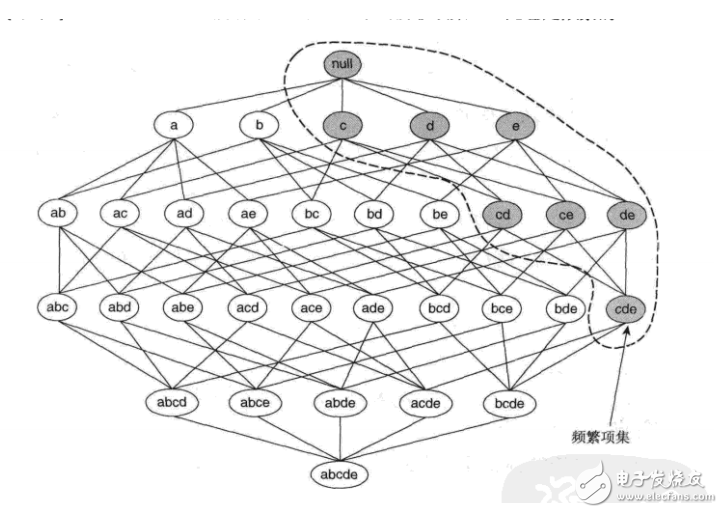
如图所示，假定｛c，d，e｝是频繁项集。显而易见，任何包含项集{c，d，e}的事务一定包含它的子集{c，d}，{c，e}，{d，e}，{c}，{d}和{e}。这样，如果{c，d，e}是频繁的，则它的所有子集一定也是频繁的。
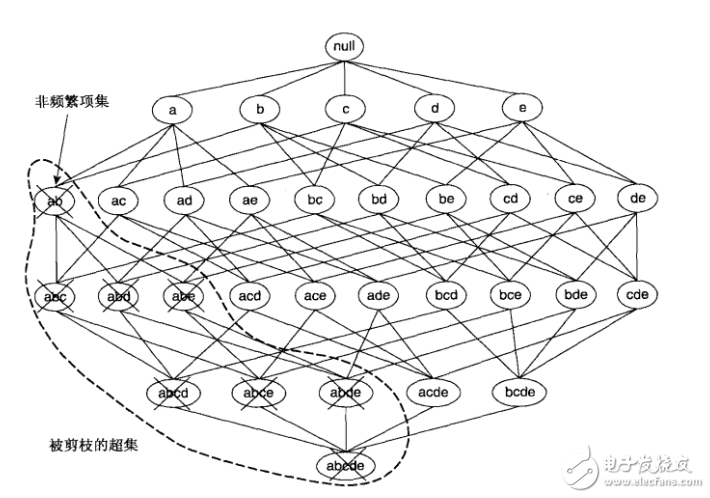
如果项集{a，b}是非频繁的，则它的所有超集也一定是非频繁的。即一旦发现{a，b}是非频繁的，则整个包含{a，b}超集的子图可以被立即剪枝。这种基于支持度度量修剪指数搜索空间的策略称为基于支持度的剪枝。
这种剪枝策略依赖于支持度度量的一个关键性质，即一个项集的支持度绝不会超过它的子集的支持度。这个性质也称支持度度量的反单调性。
挖掘频繁项集
Apriori算法的关键是如何用Lk-1找Lk？由下面的两步过程连接和剪枝组成。
连接步：为找Lk，通过Lk-1与自己连接产生候选k-项集的集合。该候选项集的集合记作Ck。设l1和l2是Lk-1中的项集。记号li［j］表示li的第j项（例如，l1［k-2］表示l1的倒数第3项）。为方便计，假定事务或项集中的项按字典次序排序。执行连接Lk-1 Lk-1；其中，Lk-1的元素是可连接的，如果它们前（k-2）个项相同；即，Lk-1的元素l1和l2是可连接的，如果（l1［1］=l2［1］）∧（l1［2］=l2［2］）∧…∧（l1［k-2］=l2［k-2］）∧（l1［k-1］《 l2［k-1］）。条件（l1［k-1］《 l2［k-1］）是简单地保证不产生重复。连接l1和l2产生的结果项集是l1［1］l1［2］…l1［k-1］l2［k-1］。
剪枝步：Ck是Lk的超集；即，它的成员可以是频繁的，也可以不是频繁的，但所有的频繁k-项集都包含在Ck中。扫描数据库，确定Ck中每个候选的计数，从而确定Lk（即，根据定义，计数值不小于最小支持度计数的所有候选是频繁的，从而属于Lk）。然而，Ck可能很大，这样所涉及的计算量就很大。为压缩Ck，可以用以下办法使用Apriori性质：任何非频繁的（k-1）-项集都不是可能是频繁k-项集的子集。因此，如果一个候选k-项集的（k-1）-子集不在Lk-1中，则该候选也不可能是频繁的，从而可以由Ck中删除。这种子集测试可以使用所有频繁项集的散列树快速完成。
Apriori算法
算法6.2.1（Apriori） 使用逐层迭代找出频繁项集
输入：事务数据库D；12345678910111213141516最小支持度阈值。
输出：D中的频繁项集L。
方法：
1） L1 = find_frequent_1_itemsets（D）; //找出频繁1-项集的集合L1
2） for（k = 2; Lk-1 ≠ ∅; k++） { //产生候选，并剪枝
3） Ck = aproiri_gen（Lk-1，min_sup）;
4） for each transaction t∈D{ //扫描D进行候选计数
5） Ct = subset（Ck，t）; //得到t的子集
6） for each candidate c∈Ct
7） c.count++; //支持度计数
8） }
9） Lk={c∈Ck| c.count ≥min_sup} //返回候选项集中不小于最小支持度的项集
10） }
11） return L = ∪kLk；//所有的频繁集
第一步（连接 join）
Procedure apriori_gen（Lk-1： frequent （k-1）-itemset; min_sup： support）
1） for each itemset l1∈Lk-1
2） for each itemset l2∈Lk-1
3） if（l1［1］=l2［1］）∧。..∧（l1［k-2］=l2［k-2］）∧（l1［k-1］《l2［k-1］） then{
4） c = l1 l2; //连接步：l1连接l2
//连接步产生候选，若K-1项集中已经存在子集c，则进行剪枝
5） if has_infrequent_subset（c，Lk-1） then
6） delete c; //剪枝步：删除非频繁候选
7） else add c to Ck;
8） }
9） return Ck;
12345678910111213
第二步：剪枝（prune）
Procedure has_infrequent_subset（c:candidate k-itemset; Lk-1:frequent （k-1）-itemset） //使用先验定理
1） for each （k-1）-subset s of c
2） if c∉Lk-1 then
3） return TRUE;
4） return FALSE;
1234567
由频繁项集产生关联规则
一旦由数据库D中的事务找出频繁项集，由它们产生强关联规则是直接了当的（强关联规则满足最小支持度和最小置信度）。对于置信度，可以用下式，其中条件概率用项集支持度计数表示。
confidence（A→B）=P（A│B）=support（A∪B）/support（A）
其中，support（A∪B）是（A∪B）的支持度计数，support（A）是A的支持度计数。
根据该式，关联规则可以产生如下：
ƒ 1、对于每个频繁项集l，产生l的所有非空子集。
ƒ 2、对于l的每个非空子集s，如果support（l）/support（s） ≥min_conf，则输出规则“s⇒（l-s）”。其中，min_conf是最小置信度阈值。
由于规则由频繁项集产生，每个规则都自动满足最小支持度。频繁项集连同它们的支持度预先存放在hash表中，使得它们可以快速被访问。
Apriori算法的实例
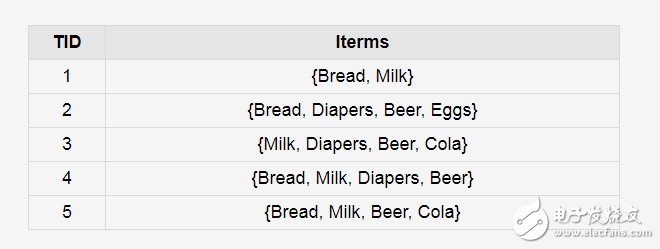
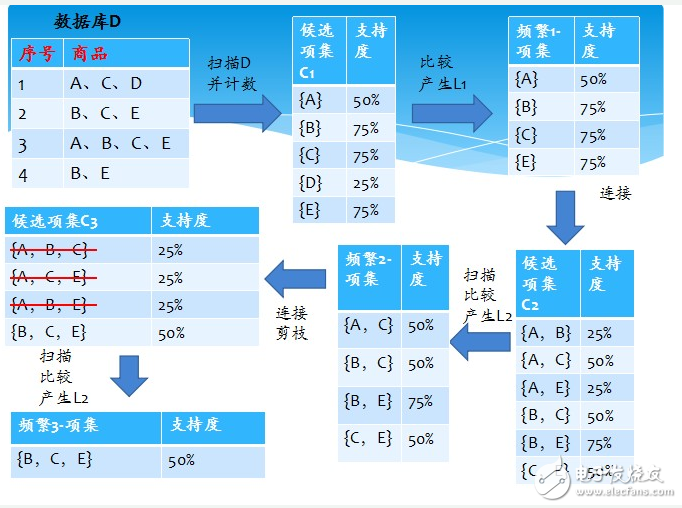
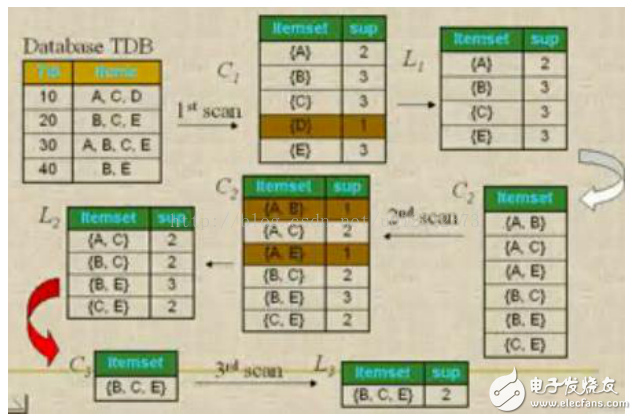
问题：数据库中有9个事务，即|D| = 9。Apriori假定事务中的项按字典次序存放。我们使用下图解释Apriori算法发现D中的频繁项集。 图四
分析与解：
（一）、挖掘频繁项集
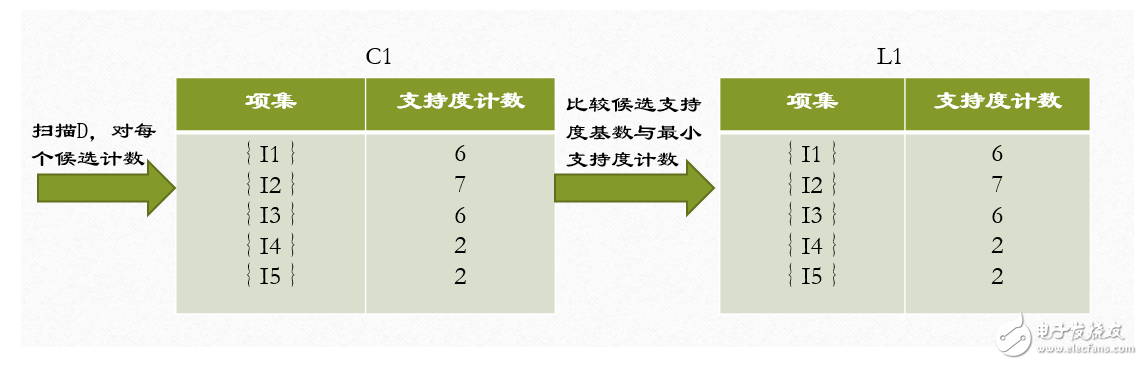
1、在算法的第一次迭代，每个项都是候选1-项集的集合C1的成员，算法简单地扫描所有的事务，对每个项的出现次数计数。
2、假定最小事务支持计数为2（即，minsup=2/9=22%）。可以确定频繁1-项集的集合L1。它由具有最小支持度的候选1-项集组成。
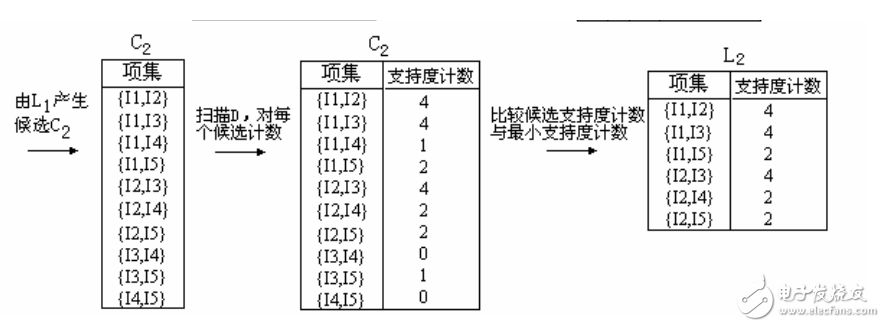
3、为发现频繁2-项集的集合L2，算法使用L1 L1产生候选2-项集的集合C2。
4、下一步，扫描D中事务，计算C2中每个候选项集的支持计数。
5、确定频繁2-项集的集合L2，它由具有最小支持度的C2中的候选2-项集组成。
【注】 L1 L1等价于L1×L1，因为Lk Lk的定义要求两个连接的项集共享k-1个项。
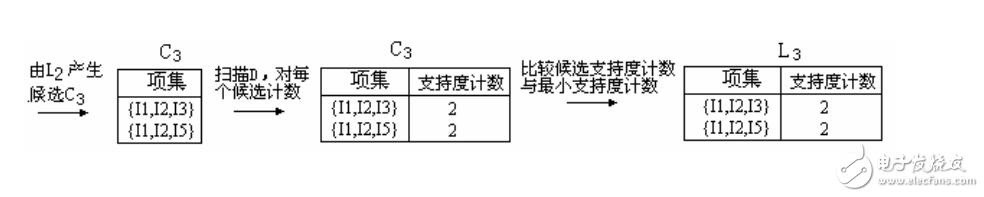
6、候选3-项集的集合C3的产生详细地列在图中。首先，令C3 = L2 L2 = {{I1，I2，I3}， {I1，I2，I5}， {I1，I3，I5}， {I2，I3，I4}， {I2，I3，I5}， {I2，I4，I5}}。根据Apriori性质，频繁项集的所有子集必须是频繁的，我们可以确定后4个候选不可能是频繁的。因此，我们把它们由C3删除，这样，在此后扫描D确定L3时就不必再求它们的计数值。注意，Apriori算法使用逐层搜索技术，给定k-项集，我们只需要检查它们的（k-1）-子集是否频繁。
【L2 L2连接生成C3的过程】
1．连接：C3= L2 L2={{I1，I2}，{I1，I3}，{I1，I5}，{I2，I3}，{I2，I4}，{I2，I5}} {{I1，I2}，{I1，I3}，{I1，I5}，{I2，I3}，{I2，I4}，{I2，I5}} = {{I1，I2，I3}，{I1，I2，I5}，{I1，I3，I5}，{I2，I3，I4}，{I2，I3，I5}，{I2，I4，I5}}
2．使用Apriori性质剪枝：频繁项集的所有子集必须是频繁的。存在候选项集，其子集不是频繁的吗？
ƒ{I1，I2，I3}的2-项子集是{I1，I2}，{I1，I3}和{I2，I3}。{I1，I2，I3}的所有2-项子集都是L2的元素。因此，保留{I1，I2，I3}在C3中。
ƒ{I1，I2，I5}的2-项子集是{I1，I2}，{I1，I5}和{I2，I5}。{I1，I2，I5}的所有2-项子集都是L2的元素。因此，保留{I1，I2，I5}在C3中。
ƒ{I1，I3，I5}的2-项子集是{I1，I3}，{I1，I5}和{I3，I5}。{I3，I5}不是L2的元素，因而不是频繁的。这样，由C3中删除{I1，I3，I5}。
ƒ{I2，I3，I4}的2-项子集是{I2，I3}，{I2，I4}和{I3，I4}。{I3，I4}不是L2的元素，因而不是频繁的。这样，由C3中删除{I2，I3，I4}。
ƒ{I2，I3，I5}的2-项子集是{I2，I3}，{I2，I5}和{I3，I5}。{I3，I5}不是L2的元素，因而不是频繁的。这样，由C3中删除{I2，I3，I5}。
ƒ{I2，I4，I5}的2-项子集是{I2，I4}，{I2，I5}和{I4，I5}。{I4，I5}不是L2的元素，因而不是频繁的。这样，由C3中删除{I2，I3，I5}。
3．这样，剪枝后C3 = {{I1，I2，I3}，{I1，I2，I5}}
7、扫描D中事务，以确定L3，它由具有最小支持度的C3中的候选3-项集组成。
8、算法使用L3 L3产生候选4-项集的集合C4。尽管连接产生结果{{I1，I2，I3，I5}}，这个项集被剪去，因为它的子集{I1，I3，I5}不是频繁的。这样，C4=∅，因此算法终止，找出了所有的频繁项集。
（二）、由频繁项集产生关联规则
假定数据包含频繁项集l={I1，I2，I5}，可以由l产生哪些关联规则？l的非空子集有{I1，I2}，{I1，I5}，{I2，I5}，{I1}，{I2}和{I5}。结果关联规则如下，每个都列出置信度。
I1∩I2→I5， confidence=2/4=0.5=50%
I1∩I5→I2， confidence=2/2=1=100%
I2∩I5→I1， confidence=2/2=1=100%
I1→I2∩I5， confidence=2/6=0.33=33%
I2→I1∩I5， confidence=2/7=0.29=29%
I5→I1∩I2， confidence=2/2=1=100%
如果最小置信度阈值为70%，则只有2、3和最后一个规则可以输出，因为只有这些才是强规则。
优缺点
优点
使用先验性质，大大提高了频繁项集逐层产生的效率；简单易理解；数据集要求低。
缺点
1、候选频繁K项集数量巨大。
2、在验证候选频繁K项集的时候，需要对整个数据库进行扫描，非常耗时。
改进算法
算法思想：
上面的原始算法中由Ck（Lk-1直接生成的）到Lk经过了两步处理，第一步根据Lk-1进行裁剪，第二步根据minsupport裁剪。上面提到的两个提高效率的方法都是基于第一步的。当经过联接生成K维数据项集时，判断它的K-1维子集是否存在于Lk-1中，如果不在直接删除。这样每生成一个K维数据项集时，就要搜索一遍Lk-1。改进算法的思想就是只需要搜索一遍Lk-1就可以了。当所有联接完成的时候，扫描一遍Lk-1，对于Lk-1任意元素A，判断A是否为Ck中元素 c的子集，如果是，对子集c进行计数。也就是统计Lk-1中包含Ck中任意元素c的K-1维子集的个数。最后根据c进行裁剪。c的计数，即 Lk-1中包含的c的子集的个数，小于K，则删除。
改进算法伪代码
算法的主体不变，aprriori_gen函数改变如下，函数 has_infrequent_subset不再需要。
procedure apriori_gen（Lk-1:frequent（k-1）-itemsets;minsupport:minimum support threshold）
（1）for each itemset l1 ∈ Lk-1
（2）for each itemset l2∈ L k-1
（3）if（l1［1］=l2［1］）∧（l1［2］=l2［2］）∧…∧（l1［k-2］=l2［k-2］）∧（l1［k-1］=l2［k-1］） then
（4）c=l1∪ l2;
（5）for each itemset l1∈ L k-1 //扫描Lk-1中的元素
（6）for each candidate c∈ Ck //扫描 Ck中的元素
（7）if l1 is the subset of Ck then //判断前者是不是后者的子集，如果是计数加1
（8）c.number++;
（9）C‘k={ c∈Ck |c.number=k};
（10）return C’k;
12345678910111213
例子对比：
问题：假设Lk-1={{1，2，3}，{1，2，4}，{2，3，4}，{2，3，5}，{1，3，4}}，求Lk。
由Lk-1得到Ck={{1，2，3，4}，{2，3，4，5}，{1，2，3，5}}。
原算法：首先得到{1，2，3，4}的子集{1，2，3}，{1，2，4}，{2，3，4}，{1，3，4}。然后判断这些子集是不是 Lk-1的元素。如果都是则保留，否则删除。这里保留，{2，3，4，5}和{1，2，3，5}则应该删除。得到C’k={{1，2，3，4}}。
改进算法：首先从Lk-1中取元素{1，2，3}，扫描Ck中的元素，看{1，2，3}是不是Ck元中元素的子集，{1，2，3}是{1，2，3，4}的子集，{1，2，3，4}的计数加1，{1，2，3}不是{2，3，4，5}的子集，计数不变，是{1，2，3，5}的子集，计数加1，经过对{1，2，3}处理后得到计数{1，0，1}；然后看{1，2，4}，{1，2，4}是{1，2，3，4}的子集，而不是 {2，3，4，5}的子集，也不是{1，2，3，5}的子集，计数不变，计数变为{2，0，1}；考察{2，3，4}，{2，3，4}是{1，2，3，4}的子集，也是{2，3，4，5}的子集，不是｛1，2，3，5｝的子集，计数变为{3，1，1}；{2，3，5}不是{1，2，3，4}的子集，是{2，3，4，5}的子集，也是{1，2，3，5}的子集，计数变为{3，2，2}；{1，3，4}是{1，2，3，4}的子集，不是{2，3，4，5}的子集，也不是{1，2，3，5}的子集，计数变为{4，2，2}。对数据扫描完毕。此时K=4，只有第一个元素的计数为4，为高频数据项集。得到C’k={{1，2，3，4}}。
复杂度对比
下面对原算法和改进算法的性能进行比较。Lk-1中的数据项集的个数记为|Lk-1|，Ck中的数据项集的个数记为|Ck|，Ck中元素的子集个数设为ni，其中i=1～|Ck| 。这里只分析从Ck～C’k的处理。原 算法从 AprioriCk中取元素，然后求该元素的子集，判断该子集是否在 |Ck|中。需要进行的计算为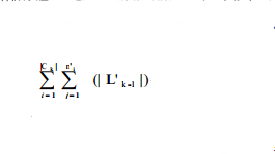 
次， 1<=|L’k-1|<=|L’k-1|，1<= n’i <=n i。而改进算法是从Lk-1中选取元素，看是不是Ck中元素的子集，对 Ck中数据项集的子集个数进行统计。需要进行的计算是（|Lk-1|+1）*|Ck| 次。如果 n’i =1，就是每次只取Ck中数据项集的一个子集就可以判断该数据项集，则两个算法的效率基本相同，但是这种情况很少出现，从而大部分情况下，改进算法的效率要高于原算法。
工商网监
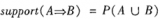
评论