RLC串联电路暂态特性的研究
电阻、电容及电感是电路中的基本元件, 在交流电路中,电阻值和频率无关,电容具有 “ 通高频、阻低频 ” 的特性 , 电感具有 “ 通低频,阻高频 ” 的特性 . 由 RC 、 RL 、 RLC 构成的串联电路具有不同的特性,包括暂态特性、稳态特性、谐振特性.它们在电子电路中有许多用途.本实验主要研究 RC 、 RL 、 RLC 电路的暂态特性 .
【预习要求】
1. 阅读大学物理中有关 RL 、 RC 、 RLC 电路的特点 .
2. 复习示波器实验 .
【实验目的】
1 .学习如何通过实验方法研究有关 RC 、 RL 和 RLC 串联电路的暂态过程 .
2 .通过研究 RC 、 RL 和 RLC 串联电路的暂态过程,加深对电容充、放电规律,电感的电磁感应特性及振荡回路特点的认识 .
【实验仪器】
信号发生器,双踪示波器,电阻箱, RLC 电路板
【实验要求】
1 .取不同参数的 RC 或 RL 组成串联电路,测量并描绘当时间常数小于或大于方波的半周期时的电容或电感上的波形,计算时间常数并与理论值比较;
2 .选择不同的 RLC 组成的串联电路,测量并描绘欠阻尼过程、临界阻尼过程、过阻尼过程时电容上的波形,计算时间常数并与理论值比较.
【实验提示】
一、原理设计
1 . RC 串联电路的暂态过程
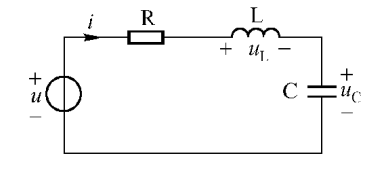
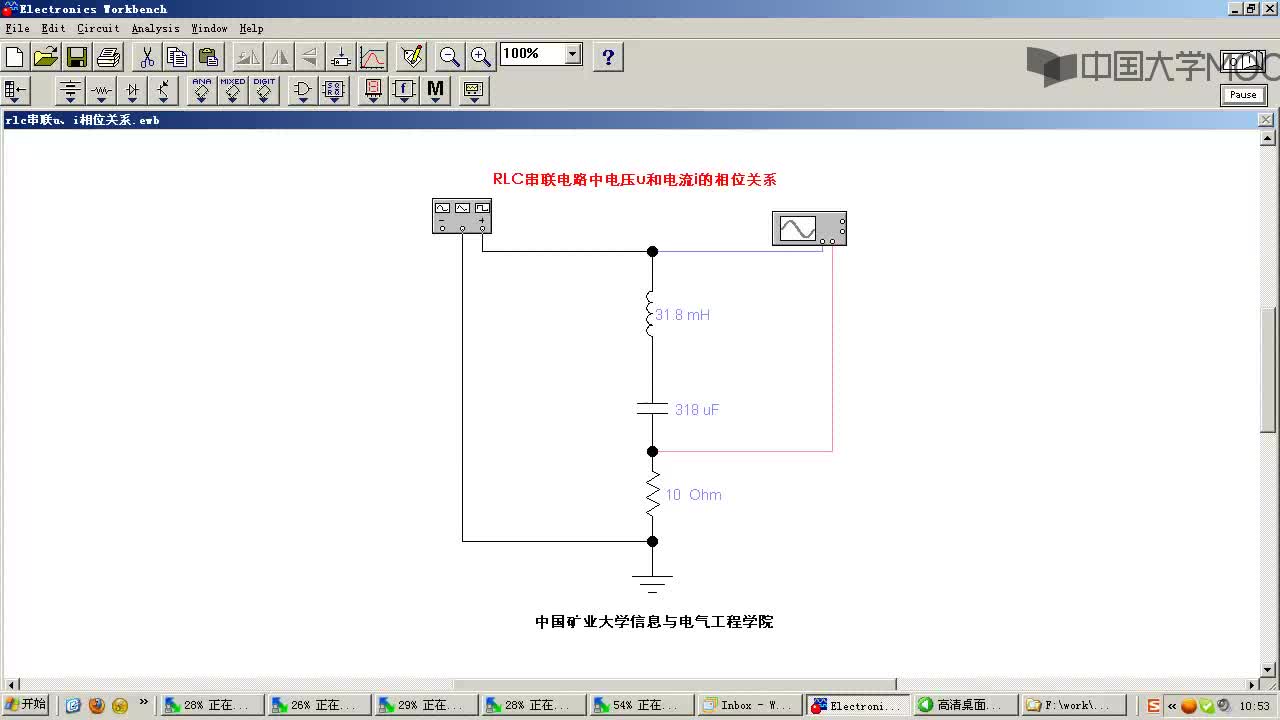
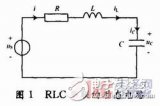
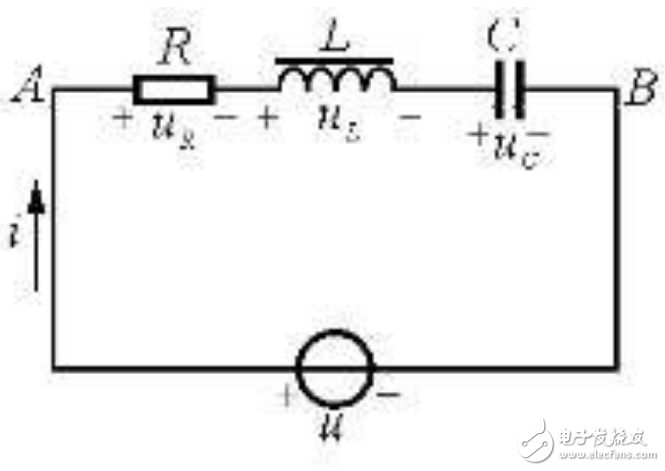
在由 R 、 C 组成的电路中,暂态过程是电容的充放电过程.图 29-1 为 RC 串联电路 .其中信号源用方波信号. 在上半个周期内,方波电压为 + E ,其对电容充电;在下半个周期内,方波电压为零,电容对地放电.充电过程中的回路方程为
( 29-1 )
由初始条件 t = 0 时, U C = 0 ,得解为
( 29-2 )
从 U C 、 U R 二式可见, U C 是随时间 t 按指数函数规律增长,而电阻电压 U R 随时间 t 按指数函数规律衰减,如 图 29-2 中 U – t 、 U C – t 及 U R – t 曲线 所示.
在放电过程中的回路方程为
( 29-3 )
由初始条件 t = 0 时, U C = E ,得解为
( 29-4 )
从 U C 、 U R 式可见,它们都随时间 t 按指数函数规律衰减.式中的 RC = t 具有时间的量纲,称为时间常数,是表征暂态过程进行快慢的一个重要物理量.与时间常数 t 有关的另一个另一个表征 RC 电路特征的值为半衰期 T 1/2 ,定义为当 U C ( t )下降到初值(或上升至终值)一半时所需要的时间,它同样反映了暂态过程的快慢程度,与 t 的关系为
T 1/2 = t ln2 = 0.693 t (或 t = 1.443 T 1/2 ) ( 29-5 )
2 . RL 串联电路的暂态过程
与 RC 串联电路进行类似分析可得, RL 串联电路的时间常数 t 及半衰期 T 1/2 分别 为:
( 29-6 )
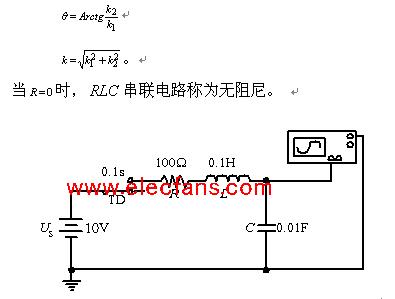
3 . RLC 串联电路的暂态过程
先讨论 RLC 电路中突然接入电源,电容器上电压满足的微分方程为
( 29-7 )
等式两边同除以 LC ,并令
( 29-8 )
则上式可化为
( 29-9 )
式( 29-9 )为一阻尼振荡方程, b 为阻尼系数, w 0 为电路的固有频率.又由本过程的两个初始条件
; ( 29-10 )
所以( 29-10 )式最终解的形式取决于 b 和 w 0 的相对大小 .
下面就分三种情况给出结果
(1)欠阻尼
当 时,称为欠阻尼,其解为
( 29-11 )
式中, ,式( 29-11 )称为阻尼振荡解.
(2)过阻尼
当 时,称为 过阻尼. 其解为:
( 29-12 )
式中:
(3)临界阻尼
当 时,称为临界阻尼,此时其解为
( 29-13 )
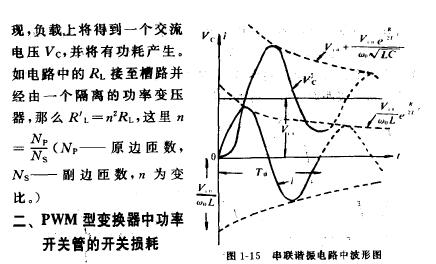
当电路达到稳定后,突然撤去电源电动势(即 E = 0 ),电路的变化类似于 充电过程 .方程的解也分为三种情况. 以上讨论的充、放电的条件是加阶越波且源内阻为零.在实验中,我们可以用源内阻很小的方波源来代替上述条件.只要方波的周期远大于电路的时间常数就可以.
上述三种情况下 U C 随时间 t 的变化如图 29-3 所示 .
【如图所示】
【设计报告要求】
1. 写明实验的目的和意义
2. 阐明实验原理和设计思路
3. 说明实验方法和测量方法的选择
4. 列出所用仪器和材料
5. 确定的实验步骤
6. 设计数据记录表格
7. 确定实验数据的处理方法
【注意事项】
1 .应用各种仪器前,仔细查阅有关说明书和使用方法.
2 .各电路元件在测量时,接地点应与仪器的接地点一致.
【思考题】
1 .在 RC 暂态过程中,固定方波的频率,而改变电阻的阻值,为什么会有不同的波形?而改变方波的频率,会得到类似的波形吗?
2 .在 RLC 暂态过程中,若方波的频率很高或很低,能观察到阻尼振荡的波形吗?如何由阻尼振荡的波形来测量 RLC 电路的时间常数?
3 .在 RC 、 RL 电路中,当 C 或 L 的损耗电阻不能忽略不计时,能否用本实验测量电路中时间常数?
 电子发烧友App
电子发烧友App



























评论