模拟滤波器实验

模拟滤波器实验

一、 实验目的

1、掌握低通滤波器的设计：

2、学会将无源低通滤波器向带通、高通滤波器的转化：

3、了解常用有源低通滤波器、高通滤波器、带阻滤波器的结构与特性：

4、了解巴特沃兹低通滤波器与切比雪夫低通滤波器的特点：

5、学会用信号源与示波器测量滤波器的频响特性：

二、 实验仪器

1、信号与系统实验箱一台。

2、40MHz示波器一台。

三、 实验原理

模拟滤波器根据其通带的特点可分为：

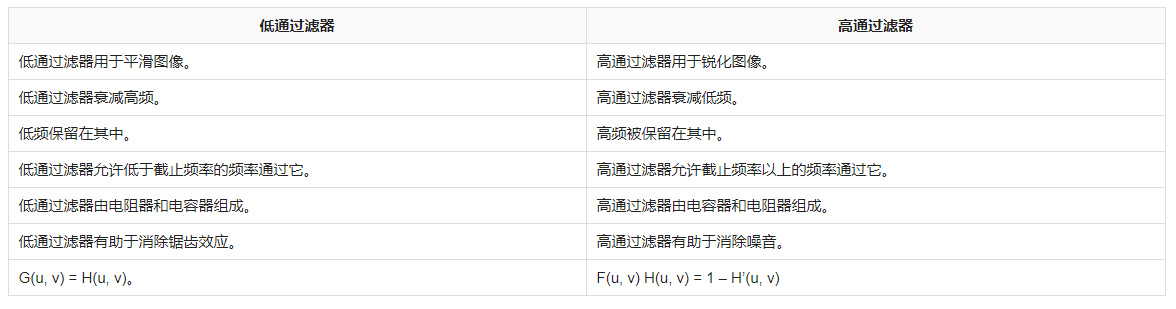
（1）    低通滤波器

（2）    高通滤波器

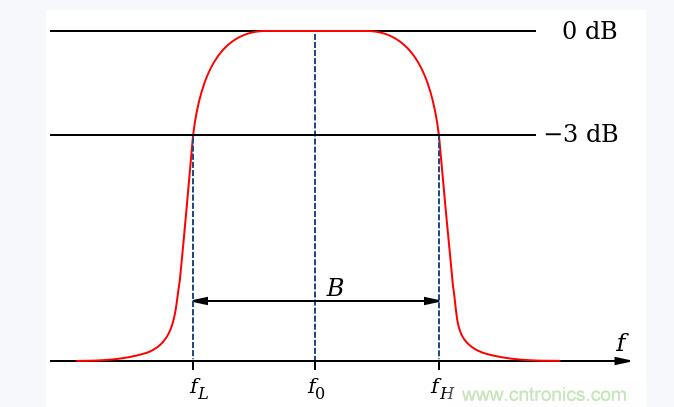
（3）    带通滤波器

（4）    带阻滤波器

在这四类滤波器中，又以低通滤波器最为典型，其他几种类型的滤波器均可以从它转化而来。

对于模拟低通滤波器的设计方法，一般是通过逼近的设计方法。在最常用的滤波器中，又以巴特沃兹滤波器、切比雪夫滤波器最为常用。

1、巴特沃兹滤波器

其频响特性为：

点：（1）最大平坦性：其滤波器在0频点处附近一段范围内是非常平直的，它是以原点最大平坦性来逼近理想低通滤波器。

（2）通带、阻带下降的单调性；

（3）具有良好的相频特性

（4）－3dB的不变性：随着N的增加，频带边缘下降越陡峭，越接近理想特性，但不管N是多少，幅频特性都通过－3dB点；

2、切比雪夫滤波器

其频响特性为：

特点：

（3）通带内波动均匀性。

（4）相位的非线性特性。

四、 实验内容及主要步骤

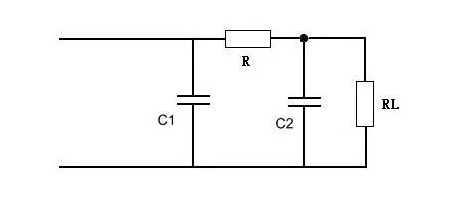
1、无源滤波器的测量：

（1）    四阶无源巴特沃斯低通滤波特性测量：

(A)－3dB频点的测量：首先函数信号发生器模块产生一1KHz的正弦信号（通过跳线K302选择“正弦波”，跳线K301选择“中”，同时可以调节W301，进行频率细调），把它接至插孔“四阶巴特沃斯无源低通”,用示波器观察“输出7”，测量四阶巴特沃斯低通滤波器在该频点的输出幅度；然后不断增加信号源的输出频率，保持其输出幅度不变，当滤波器输出信号的幅度为原来的0.707时，低频信号的频率即为该滤波器的－3dB频点。

(B) 滤波器的频响特性测量：用函数信号发生器模块产生一正弦信号，然后不断增加信号源的输出频率，并保持其输出幅度不变，测量相应频点滤波器输出信号的幅度，并记录下来。以频率与输出幅度（可换算成相对0点的相对电平值，单位为dB）为变量画出一曲线，则该曲线即为该滤波器频响特性曲线。

（2）四阶无源巴特沃斯带通滤波器特性测量

（A）   带通滤波器中心频点测量：首先用函数信号发生器模块产生一正弦信号（通过跳线K302选择“正弦波”，跳线K301选择“中”，同时可以调节W301，进行频率细调），把它接至插孔“四阶巴特沃斯无源带通”,用示波器观察“输出8”，改变信号源的输出频率，并保持其输出幅度不变，当滤波器输出信号的幅度为最大，低频信号源的频率即为该带通滤波器的中心频点。

（B）     带通滤波器的频响特性测量：用函数信号发生器模块产生一正弦信号，其频率在带通滤波器中心频点附近。然后不断增加或减少信号源的输出频率，并保持其输出幅度不变，测量相应频点滤波器输出信号的幅度，并记录下来。以频率与输出幅度（可换算成相对0点的相对电平值，单位为dB）为变量画出一曲线，则该曲线即为该滤波器频响特性曲线。

（3）    六阶无源巴特沃兹低通滤波器特性测量：

（A）－3dB频点测量：方法同四阶无源巴特沃兹低通滤波器

（B）滤波器的频响特性测量：方法同四阶无源巴特沃兹低通滤波器.

（4）六阶无源巴特沃斯高通滤波器特性测量：

（A）   －3dB频点测量：首先用函数信号发生器模块产生一正弦信号，把它接至插孔“六阶巴特沃斯无源高通”，改变信号源的频率，用示波器观察插孔“输出10”，找出六阶无源巴特沃斯高通滤波器在高端频率点的输出幅度（在该频点附近信号输出幅度保持不变），以该点输出信号幅度为参考。降低信号输出频率，当滤波器输出信号的幅度为参考输出幅度的0.707时，低频信号源的频率即为该高通滤波器的－3dB点。

（B）   滤波器的频响特性测量：用函数信号发生器模块产生一正弦信号，然后不断增加信号源的输出频率，并保持其输出幅度不变，测量相应频点滤波器输出信号的幅度，并记录下来。以频率与输出幅度（可换算成相对0点的相对电平值，单位为dB）为变量画出一曲线，则该曲线即为该滤波器频响特性曲线。

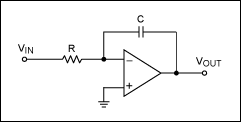
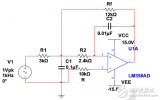
2、有源滤波器件特性测量：

（1）    二阶有源巴特沃兹低通滤波器特性测量：测量方法自拟。

（2）    二阶有源巴特沃兹高通滤波器特性测量：测量方法自拟。

（3）    二阶有源巴特沃兹带通滤波器特性测量：测量方法自拟。

（4）    二阶有源巴特沃兹带阻滤波器特性测量：测量方法自拟。

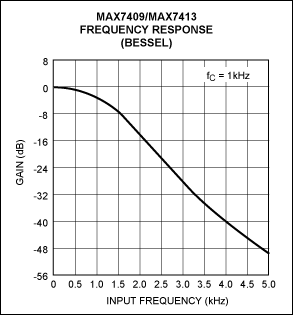
（5）    二阶有源切比雪夫低通滤波器特性测量：测量方法自拟。

（6）    八阶有源切比雪夫低通滤波器特性测量：测量方法自拟。

五、实验报告要求。

1、整理绘画出各种滤波器的滤波特性。

2、根据实验测量的数据，绘制各滤波器的幅频特性曲线。注意应将同类型的无源和有源滤波器幅频特性绘制在同一坐标上。以便比较并计算出特征频率、截止频率和通频带。

3、比较分析各种无源和有源滤波器的滤波特点。