当我说“二阶”滤波器时，我指的是使用电感 - 电容（LC）谐振或放大器的滤波器，以产生真正的二阶传递函数。
2023-09-18 15:59:24
434 
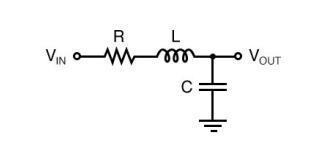
本文很好地介绍了模拟滤波器。它涵盖了基本的一阶和二阶滤波器类型以及无源和有源滤波器的优缺点。本文使用多个运算放大器实现示例推导并分析了基本的双二阶实现方案。
2023-06-10 11:52:41777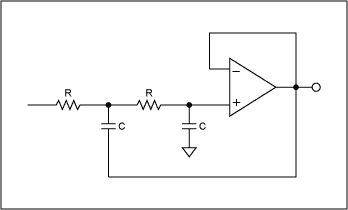 
六 调制与解调……………………………………………………….13实验七 反馈系统的自激振荡…………………………………………….17实验八 二阶网络函数的模拟…………………………………………….19实验九
2008-09-24 10:03:25
二阶有源带通滤波器原理详解
2022-11-21 11:00:492039 二阶有源高通滤波器原理详解
2022-11-18 09:48:101929 阶有源滤波器的典型结构，二阶有源低通滤波器仿真分析
2022-11-15 12:46:44930 电源调试笔记 – 二阶补偿系统仿真R2=12K 这里是笔误
2022-01-11 10:36:15
2 1引入为什么要用有源二阶滤波器？(1)从有源来说对于无源二阶低通滤波器：其幅頻方程为：我们从中可以看出其通带截止频率为有其品质因子为0.372。我们根据上图得到二阶无源低通滤波器的品质因子只有
2021-11-06 20:51:00107 本文档的主要内容详细介绍的是电路原理教程之一阶电路和二阶电路的时域分析学习课件免费下载包括了：1.动态电路的方程及其初始条件，2.一阶电路的零输入响应，3.一阶电路的零状态响应，4.一阶电路的全响应
2020-10-29 18:08:3619 1．计算一阶电路（RC、RL）满足 4 倍的时间常数略小于信号脉冲宽度的电阻值。 2．计算二阶电路的临界电阻值。三、预备知识本实验采用普通示波器来观察一阶二阶网络接通和断开直流电源的过渡过程。因为
2020-10-19 08:00:000 本文档的主要内容详细介绍的是二阶电路的复习题和答案免费下载。
2020-09-28 08:00:001 本文档的主要内容详细介绍的是网络函数的习题与详解详细说明。
2020-09-28 08:00:000 增加额外高频极点对于二阶系统的影响，如果二阶系统增加一个或者多个极点，对系统有何影响？这取决于增加的极点离谐振频率ωn的远近。
2020-04-10 11:39:377268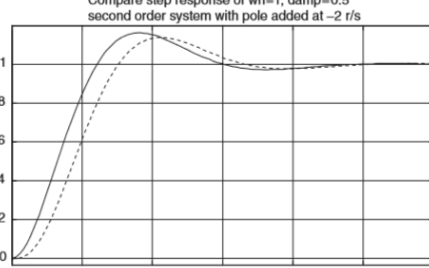 
LCR二阶振荡系统，我们假设电阻足够小，系统处于欠阻尼状态，此系统有两个复平面极点。比如，对于阻尼因子为0.2的系统，振荡的峰值约为1.6倍。
2019-12-26 15:25:021594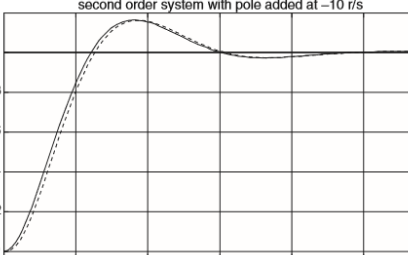 
本文档的主要内容详细介绍的是二阶电路的MATLAB资料免费下载。
2019-11-14 08:00:001 制作过程一阶HDI PCB相对简单且控制良好。由于对准，冲头和铜问题，二阶HDI PCB很复杂。
2019-08-01 16:41:3815041 本文档的主要内容详细介绍的是二阶电路的经典复习题免费下载。
2019-07-25 08:00:003 本文档的主要内容详细介绍的是RLC二阶电阻计算应用程序免费下载。
2019-04-28 16:24:3810 一阶的比较简单，流程和工艺都好控制。二阶的就开始麻烦了，一个是对位问题，一个打孔和镀铜问题。二阶的设计有多种，一种是各阶错开位置，需要连接次邻层时通过导线在中间层连通，做法相当于2个一阶HDI。第二
2018-09-15 10:51:0256392 
对于图像的边缘来说，通常会形成一个斜坡过度。一阶微分在斜坡处的值不为0，那么用其得到的边缘较粗；而二阶微分在斜坡处的值为0，但在斜坡两端值不为0，且值得符号不一样，这样二阶微分得到的是一个由0分开
2018-09-13 15:19:1427589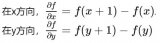 
一阶电路和二阶电路的时域分析主要内容详细包括了;动态电路的方程及其初始条件，一阶电路的零输入响应，一阶电路的零状态响应，一阶电路的全响应，二阶电路的零输入响应，二阶电路的零状态响应和全响应，一阶电路和二阶电路的阶跃响应，一阶电路和二阶电路的冲激响应，卷积积分，状态方程，动态电路时域分析中的几个问题
2018-07-25 08:00:0025 二阶滤波电路有两种结构: Sallen-key和多路反馈(KFB)
2018-06-04 09:09:1239338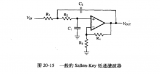 
共压力管道复杂水电系统为例，采用线弹性模型模拟水力系统，计算该水电站二阶振荡模式及非线性指标，仿真计算发现二阶振荡模式并未产生新的主导振荡模式，非线性对一阶振荡模式的幅值和阻尼影响较大。
2018-01-27 10:32:2012 在行人检测中，由于外界环境复杂变化和行人自身的不同特点，往往会造成错误检测以及遗漏检测。针对以上问题，文中提出一种基于图块和二阶统计特征的方法，提高检测的准确率。首先利用基于图块的帧差法进行前景检测
2017-11-14 10:44:5513 从滤波器阶数可分为一阶和高阶，阶数越高，幅频特性越陡峭，高阶滤波器通常可由一阶和二阶滤波器级联而成。一阶有源滤波电路的基础上再加一节RC低通滤波环节，称为二阶有源滤波电路。
2017-07-24 15:41:26198921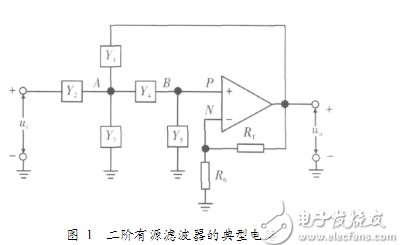 
低通滤波器是用来通过低频信号衰减或抑制高频信号，典型的二阶有源低通滤波器由两级RC滤波环节与同相比例运算电路组成，其中第一级电容C接至输出端，引入适量的正反馈，以改善幅频特性。增益为1的二阶有源低通滤波器如图所示。
2017-07-24 14:36:0028600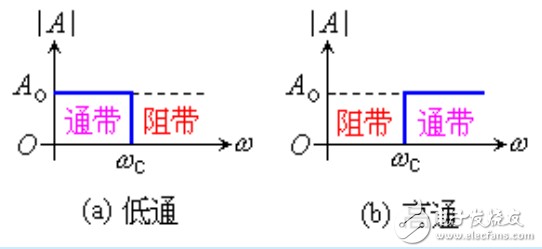 
电路设计--网络函数
2017-02-28 22:49:370 二阶高通滤波器实验数据，可绘制出相应的曲线
2016-07-04 17:57:5030 电路原理第八章 二阶电路的计算方法，零响应，全响应。大学基础课程，需要材料的挫进来。
2016-03-25 14:02:531 为了研究二阶控制系统的性能，讨论了二阶控制系统参数ζ和ωn与单位阶跃响应的关系，并介绍了基于Matlab/Simulink软件仿真环境，在单位阶跃信号作用下，利用仿真实例很好地实现了对二阶控制系统
2014-02-12 11:16:2838284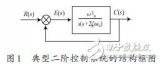 
高通滤波、二级放大、有源二阶低通滤波电路原理图如下图所示：
2012-07-23 16:54:0111960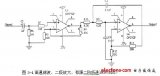 
二阶无源滤波器电路:
2012-04-19 10:43:096153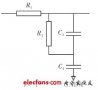 
基于探索 RLC二阶电路仿真实验技术的目的，采用Multisim仿真软件对RLC二阶电路暂态过程进行了仿真实验测试，给出了电路在过阻尼、临界阻尼、欠阻尼等情况下零输入响应及零状态响应
2012-01-10 16:30:4399 为评价控制系统的动态性能,基于二阶系统传递函数和频率特性以及时频域性能指标编程算式分析,阐述了在虚拟仪器软件平台LabVIEW 上构建二阶系统动态特性时频测试系统的设计思想,介
2011-05-28 15:28:5830 二阶全通滤波器电路函数与原理
二阶全通滤波器的传输函数的通式为
式
2010-05-23 15:30:0910253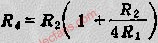 
二阶有源滤波器的传输函数
在有源滤波器的设计中，高阶滤波器的传输函数都可以分解成一阶和多个二阶传输函数的乘积。一阶传输函数比较简单，二阶函
2010-05-23 10:31:2418198 
二阶分频器低通单元电路
二阶(双元件)低通分频器电路结构如图1所示。
2009-12-21 18:48:262914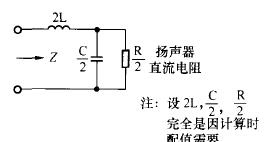 
用在系统可编程模拟器件实现双二阶型滤波器
阐述了在系统可编程模拟器件的特点以及用它设计双二阶型、连续时间低通和带通滤波器的方法。
2009-12-08 14:57:42509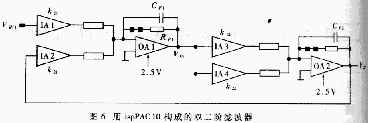 
10KHz二阶低通滤波器
2009-09-17 14:52:014856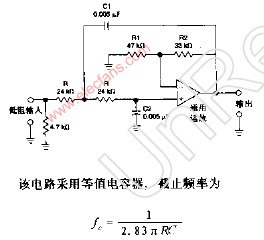 
等值元件二阶高通滤波器
2009-09-17 14:50:14664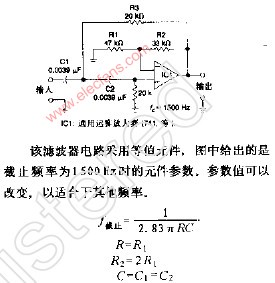 
增益为1的二阶高通滤波器
2009-09-17 14:34:282201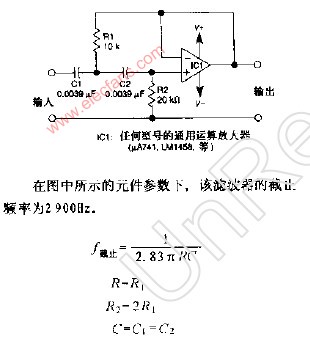 
有源话音二阶带通滤波器
该
2009-09-16 18:01:261426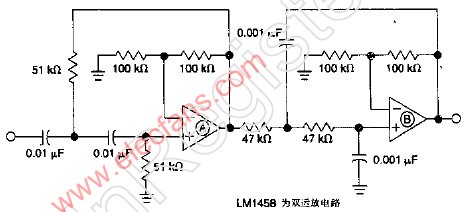 
网络函数
在图9-6-1中，表示电路中某个激励，
2009-07-27 11:49:523421 
二阶电路的零输入响应
凡用二阶微分方程描述的电路，称为二阶电路。二阶电路中含有两个独立的储能元件。本节以
2009-07-27 11:35:528642 
网络函数教案(ppt讲稿):1、网络函数及其相关的基本概念。2、网络函数的零、极点分布对时域响应和频域响应（频率特性）的影响。网络函数的零、极点分布对频域响应（频率
2009-07-08 10:23:3823 二阶高通滤波电路
2009-07-01 17:55:182261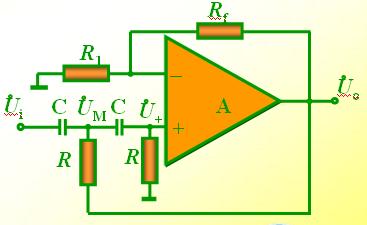 
二阶低通滤波电路
2009-07-01 17:53:431698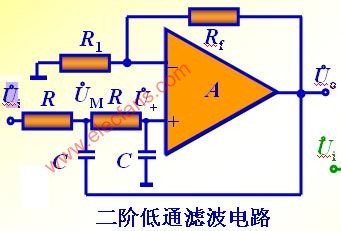 
二阶闭环系统的频率特性曲线一．实验要求1． 研究二阶闭环系统的结构参数--自然频率（无阻尼振荡角频率）ωn、阻尼比ξ对对数幅频曲线和相频曲线的影响。2． 了解和掌
2009-05-15 00:52:5555 二阶网络特性测量
一、实验目的
1、掌握二阶网络的构成方法。
2、掌握二阶网络的系
2009-05-10 00:12:074022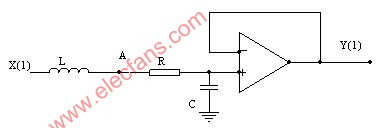 
二阶网络的零输入响应和零状态响应 一、实验目的 1．研究二阶网络的零输入响应和零状态响应的基本规律和特点； 2．了解网络参数
2009-05-10 00:08:1088 二阶RC滤波器的传递函数表
2009-05-08 08:53:5511611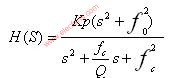 
实验目的1. 观察二阶网络在过阻尼、临界阻尼和欠阻尼三种情况下响应波形。2. 研究二阶网络参数与响应的关系。3. 进一步掌握示波器的使用。
实验原理1. 凡是
2008-12-22 11:34:01273 二阶贝塞尔滤波器
2008-12-01 13:08:046731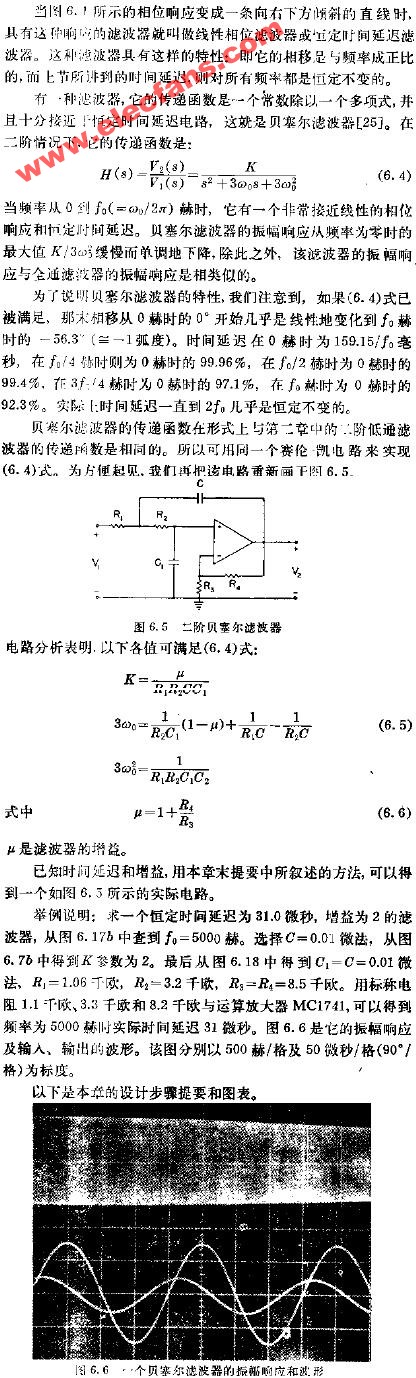 
二阶带通正反馈滤波器
2008-12-01 13:03:251718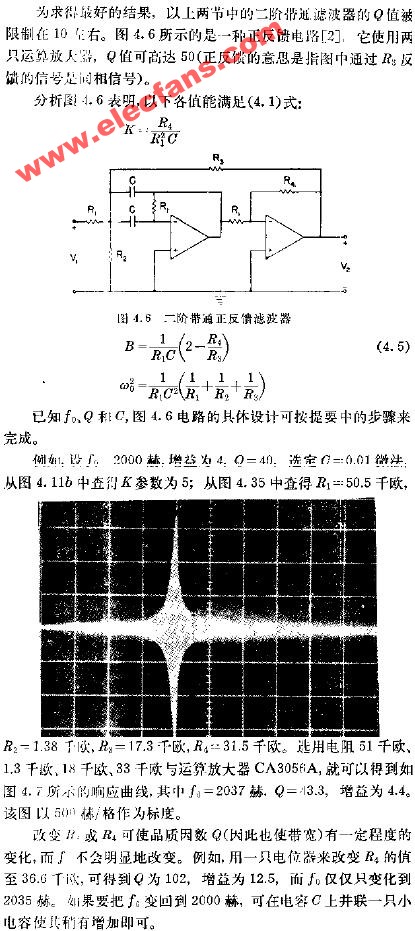 
多路反馈二阶带通滤波器
2008-12-01 13:01:142057 
二阶带通滤波器电路
2008-12-01 12:59:151148 
二阶压控电压源带通滤波电路
传递函数
2008-11-30 12:42:557839 
实验 二阶动态电路响应的研究一． 实验目的
1. 学习用实验的方法来研究二阶动态电路的
2008-11-02 22:42:0211547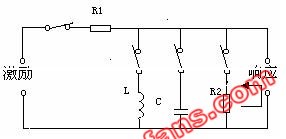 
设计二阶系统动态校正环节
一、 实验目的
1、掌握串联超前与迟后校正装置的设计方法。
2、掌握串
2008-10-16 00:36:043271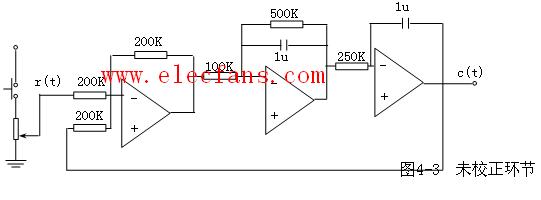 
二阶系统的时域响应
一、实验目的1.掌握用电子模拟二阶系统的实验方法2.通过实验，进一步了解二阶系统的动态性能与系统阻
2008-09-24 11:05:273153 
二阶动态电路响应的研究
一、实验目的1. 测试二阶动态电路的零状态响应和零输入响应， 了解电路元件参数对响应的影响。2.
2008-09-24 09:40:035007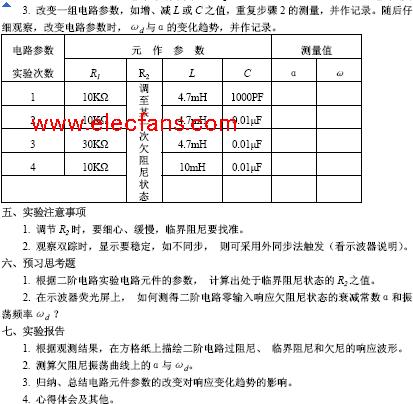 
二阶数字陷波器的设计方法及数字传输函数
下面讲解设计一个二阶数字陷波器（求数字传输函数），其模拟陷波频率为60Hz，3dB带宽为6Hz，
2008-08-01 17:24:2810289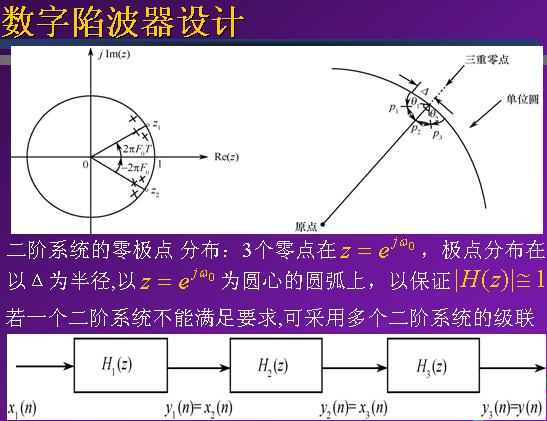 
二阶高通
2008-06-14 12:29:336102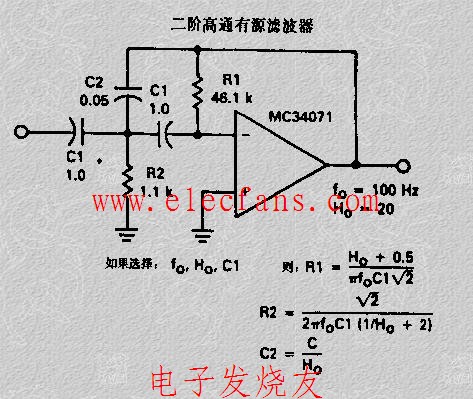 
二阶低通有源滤波器电路
2008-06-14 12:28:467245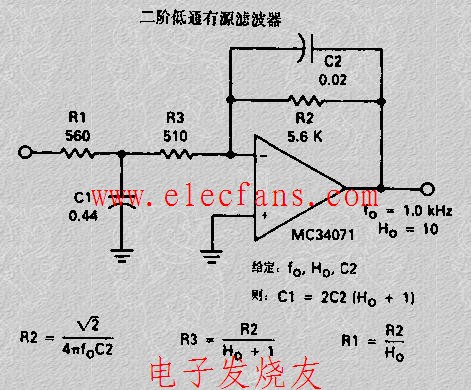 
正在加载...
电子发烧友App
工商网监
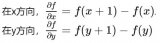
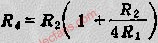
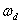
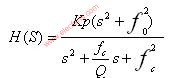
评论