微分、积分和微分方程
4.1. 知识要点和背景:微积分学基本定理
4.2 实验与观察(Ⅰ):数值微积分
4.2.1实验:积分定义、微分方程和微积分基本定理的联系
◆步骤1.
【 n=4;n1=n+1;x=linspace(0,pi,n1);f=myfun2_2(x);[0:n;x;f] 】
◆步骤2.
【 y(1)=0; y(2)=y(1)+f(1)*(x(2)-x(1));
P_intial=[x(1),y(1)],P_final=[x(2),y(2)], 】
◆步骤3.
【 y(3)=y(2)+f(2)*(x(3)-x(2));
P_intial=[x(2),y(3)], P_final=[x(3),y(3)] 】
◆ 步骤4。
【 Dy=y(3)-y(2) 】
【 DS=f(2)*(x(3)-x(2)) 】
◆步骤5 .
4.2.2 求解数值积分的Matlab积分命令
◆观察cumsum指令的功能。
【 x=[1 1 1 1 1];I=cumsum(x) 】
◆观察:用累积和命令cumsum计算积分。
【 x=linspace(0,pi,50); y=sin(x);
T=cumsum(y)*pi/(50-1);I=T(50) 】
◆观察梯形公式计算的效果。
【 x=linspace(0,pi,50); y=sin(x);T=trapz(x,y) 】
◆ 观察辛普森积分公式的计算效果。
【 I1=quad('sin',0,pi), I2=quad8('sin',0,pi), 】
◆ 观察:用解常微分方程的方法计算积分 。
【 y0=0;[x,y]=ode23('myfun2_2',[0,pi],y0);s=length(y);y(s) 】
【 y0=0;[x,y]=ode45('myfun2_2',[0,pi],y0);s=length(y);y(s) 】
4.2.3 观察程序及其说明
zxy4_1.m (观察方程的解曲线族,图4.1)
【 clf,clear,a=0;b=pi;c=0;d=2.2;n=20;
[X,Y]=meshgrid(linspace(a,b,n),linspace(c,d,n));
z=X.*Y; Fx=cos(atan(sin(X)));Fy=sin(atan(sin(X)));
quiver(X,Y,Fx,Fy,0.5),hold on,axis([a,b,c,d])
[x,y]=ode45('zxy4_1f',[0,pi],0);
[x1,y1]=ode45('zxy4_1f',[0,pi],0.2);
[x2,y2]=ode45('zxy4_1f',[0,pi],0.4);
[x3,y3]=ode45('zxy4_1f',[0,pi],0.6);
plot(x,y,'r.-',x1,y1,'r.-',x2,y2,'r.-',x3,y3,'r.-'), xlabel('x') ,ylabel('y') 】
zxy4_1f.m
【 function dy=zxy4_1f(x,y)
dy=sin(x); 】
. 观察 程序zxy4_2.m (图4.1~4.3)
【 clf, a=0;b=4*pi;n=31;
x=linspace(a,b,n); y=zeros(1,n); y(1)=0; s(1)=0; for i=1:n-1 dy=myfun2_2(x(i));
y(i+1)=y(i)+dy*(x(i+1)-x(i));
hh(i)=myfun2_2(x(i));
s(i+1)=s(i)+hh(i)*(x(i+1)-x(i));
end
a1=0.9*a;b1=1.1*b; % 设置坐标范围。
ymin=min(y');ymax=max(y'); ymin1=ymin*0.9;ymax1=ymax*1.1;
subplot(2,1,1), %在第一幅图中画垂线,和原函数。
fplot('1-cos(x)',[0,pi],'r:');axis([a1 b1 ymin1 ymax1]),hold on,
plot([x(1) x(1)],[ymin ymax]);
subplot(2,1,2), %在第二幅图中画被积函数图象。 fplot('myfun2_2',[a b],'-k');hold on,axis([a1 b1 ymin1 ymax1])
for i=1:n-1 %在第I个子区间上计算。 subplot(2,1,1),
plot([x(i+1) x(i+1)],[ymin ymax]); %在各分点画竖线。
plot([x(i) x(i+1)],[y(i),y(i)]); %画水平线。
h=plot([x(i+1) x(i+1)],[y(i),y(i+1)]); %画表示增量的垂线。
set(h,'linewidth',3,'color','b'); %设置线宽和颜色。 h1=plot([x(i) x(i+1)],[y(i) y(i+1)],'.-'); %画折线,设置图形属性 。
set(h1,'linewidth',2,'markersize',18);
subplot(2,1,2),
xx=[x(i) x(i) x(i+1) x(i+1)]; yy=[0 hh(i) hh(i) 0]; %计算矩形顶点坐标。 patch(xx,yy,[0.7 0.7 0.7]); %在第二幅图中画矩形块并填充颜色。
plot([x(i+1) x(i+1)],[ymin ymax]);
plot([x(1) x(1)],[s(i),s(i+1)],'r','linewidth',5); %在y轴上画面积增量线段。
plot(x(1),y(i+1),'r.','Markersize',18); subplot(2,1,1),plot([x(i+1) x(i+1)],[ymin ymax]);
h=plot([x(1) x(1)],[s(i),s(i+1)]); %画相应的辅助线段。
set(h,'linestyle','-','linewidth',5,'color','red');
plot(x(1),y(i+1),'r.','Markersize',18);
plot([x(1) x(i+1)],[s(i+1) y(i+1)],'r--')
pause %暂停,n大时应该去掉。
end 】
myfun2_2.m (选择其它的函数进行实验,可修改此程序)
【 function y=myfun2_2(x) sin(x); %y=sin(x)./(x); 】
4.3 实验与观察(Ⅱ): Matlab符号微积分简介
4.3.1 创建符号变量
4.3.2 求符号极限limit指令
◆观察 :求下列问题的极限:
【 syms x a
I1=limit('(sin(x)-sin(3*x))/sin(x)',x,0)
I2=limit('(tan(x)-tan(a))/(x-a)',x,a)
I3=limit('(3*x-5)/(x^3*sin(1/x^2))',x,inf) 】
4.3.3 求导指令diff
1.符号求导指令diff
◆
【 syms x y
f=sym('exp(-2*x)*cos(3*x^(1/2))')
diff(f,x)
g=sym('g(x,y)') %建立抽象函数。
f=sym('f(x,y,g(x,y))') %建立复合抽象函数。
diff(f,x)
diff(f,x,2) 】
2.数值求导指令diff
【 x=linspace(0,2*pi,50);y=sin(x);dydx=diff(y)./diff(x);
plot(x(1:49),dydx),grid 】
4.3.4 求符号积分int
【 syms x y z
I1=int(sin(x*y+z),z)
I2=int(1/(3+2*x+x^2),x,0,1)
I3=int(1/(3+2*x+x^2),x,-inf,inf) 】
4.3.5 化简、提取和代入
【 syms x a
t=(a+x)^6-(a-x)^6
t_expand=expand(t)
t_factor=factor(t_expand)
t_simplify=simplify(t) 】
◆ 观察: 将 代入表达式 中求值。
【 syms a b c x y a0 y0
f=a*b+c/x*y;
a='a0';b=1;c=4;x='x0';y=5;
t= subs(f) 】
【 syms a b c x y a0 y0
f=a*b+c/x*y;
subs(f,{a,b,c,x,y},{'a0',1,4,'x0',5}) 】
4.4应用、思考和练习
4.4.1 追击问题
1.追击问题的数值模拟
2. 追踪雷达失效的情形
3. 追线问题的解析解
【 syms y a v s0
x=sym('x(y)'); t=sym('t(y)'); %定义函数关系。
f_left=-y*diff(x,y); f_right=s0+a*t-x; %方程左、右边表达式。
r_left=diff(f_left,y), r_right=diff(f_right,y) %求导 】
【 syms y d r
xs=simplify(dsolve('D2x=-r*sqrt(1+Dx^2)/y','x(20)=0','Dx(20)=0','y')) 】
【 r=0.4; y=20:-0.01:0;
x=1/2*(y.^(1+r)*r*20^(-r)+y.^(1-r)*r*20^r-40*r-y.^(1+r)*20^(-r)+y.^(1-r)*20^r)/(-1+r^2);
shg,comet(x,y) 】
4.4.2 应用问题
1.枪支的设计
【clear,clf
x=[0.0127,0.0254,0.0381,0.0508,0.0635,0.0762,
0.0889,0.1016,0.1143,0.1270,0.1397,0.1524,0.3175,0.3302,0.3429,0.3556,
0.3683,0.3810,0.3937,0.4064,0.4191,0.4318,0.4445,0.4572,0.1651,0.1778,
0.1905,0.2032,0.2159,0.2286,0.2413,0.2540,0.2667,0.2794,0.2921,0.3048,
0.4699,0.4826,0.4953,0.5080,0.5207,0.5334,0.5461,0.5588,0.5715,0.5842,
0.5969,0.6096];
p=[0.10135,0.20064,0.27303,0.31095,0.33094,0.33991,0.34474,0.33577,
0.31508,0.29578,0.27717,0.26131,0.11859,
0.11238,0.10687,0.10204,0.09215,0.09308,0.08894,
0.08480,0.08067,0.07722,0.07377,0.07032,0.24545,
0.23097,0.21718,0.20339,0.19167,0.17995,0.16823,0.15789,
0.14824,0.13927,0.13238,0.12548,0.06757,0.06481,0.06205,0.05929,
0.05654,0.05378,0.05102,0.04826,0.04550,0.04274,0.04067,0.03861];
[xx,k]=sort(x);
pp=p(k);plot([0,xx],[0,pp],'-'),grid on,
xlabel('枪 管 长 度 x'),
ylabel('压 强 p') 】
2.天然气井的开采量
 电子发烧友App
电子发烧友App










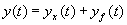











评论