摘要
本文基于LM3445的传统非隔离式解决方案,详细说明其工作原理。我们将对这种线性稳压公式进行推导和分析。通过实际实验结果对计算结果进行验证,并证明其能够非常紧密地匹配。为了评估大批量生产的可行性,我们对输出电流容限进行了彻底的研究和分析。结果证明,传统解决方案难以达到全部批量生产电流容限,特别是在当前市场所要求的更高输出应用的发展趋势下更是如此。
为了解决这个问题,我们建议使用一个简易线性稳压补偿电路。我们从理论计算和实验测量结果两个方面,对这种建议解决方案进行了验证。根据推导的输出电流和线性稳压速率公式,对实际批量生产所要求的最终总电流容限进行分析。根据所得结果,我们发现,在达到这种实际要求方面,实现了巨大的进步。最后,基于样机对测试结果和计算结果进行比较;经证明,它们非常匹配。
1、 引言
随着LED室内照明的日益增长,非隔离式方案和隔离式方案都变得越来越流行。特别是,高线性稳压的高PF和精确恒定电流模式方案成为市场的主导方案。但是,由于输出电压变得更高更宽,传统LM3444/L3445非隔离式应用无法达到这种宽余量要求,从而进一步限制了LM3445/LM3445的应用。
鉴于上述问题,本文的主要目标在于精确线性稳压要求的高输出应用。在本文中,通过第2章的一些公式,阐述一般工作原理。利用这些公式,我们可以求解最终输出电流。为了对结果进行评估,第3章介绍了一个统一公式,通过它输出电流得到简化。另外,第3章还进一步详细说明了电流容限分析。第4章给出了一些基于样机的设计例子。文章给出了计算结果和仿真结果,并把它们与实验结果进行比较。经证明,它们的匹配非常好。但是,深入研究后,我们发现仍然很难达到批量生产的电流容限要求。
为了解决这个问题,我们在第5章提出了一个建议补偿电路。通过计算和仿真实验,对这个补偿电路进行了验证。最终,实验证明,该电路明显改善了线性稳压和电流容限性能。利用这种电路,得到改进的线性稳压将在实际应用具备更强的竞争力,特别是在LED R30/PAR30/A19/E27 LED照明应用中。
2、 传统非隔离式LM3444/LM3445解决方案的原理
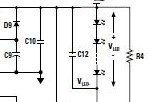
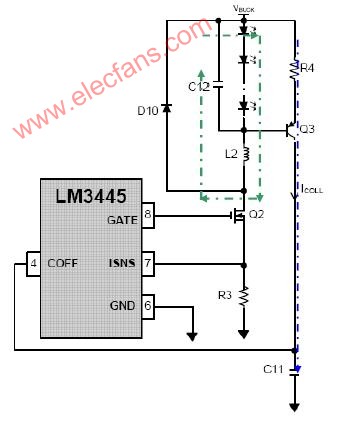
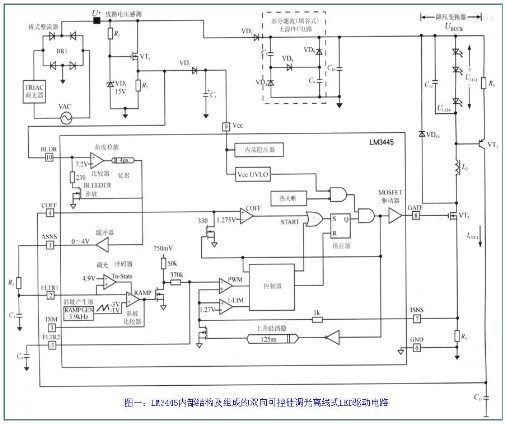
图1显示了更高PF的传统非隔离式解决方案。为了方便讲解其工作原理,我们给参数做如下定义:
•Vout:LED输出电压
•I:单时间段内等效时间值
•Kfeed:输入AC电压的前馈系数
•Rup:toff充电电阻器
•Cchar:toff充电电容器
•Vinmin:AC输入电压最小值
•Vinmax:AC输入电压最大值
•Vinac:AC输入电压
•_noimp:无改进线性稳压电路函数
•_imp:改进线性稳压电路函数

图1 高PF的传统建议非隔离式解决方案
这是一种典型的无反馈环路应用,但是它具有下列特性:
1、更高的PF。通过输入前馈电路实现。
2、恒定电流。这是通过LED输出电压检测toff电路实现。
AC输入电压可表示如下:

如图1所示,C1大于C2,目的是实现更高的PF值,例如:C1/C2 = 220n/10n。LM3444或者LM3445的针脚5的电压可以表示为:

toff的充电电流为:

进行实际计算时,Veb_Q1可选择0.6作为参考设计。
因此,toff可写为:

频率可以表示为:

电感器的纹波电流为:

因此,最大电流和平均电感电流公式可写为:

那么,LED输出电流为:

3、 基于传统解决方案的LED电流线性稳压分析
由于LED电流已在上面做了推导,因此我们可以把总公式写为:


为了推导每个输入电压的LED电流变化,可对公式(10)进行简化,因为Vout一般小于Vinac,并且Vout大于Vbe_Q2。公式可简化为:

那么,整个输入范围内的LED电流变化可利用公式(11)推导出。

我们可以看到,LED电流变化严重依赖于Vout,其意味着当LED电压较低时它可以使用更高的线性稳压,在这种情况下,其非常适合于GU10应用。
3.1 批量生产期间Δ LED电流变化分析
公式(11)推导出LED电流变化,但是这种变化在整个输入范围受Rs、L、Cchar和Rup容限的影响。根据批量生产要求,我们对其进行如下分析:
1、批量生产时Δ LED电流变化受Rs(例如:2%容限)影响如下:

2、批量生产时Δ LED电流变化受Rup(例如:2%容限)影响如下:

3、批量生产时Δ LED电流变化受Cchar(例如:10%容限)影响如下:

4、批量生产时Δ LED电流变化受L(例如:16%容限)影响如下:

5、批量生产时某个Vled下的Δ LED电流变化极端情况如下:

正常情况下,相比LED电流变化,这种总变化非常小。
3.2 批量生产期间的LED电流容限分析
在批量生产中,LED电流受到规定。正常情况下,要求它在±5%范围内,其在整个输入范围与Vled、kfeed、L、Cchar和Rup的容限无关。
由公式(9),我们知道,LED电流变化受到这些参数的影响。下面是详细分析。
1、批量生产时LED电流变化受Rs(例如:2%容限)影响情况如下:

2、批量生产时LED电流变化受Rup(例如:2%容限)影响情况如下:

3、批量生产时LED电流变化受Cchar(例如:10%容限)影响情况如下:

4、批量生产时总LED电流变化受L(例如:16%容限)影响情况如下:

5、批量生产时总LED电流变化受kfeed(例如:2%容限)影响情况如下:

6、批量生产时某个Vled下的极端LED电流变化如下:

那么,按照批量生产要求总LED电流容限可表示为:

4 基于传统解决方案的线性稳压与批量生产电流容限设计举例证明
为了验证上面推导计算结果的有效性,我们按照表1所列参数制作一个样机。

表1 样机参数
利用第2章的公式(5),得到图2所示频率曲线图:

图2 小于90Vac和140Vac的无改进解决方案频率
利用第2章的公式(7)和(8),得到电感器的最大电流和平均电流(参见图3):

图3 小于90Vac和140Vac的无改进解决方案输出电流
图4和图5显示了小于90Vac和140Vac的仿真和实验结果。

图4 90Vac以下电感电流和输出电流的仿真结果

图5 90Vac以下电感电流和输出电流的测试结果
测量和仿真得电流波形(参见图4和图5)几乎完全一样;输出纹波表明存在一些小的差异,原因是LED仿真模型和实际测试LED负载之间有差异。

图6 140Vac以下电感电流和输出电流的仿真结果

图7 140Vac以下电感电流和输出电流的测试结果
从图6和图7所示结果来看,计算结果好像密切匹配仿真结果与实际测量结果。这个结果为后面的容限分析提供了有力的理论支撑。
利用第2章的公式9,计算出标准输出电流;得到批量生产期间考虑到参数容限情况下的最大和最小输出电流:


图8 90Vac和140 Vac以下无改进解决方案的输出电流
利用3.2小节的公式(23),得到批量生产期间考虑到参数容限情况下的极端LED电流变化。

图9 90Vac到140Vac以下无改进解决方案组件容限对LED输出电流变化的影响情况
利用3.2小节的公式(24),得到批量生产期间的总LED电流容限(参见图10):

图10 批量生产时90Vac到140Vac以下无改进解决方案的总LED电流容限
从公式(24),我们可以看到,90Vac到140Vac以上的正常LED电流变化为17mA,线性稳压为± 3.3%,这对单个组件而言是可以接受的。但是,实际工程的主要问题是总调节可行性,也即考虑组件容限情况下的总LED电流容限。由图8,我们知道,受组件容限影响的输出电流变化约为32mA。因此,批量生产时的总LED电流容限为± 8%以上,如图10所示。在实际生产过程中,这同样很难实现。从上述分析我们可以知道,线性稳压是改善输入范围总容限的关键。
5 改进型非隔离式LM3444/LM3445解决方案工作原理
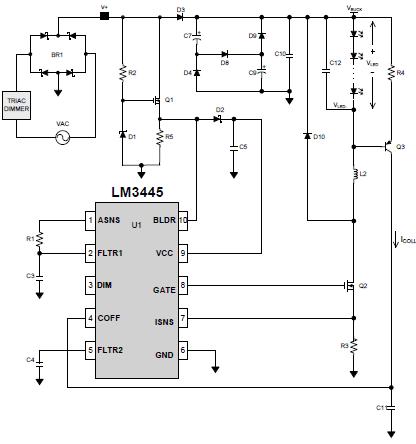
为了改善线性稳压,我们建议使用图11所示线压补偿。

图11 改进型线压补偿电路
为了降低图11所示电路的闩锁电流容限,可使用更高精度的电阻器R21、R23和R1_comp。为了减少D11、Q3和Q4的正向电压影响,我们建议C7电压稍高一些(例如:20Vdc)。为了知道不同温度下的电流容限,规定V_C7为20V,Q4的V_c为20V,而R_comp为300K,然后进行SPICE温度扫描仿真。结果如图12所示。

图12 0°C、25 °C、50 °C和85 °C以下温度扫描仿真结果
由该结果,我们知道温度容限为±3%,因此可以进入实际设计。
在安装补偿电路(参见图11)以后,经过改善的toff的充电电流为:

为了减少Q3和Q4的Vbe的影响(如图11所示),我们建议,公式(27)的系数k尽可能地大,这样我们便可在设计中忽略Vbe。
最大电流和平均电感电流公式与第2章中的公式(7)和公式(8)一样。最终LED电流公式如下:
如果不考虑其他组件容限,则输出LED电流的标准化公式可以写为:

在实际计算过程中,我们可以做如下规定:0.95Char、0.99Rs、0.99Rup、1.08L和0.99 kfeed,以便得到最大LED输出电流。该计算公式如下:

利用相同的分析,我们可以做如下规定:1.05 Char、1.01Rs、1.01 Rup、0.92 L和1.01 kfeed,以便得到最小LED输出电流。该计算公式如下:

那么,我们可以得到下列频率范围和电感电流波形相关计算方法。

图13 90Vac和140Vac以下频率

图14 90Vac和140Vac以下电感电流
图15和图16显示了90Vac和140Vac以下实验结果

图15 90Vac以下电感电流和输出电流测试结果

图16 140Vac以下电感电流和输出电流测试结果
图17显示了线性稳压计算结果:

图17 线性稳压计算改善至±1%以下
输出电流为一条输入电压的非线性曲线,而非线性曲线。补偿参数极大影响这条曲线。在实际设计中,工程师可以通过调整线压补偿参数来对这条曲线进行优化。
为了验证该结果,使用图18所示测量结果与计算结果比较。

图18 极端电流容限计算改善至±6.6%
由图18,我们可以知道,由于使用了改进线性稳压电路,极端电流容限也得到了改善。为了达到这种非常严苛的极端电流容限,我们的解决方案必须进一步改进,以适应一些特殊用户的要求。
如果考虑90Vac以下的电流容限,则可得到:

如果90Vac以上的容限基本相同则可以达到这个目标;因此,图19给出了一种备选建议方法。

图19 120Vac到140Vac以下线性稳压改善电路
LM3445/LM3444的针脚5电压计算方法如图20和图21所示:

图20 添加图20电路时的LM3445/LM3444针脚5电压

图21 使用图19电路后线性稳压得到较大改善
通过前面的分析,我们可以得出结论:这种电路可帮助改善线性稳压。但是,如果使用线压补偿电路的电流容限可达到批量生产要求,则不能使用这种附加二极管电路。但是,如果PCB布局有多余空间,则TI仍然推荐在实际设计中使用这种附加二极管电路。
最后,图22显示了备选方法的完整改善解决方案。

图22 大幅改善线性稳压的备选方法完整解决方案
结论
本文基于传统非隔离式LM3444/LM3445,彻底分析了输出电流线性稳压和电流容限。结果是线性稳压并不理想。为了解决这个问题,我们提出了一种改进解决方案。另外,我们还阐述了线性稳压和总电流容限。我们通过理论分析和实际实验,证明了这种解决方案的可行性。
 电子发烧友App
电子发烧友App










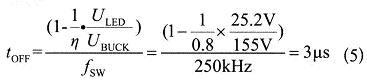











评论