MPU-6000(6050)为全球首例整合性6轴运动处理组件,相较于多组件方案,免除了组合陀螺仪与加速器时间轴之差的问题,减少了大量的封装空间。运动感测游戏 现实增强 电子稳像 (EIS: Electronic Image Stabilization) 光学稳像(OIS: Optical Image Stabilization) 行人导航器 “零触控”手势用户接口 姿势快捷方式 认证
MPU6050互补滤波法融合四元数姿态原理及代码
小四轴的飞行,姿态检测主要用到的传感器是MPU6050。从MPU6050读出来的加速度和角速度数据最后要转成姿态,可以转换成欧拉角(偏航角、俯仰角和滚转角)或四元数表示,为了减少计算量(欧拉角涉及正弦运算,运算量相对较大),方便在STM32主控上实现,可以转换成四元数表示。
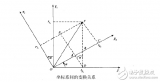
那么问题来了,四元数姿态融合算法哪家强?这里介绍圆点博士小四轴飞控开源代码关于四元数姿态融合的算法以及代码实现,不能说最强(国外有很多优秀的飞控算法),只是实现效果可以满足小四轴的成功飞行,个人水平渣渣,请大牛批评指正。博士的代码中主要用到的是互补滤波法。下图为该方法的原理图(来自论文:禤永俊,《《四轴飞行器遥感平台的实现方案》》)。
先介绍一下互补滤波的基本概念,这是阿莫论坛上一个会员的总结:对mpu6050来说,加速度计对四轴或小车的加速度比较敏感,取瞬时值计算倾角误差比较大;而陀螺仪积分得到的角度不受小车加速度的影响,但是随着时间的增加积分漂移和温度漂移带来的误差比较大。所以这两个传感器正好可以弥补相互的缺点。
不过要怎么弥补呢?经过上面的介绍是否感觉到可以用滤波器做文章呢?这里讲的互补滤波就是在短时间内采用陀螺仪得到的角度做为最优,定时对加速度采样来的角度进行取平均值来校正陀螺仪的得到的角度。就是,短时间内用陀螺仪比较准确,以它为主;长时间用加速度计比较准确,这时候加大它的比重,这就是互补了,不过滤波在哪里?加速度计要滤掉高频信号,陀螺仪要滤掉低频信号,互补滤波器就是根据传感器特性不同。
通过不同的滤波器(高通或低通,互补的),然后再相加得到整个频带的信号,例如,加速度计测倾角,其动态响应较慢,在高频时信号不可用,所以可通过低通抑制高频;陀螺响应快,积分后可测倾角,不过由于零漂等,在低频段信号不好。通过高通滤波可抑制低频噪声。将两者结合,就将陀螺和加表的优点融合起来,得到在高频和低频都较好的信号,互补滤波需要选择切换的频率点,即高通和低通的频率。
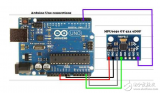
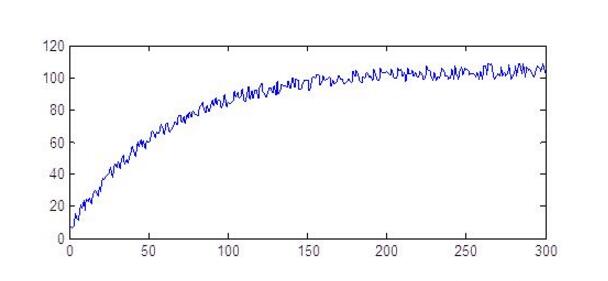
我个人觉得互补滤波在博士代码里的基本思想是以角速度积分得到角度为主进行姿态解算,但是由于周围环境或自身器件的原因,角速度计积分出来的角度可能会产生误差的累积,长时间可能引起严重的角度偏移,而加速度计虽然精度不高但没有积累误差,可以用来对角度进行纠正。通过上位机采集互补滤波法融合的四元数姿态数据并显示如下图,实验证明,这种算法很好的消除了角度偏移。
下面来讨论加速度计测出来的加速度向量如何纠正角度:
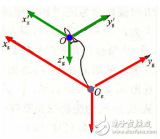
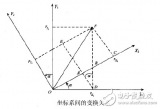
(1)首先是要用上一次融合的四元数估测出机坐标系下的重力加速度向量,地理坐标系下的重力加速度向量是r(E)=[0 0 1],这里要将地理坐标系下的重力加速度转换成机坐标系下的重力加速度,如下(具体参考:秦永元,《惯性导航-第二版》,P251)
r(E)=C(E-》A)r(A) //E(earth)表示r(E)是地理坐标系下的重力加速度向量,C(E-》A)表示从地理坐标系(E:earth)转换成机(A:airplane)坐标系的转换四元数矩阵
r(A)=R(-1)(C(E-》A))r(E) //R(-1)(C(E-》A))表示对矩阵C(E-》A)取逆
r(A)为估测出的机坐标系下的重力加速度向量,因为这是从上一次的姿态四元数中导出的向量,而姿态四元数主要是角速度计读取的值的换算,所以这里只能说估测。
(2)然后我们要得到加速度计的重力加速度值,因为加速度计是固联在机体上的,所以读出来的向量是机坐标系下的加速度向量,又因为小四轴运动速度较慢,除开重力以外的加速度值一般较小,在误差允许范围内我们可以假定加速度计测出来的就是重力加速度向量。
(3)将机坐标系下的估测的重力加速度向量和加速度计测出的重力加速度向量分别规范化为a,b,然后叉积,叉积的结果为c=|a||b|sin(A)r(D),sin(A)角度偏移的正弦,r(D)为方向,小角情况下认为sin(A)=A,A为偏移的角度,而且|a|=|b|=1,故叉积后角度偏移算出来了。
(4)将角度偏移乘以一定的系数叠加在角速度积分结果上,为什么要乘以一定的系数?这是因为这里算出的角度偏移是以加速度计为基准的,而加速度计的误差较大,直接叠加可能会引起比较大的震荡,所以要乘以一定的系数FACTOR,但FACTOR不能太小,否则纠偏效果不好,具体取值可以试凑,然后在上位机观测结果。
角度增量出来后接下来就好办了,主要是将各种计算结果往四元数微分方程一代,结果就出来了,简单推导如下(具体见秦永元,《惯性导航-第二版》,p254)
d(Q)/d(t)=1/2 × Q叉乘w(A) Q为上一次的姿态四元数,w(A)表示MPU6050读出的机体坐标系下的角速度
delta(Q)=1/2 × Q叉乘(w(A) ×delta(t)+c) delta(t)为积分时间
Q(new)=Q+delta(Q) 新的四元数姿态求出
以下是代码实现,attitude是上一次姿态融合的四元数(内存地址),gyr[3]是MPU6050读出来的角速度,acc[3]是MPU6050读出来的加速度,interval为积分时间。
void mix_gyrAcc_crossMethod(quaternion * attitude,const float gyr[3],const float acc[3],float interval)
{
const static float FACTOR = 0.001;//取接近0的数
//
float w_q = attitude-》w;
float x_q = attitude-》x;
float y_q = attitude-》y;
float z_q = attitude-》z;
float x_q_2 = x_q * 2;
float y_q_2 = y_q * 2;
float z_q_2 = z_q * 2;
//
// 加速度计的读数,单位化。
float a_rsqrt = math_rsqrt(acc[0]*acc[0]+acc[1]*acc[1]+acc[2]*acc[2]);
float x_aa = acc[0] * a_rsqrt;
float y_aa = acc[1] * a_rsqrt;
float z_aa = acc[2] * a_rsqrt; //加速度计测量出的加速度向量(载体坐标系下)
//
// 载体坐标下的重力加速度向量,单位化。
float x_ac = x_q*z_q_2 - w_q*y_q_2;
float y_ac = y_q*z_q_2 + w_q*x_q_2; //通过四元数旋转矩阵与地理坐标系下的重力加速度向量[0 0 0 1]叉乘得到载体坐标系下的重力加速度向量
float z_ac = 1 - x_q*x_q_2 - y_q*y_q_2;//(主要)角速度计测出的四元数表示的载体坐标系下的重力加速度向量(这里已转换成载体坐标系下)
//
// 测量值与常量的叉积。
float x_ca = y_aa * z_ac - z_aa * y_ac;
float y_ca = z_aa * x_ac - x_aa * z_ac;
float z_ca = x_aa * y_ac - y_aa * x_ac;//角速度计测出的角度误差,叠加的FACTOR大小可以实验试凑
//
// 构造增量旋转。
float delta_x = gyr[0] * interval / 2 + x_ca * FACTOR;
float delta_y = gyr[1] * interval / 2 + y_ca * FACTOR;
float delta_z = gyr[2] * interval / 2 + z_ca * FACTOR;
//
// 融合,四元数乘法。
attitude-》w = w_q - x_q*delta_x - y_q*delta_y - z_q*delta_z;
attitude-》x = w_q*delta_x + x_q + y_q*delta_z - z_q*delta_y;
attitude-》y = w_q*delta_y - x_q*delta_z + y_q + z_q*delta_x;
attitude-》z = w_q*delta_z + x_q*delta_y - y_q*delta_x + z_q;
quaternion_normalize(attitude);//归一化
}
 电子发烧友App
电子发烧友App





















评论