《自动化学报》：基于小样本学习的图像分类技术综述

基于小样本学习的图像分类技术综述

人工智能技术与咨询 昨天

本文来自《自动化学报》，作者李颖等

图像分类是一个经典的研究课题, 典型的图像分类算法涉及两个问题, 一是如何对图像特征进行更好的表示, 二是如何学习好的分类参数. 随着卷积神经网络(Convolutional neural networks, CNN)的设计越来越深层化, 图像特征的表示能力越来越强, 同时也能对图像进行自动分类. 在CNN提出之前, 人类通过人工设计的图像描述符对图像特征进行提取, 效果卓有成效, 例如尺度不变特征变换(Scale-invariant feature transform, SIFT)[1]、方向梯度直方图(Histogram of oriented gradient, HOG)[2], 还有词袋模型(Bag-of-words, BoW)[3-6]等, 但是人工设计特征通常需要花费很大精力, 并且不具有普适性. 基于CNN的深度学习在2012年的ILSVRC挑战赛上取得了巨大成功, 同时由于大数据、计算硬件的发展以及反向传播算法[7]的提出, 深度学习在图像分类领域[8]表现出优异性能.

深度学习的优势有赖于大数据, 在大数据的驱动下, 机器能够进行有效学习, 然而数据量不足会导致模型出现过拟合等问题, 虽然简单的数据增强(Data augmentation, DA)和正则化技术可以缓解该问题, 但是该问题并没有得到完全解决[9], 故针对小数据集的小样本学习成为了解决这类问题的关键技术. 2003年Li等首次提出了One-shot learning问题并利用贝叶斯框架[10-11]对视觉对象进行学习, 与之相比, 深度学习技术在小样本图像分类任务上具有更大的潜力. 小样本学习的产生有两个因素, 一是训练数据量少. 比如在医疗领域, 医学影像的产生来源于病例, 通常少量的病例并不能够辅助机器对医疗影像进行分析. 二是让机器学会以人类的方式进行学习, 即类人学习. 人类能够在获取少量样本的情况下, 对样本进行分类和识别, 并且具有快速理解新概念并将其泛化的能力[12], 小样本学习的目的之一就是让机器以人类的学习方式完成任务. 小样本学习目前在目标识别[13]、图像分割[14]、图像分类与检索[15]等多种图像处理任务中都有应用, 文献[16-19]从样本数量、带标签样本的数量、先验知识的作用等不同角度对小样本学习技术进行了分类讨论和分析.

在2010至2015年间, 大量的文献利用语义迁移来解决训练样本不足的问题. 例如, Mensink等[20-21]借鉴了聚类和度量学习的方法对ImageNet数据集进行分类, 并且探索了KNN (K-nearest neighbor)和NCM (Nearest class mean)分类器, 通过对每个类的语义描述, 学习一个度量, 使其在训练和测试类别间共享, 达到迁移效果; 文献[22]将语义知识迁移扩展到直推式学习, 利用已知类别推测未知类别的表示, 计算未知类别的样本相似性, 在构建数据空间分布关系时, 将数据投影到低维的语义空间, 再进一步寻找数据的空间分布, 并在AwA (Animals with attributes)[23]、ImageNet[24]以及MPII composites activities[25]数据集上取得很好的分类效果; 文献[26]提出直推式多视图嵌入框架来解决领域漂移问题, 利用异构多视图标签传播来解决原型稀疏性问题, 有效利用了不同语义表示提供的互补信息, 并在AwA、CUB (Caltech-UCSD-Birds)[27]、USAA (Unstructured social activity attribute)[28]数据集上取得了很好效果; Fu等[28]为解决带有稀疏和不完整标签的社交媒体数据的属性学习问题, 利用零样本学习思想提出了一种学习半潜在属性空间的模型, 它能够表达用户自定义和潜在的属性信息, 在USAA数据集上取得很好的效果. 这些文章针对的多是零样本学习问题, 本文主要介绍小样本下的图像分类算法, 因此综述算法更集中于Few-shot learning.

近年来现有文献中基于小样本学习的图像分类算法都是采用深度学习. 将深度学习中的技术用于小样本学习中, 比如使用数据增强技术来增加样本的数量, 通过注意力机制和记忆力机制来对图像特征进行提取, 设计提取特征网络和分类器之间的映射关系, 与此同时, 迁移学习、元学习、对偶学习、贝叶斯学习以及图神经网络方法也被用于小样本图像分类的任务. 本文的小样本学习算法与其他几篇小样本文献相比较有两点区别, 一是本文阐述的小样本学习算法是针对图像分类任务, 文献[16-19]中的小样本学习算法不仅应用于图像分类, 还有识别、分割等图像任务以及小样本学习在语音、视频中的算法应用, 本文集中地对小样本图像分类算法进行了分类并归纳总结; 二是本文探索了不同的网络建模方式, 将小样本图像分类算法分为卷积神经网络模型和图神经网络模型两大类, 卷积神经网络模型主要基于CNN对图像数据建模, 图神经网络模型进一步将CNN应用在图神经网络上, 通过图结构中的节点和边来对图像数据建模.

本文的结构如下, 第1节介绍了小样本图像分类的流程, 小样本图像分类数据集和实验评价指标; 第2节将现有小样本图像分类算法按照数据结构类型分为卷积神经网络模型和图神经网络模型两大类并进行详细介绍; 第3节通过实验数据对比分析了各种算法的性能; 第4节总结了小样本图像分类面临的技术挑战并讨论了未来研究趋势; 第5节总结全文.

1.   小样本图像分类介绍

1.1   基于小样本学习的图像分类算法

小样本学习是指训练类别样本较少的情况下, 进行相关的学习任务, 一般地, 我们也希望机器通过学习大量的基类(Base class)后, 仅仅需要少量样本就能快速学习到新类(New class). 通常情况下, 小样本学习能够利用类别中的少量样本, 即一个或者几个样本进行学习. 类别下的训练样本只有一个的情况下, 小样本学习被称为One-shot learning[10], 类别下的训练样本有多个的情况下, 称为Few-shot learning[29-30], Few-shot learning包含有One-shot learning的情况.

小样本图像分类流程如图1所示, 包括准备数据集、构建用于图像特征提取的网络和设计分类器三个步骤. 以下对建立小样本图像分类流程的三个步骤进行具体介绍.

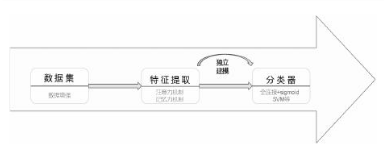
图 1  小样本图像分类流程

Fig. 1  The procedure of small sample image classification

1.1.1   数据集处理

本文将处理小样本图像数据集的方式分为两种. 一是进行数据增强, 将数据集进行量级扩增和模式扩增, 量级扩增是指针对数据量级的扩大, 模式扩增是指在量级扩增的同时, 让不同的样本包含更多的语义特性. 训练模型时, 如果每类包含大量的样本, 且这些样本包含大量的模式, 则在缓解过拟合问题的同时, 模型会具有更好的鲁棒性和泛化能力. 除了图像样本数目的扩增, 图像特征的增强也是一种数据增强的方式[31]; 二是不对小样本数据集进行处理, 在只有少量样本的情况下, 让模型适应数据, 针对数据的特点进行建模[32]. 对于小样本数据集, 设计用于提取表示能力强的特征的网络架构往往非常重要.

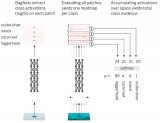
小样本图像数据集不足以让模型捕捉到足够的数据模式, 而应用于深度学习的卷积神经网络又需要大量带标签的训练样本, 因此最直接的解决办法就是进行数据增强[33]. 数据增强包括三种方式: 一是通过旋转、加噪、裁剪、压缩等操作[34], 这种数据增强的方式在处理样本不足的问题中都有应用; 二是利用生成模型生成新的样本或者生成新的特征. 例如, Jia等提出使用贝叶斯方法生成新的样本[35]. 生成对抗网络可为训练样本提供更多的生成图像, 增加训练样本的多样性. 2017年Mehrotra等提出了生成网络 + 孪生网络的网络结构[36], 生成对抗网络由生成器和判决器组成, 如图2所示, 利用生成器进行数据增强, 孪生网络用于判决器. 孪生网络第一次被Bromley等在1993年提出并用来解决一种匹配问题的签名验证[37]; 三是通过函数变换, 将图像中需要关注的物体本身或者其模式通过某种变换, 达到增加样本数量或者特征数量的目的. 例如, Dixit等利用含有属性标注的语料库来生成新的样本[38]. 如果收集到的数据包含少量带标签的样本和大量未带标签的样本, 可以利用带标签的样本去标注未带标签的样本, 产生的伪样本也可以作为增加的训练样本[39].

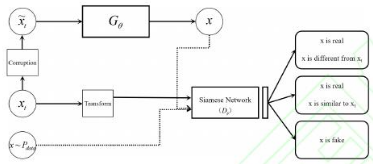
图 2  生成对抗网络 + 孪生网络[36]

Fig. 2  Generative adversarial networks + siamese networks[36]

1.1.2   特征提取

这个过程主要是为适应数据分布建立特征提取模型, 该模型能够提取图像的有效特征, 图像特征的有效性可解释为, 对于一个模型, 提取到的图像特征可以对图像进行有效表示, 达到更好的分类效果. 为了提高图像特征的有效性, 注意力机制[31]、记忆力机制[34]等技术被应用于小样本图像分类算法中.

1)注意力机制

注意力机制是人类视觉所特有的大脑信号处理机制, 人类视觉通过快速扫描全局图像, 获得重点需要关注的目标区域, 然后抑制其他无用信息, 极大地提高了视觉信息处理的效率与准确性. 注意力模型在图像领域被广泛使用, 它借鉴了人类的注意力机制, 在对图像的处理过程中, 始终关注感兴趣的部分区域, 因此在建立提取图像特征模型的过程时, 注意力机制扮演着将图像信息进一步提取为有效信息的角色, 学习不同局部的重要性.

注意力机制在数学形式上可以理解为加权求和, 通常情况下使用Softmax形式, 并通过引入新的参数来弥补模型的拟合能力. 文献[40]在对图像特征提取的过程中使用了单一注意力机制, 文献[41]认为单一的注意力机制对图像信息的提取不够充分, 提出利用多注意力机制将类别标签信息与视觉信息联系起来, 减小视觉信息与语义信息之间的鸿沟.

2)记忆力机制

循环神经网络(Recurrent neural network, RNN)解决了短期记忆的问题, 其变体长短期记忆网络(Long short-term memory, LSTM)解决了短期记忆和长期依赖的问题. 在图像领域, 基于LSTM的记忆力机制近年来发挥着重要作用, 它增强了模型的拟合能力和图像特征的表示能力. 小样本图像分类算法对于记忆力机制的应用可分为两类, 一是直接利用LSTM对图像进行编码, 提高图像特征的表示能力[9]; 二是利用读写控制器对记忆信息进行写入和读出[42].

1.1.3   分类器

分类器的设计取决于图像特征的有效性和分类器与图像特征之间的适应性. 分类器与图像特征之间的适应性可解释为, 在假定图像特征具有有效性的前提下, 分类器能够最大程度地区分不同类别的图像特征. 通常小样本图像分类中所使用的分类器, 大多数是在卷积神经网络的最后一层构建带有Softmax的全连接层, 或者对提取的图像特征应用K近邻(K-nearest neighbor, KNN)算法, 还有对分类器的权重进行重新生成, 使模型同时适用于基类数据集和新类数据集, 目前现有的元学习方法一般不研究将基类和新类一起进行分类的问题.

分类器本质上是对特征进行相似性度量并对不同类别进行最大程度的区分. 传统机器学习中最简单的度量方式KNN, 可对每个样本间的距离进行度量, 然后进行相似性距离排序, 例如, 可以利用1-nearest neighbor, 即1-NN来完成One-shot learning任务, 但实验表明分类效果并不好[43]. 除此之外, 还可以通过支持向量机(Support vector machine, SVM)进行分类度量[44-46]. 近邻成分分析(Neighborhood component analysis, NCA)[47]及其非线性方法[48]、基于集合的弱度量方法[49]等都是样本特征度量工作的范畴. 在小样本图像分类任务中, 也有利用余弦距离和欧氏距离以及点乘方式对特征距离进行度量.

一般地, 当模型学习到新的类别后, 会忘记之前学习过的类别, 与之前所做工作不同的是, Gidaris等[50]提出了基于注意力机制的分类器权重生成器, 通过重新设计分类器来适应分类器权重和图像特征之间的匹配程度, 使模型同时适用分类基类和新类样本. 类似于上述工作, Chen等[51]将线性分类器替换为基于距离的分类器, 以比较两种分类器在不同数据集上的优劣.

1.2   数据集及分类指标

1.2.1   小样本公用数据集介绍

近年来, 现有文献中的小样本公用数据集主要包括: Omniglot[52]、CIFAR-100[53]、Mini-ImageNet[9]、Tiered-ImageNet[54]和CUB-200[27]. 从数据量级的大小来看, 数据集Tiered-ImageNet, 不仅数据量级较大、类别多, 而且每类包含的样本也多; 量级较小的数据集, 例如Mini-ImageNet数据集、CIFAR-100数据集、CUB-200数据集, 这类数据集类别较少、类内样本数相对较多; Omniglot数据集类别较多, 但是相对类内样本少. 从数据类型的复杂度来看, Omniglot数据集属于字符类型的图像, 包含的类型和模式较为简单, 对其进行实验往往分类精度较高; 其他数据集都属于自然图像, 包含的图像模式较为复杂, 对其进行实验分类精度往往相对较低.

上述数据集的相关信息如表1和图3所示. 小样本图像分类使用的公用数据集图像类别均达到或超过100类, 总体数据量均超过10000, Tiered-ImageNet数据集达到77多万, Omniglot数据集和CUB-200数据集的平均类内样本数未达到100, Tiered-ImageNet数据集的平均类内样本数超过1000. 从本文第3节的实验分析将看到, 类别越多, 类内样本越多, 越有利于进行小样本图像分类, 这表明数据量级的大小对小样本图像分类结果具有一定的影响.

表 1  小样本公用数据集的数量信息

Table 1  Quantitative information of small sample public data sets

数据集	数据数量	类别数量	平均类内样本
Omniglot[52]	32460	1623	20
CIFAR-100[53]	60000	100	600
Mini-ImageNet[9]	60000	100	600
Tiered-ImageNet[54]	778848	608	1281
CUB-200[27]	11788	200	58

| 显示表格

图 3  小样本公用数据集样本示例

Fig. 3  Sample examples of small sample public data sets

1.2.2   评价指标

小样本图像分类算法的实验评价指标通常称为N-way K-shot[9]. 也有使用top-1和top-5来评价图像分类精度[55]. N-way K-shot: 选取N类图像样本, 每类图像选取K个样本或样本对, 一般地, N∈{5,10,15,20},K∈{1,5}N∈{5,10,15,20},K∈{1,5}. 模型训练阶段, 构建好训练模型并在选取的N×K个样本或样本对上进行训练; 在验证阶段和测试阶段, 选取N类样本中的K个样本或者样本对, 执行N-way K-shot分类任务. 根据预测结果来确定预测类别, 预测类别与实际类别相符的准确率即为评价指标. Top-1: 指预测排名第一的类别与实际结果相符的准确率. Top-5: 指预测排名前五的类别包含实际结果的准确率.

2.   小样本图像分类算法

针对不同类型数据的建模方式, 本文将小样本图像分类算法分为卷积神经网络模型和图神经网络模型. 根据学习范式, 卷积神经网络模型可分为迁移学习、元学习、对偶学习和贝叶斯学习. 基于迁移学习的小样本图像分类有三种实现方式, 基于特征、基于相关性和基于共享参数; 基于元学习的小样本图像分类有三种实现方式, 基于度量、基于优化和基于模型; 基于对偶学习的小样本图像分类有两种实现方式, 一是利用自动编码机, 二是利用生成对抗网络. 本节将对以上小样本图像分类算法进行详细介绍, 并在Omniglot数据集、Mini-ImageNet数据集、CIFAR-100数据集和CUB-200数据集上进行实验分析.

2.1   迁移学习

利用迁移学习[56-57]可以减小模型训练的代价, 同时达到让卷积神经网络适应小样本数据的目的. 迁移学习的思想是, 相似任务之间的学习是有相同规律可寻的, 并且学习第n个任务比第1个任务要更为简单[58]. 迁移学习关注的是目标任务, 给定一个源域DsDs和一个学习任务TsTs, 一个目标域DtDt和一个学习任务TtTt, 迁移学习的目的是使用在DsDs和TsTs上的知识帮助提高在目标域DtDt上的预测函数ft(x)ft(x)的学习, 以更好地执行学习任务TtTt, 其中Ds≠DtDs≠Dt或Ts≠TtTs≠Tt. 如果迁移学习中的源数据和目标数据不同但是具有相关性[59], 则需要进一步处理. 比如, 使用多源域的决策知识预测目标域的样本标签[60].

如图4所示, 从小样本图像分类的流程来看, 迁移学习是在图像特征提取阶段实现的. 具体的迁移方式可以分为基于特征的迁移、基于共享参数的迁移和基于关系的迁移. 如果将基类作为源域数据, 将新类作为目标域数据, 以基类数据到新类数据的知识迁移为例, 基于特征的迁移是找出基类数据和新类数据之间共同的特征, 通过特征变换的方式将基类数据的知识进行迁移, 用于新类数据分类. 该方法存在的难点在于, 一是寻找基类数据和新类数据的共同特征, 二是采用何种方式对特征进行迁移; 基于关系的迁移是建立基类数据和新类数据之间相关知识的映射, 通过这种关系映射来进行学习. 该方法的难点在于, 一是如何确定映射关系, 二是如何建立映射关系; 基于共享参数的迁移需要找到基于基类数据模型和基于新类数据模型之间的共享参数或者相同的先验分布, 利用这些参数或者先验分布进行知识迁移. 该方法的难点在于如何寻找共享参数和确定先验分布. 在寻找源域数据和目标域数据的共同特征、知识映射关系以及模型的共享参数和先验分布时, 重要的是搭建能够有效提取图像特征的网络结构以及适用的知识迁移方式. 需要建立可持续学习的模型时, 小样本迁移学习不仅需要保证模型对目标域数据有效, 而且还要确保模型在源域数据和目标域数据都有不错的分类效果.

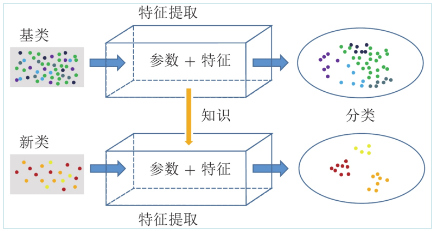
图 4  迁移学习

Fig. 4  Transfer learning

2.1.1   基于特征的迁移学习

Hariharan等[61]利用基类样本间的模式对新类样本进行相同变换, 达到增加训练样本数量的目的. 具体来讲, 从类A中抽取两个样本, 这两个样本间存在某种变换模式, 再从类B中取出一个样本, 对这个样本实施和类A中两个样本间同样的变换模式以生成新的样本. 该方法使用ImageNet1k数据集, 将其分为基类数据集和新类数据集, 基类中含有大量训练样本, 新类含有少量训练样本. 训练模型分为两个阶段, 一是表征学习阶段, 对数据增强后的基类数据进行特征提取, 并构建分类器; 二是小样本学习阶段, 利用基类数据和新类数据共同训练模型, 以获取基类数据和新类数据的共同特征, 并将表征学习阶段提取的特征用于对基类和新类进行分类. 为了使分类器同时适应基类数据和新类数据, 如式(1)所示, 提出一个新的损失函数, 用来减小模型

Loss=minW,ϕLD(ϕ,W)+λLSGMD(ϕ,W)Loss=minW,ϕLD(ϕ,W)+λLDSGM(ϕ,W)

(1)

在基类和新类上学习能力的差异, 其中, LD(ϕ,W)LD(ϕ,W)表示在基类数据上的损失, 平方梯度(Squared gradient magnitude, SGM)损失LSGMD(ϕ,W)LDSGM(ϕ,W)表示基类与新类之间的差异所造成的损失, 参数λλ通过交叉验证确定, 以保证构建一个在基类和新类都适用的分类器. Choi等[62]针对素描图像和自然图像的小样本学习问题提出了一种结构性集合匹配网络(Structured set matching networks, SSMN), 利用的是样本间的相关性. 该模型在自建的多标签的素描图像集合、自然图像集合、素描和自然图像混合的集合间的三个数据集中都有不错的效果. 它利用图像的多标签信息进行域内或跨域迁移, 通过CNN和双向LSTMs对基类样本和新类样本的局部特征进行提取并映射进同一空间中, 计算局部和全局相似度实现图像分类.

2.1.2   基于关系的迁移学习

将知识压缩进一个单一的模型已经被Buciluaana等证明是可行的[63], 进一步地, 2014年Hinton等首次提出了知识蒸馏的概念[64], 通过引入相对复杂的教师网络, 来诱导精简、低复杂度的学生网络的训练, 将知识从教师网络中迁移到压缩的学生网络中[65], 实现知识迁移. 学生网络可以通过对教师网络进行修剪[66-68]或者压缩[69-72]得到, 也可以重新设计一个新的网络架构. 知识蒸馏的目的就是在减少网络架构的同时把网络的知识保留下来, 为了达到这一目的, 提出了一个新的温度参数Tem, 将输出的概率(硬目标)进行软化, 如式(2)所示,

q=exp(ziTem)∑iexp(xiTem)q=exp(ziTem)∑iexp(xiTem)

(2)

其中zizi是Softmax层的前一层输出, qq是软化后的概率输出(软目标). 教师网络的预测输出除以温度参数Tem之后, 做Softmax变换, 可以获得软化的概率分布(软目标), 数值介于0 ~ 1之间, 取值分布较为缓和, 即对于样本的所属类别分别给出一个或大或小的概率, 而不是确定的0或1. TemTem数值越大, 分布越缓和; 而TemTem数值减小, 容易放大错误分类的概率, 引入不必要的噪声. 针对较困难的分类或检测任务, TemTem通常取1, 确保教师网络中正确预测的贡献. 硬目标则是样本的真实标注, 可以用One-hot矢量表示. 总体的损失设计为软目标与硬目标所对应的交叉熵的加权平均, 其中软目标交叉熵的加权系数越大, 表明迁移诱导越依赖教师网络的贡献, 这对训练初期阶段是很有必要的, 有助于让学生网络更轻松地鉴别简单样本, 但训练后期需要适当减小软目标的比重, 让真实标注帮助鉴别困难样本. 另外, 教师网络的推理性能通常要优于学生网络, 而模型容量则无具体限制, 因此带有标签的训练数据越多, 教师网络推理精度越高, 越有利于学生网络的学习. Kimura等[39]在2018年提出了一种不同于之前的知识蒸馏方法, 仅仅需要使用少量的训练样本就可以实现知识迁移. 利用少量可得的带标签的训练样本训练一个高斯过程的模型作为教师网络, 以克服过拟合问题, 接着如同知识蒸馏一样, 将模型中的知识迁移到学生网络模型中, 同时使用诱导点[73]作为增加的训练样本, 对学生网络进行训练. 2019年有研究人员提出在学生网络中添加1×1卷积层[74], 实现知识蒸馏[75]. 该算法使用预训练模型VGG或者ResNet等作为教师网络, 在学生网络中添加1×1卷积层, 进一步减少参数的数量, 保持特征映射尺度不变的同时增加网络的非线性, 使用最小二乘回归将其与教师网络进行对齐, 即对学生网络进行诱导学习, 经过网络训练后得到最终的学生网络.

2.1.3   基于共享参数的迁移学习

Oquab等[76]采用微调策略. 该算法中, 对图像进行多块分解实现数据增强, 加强了模型以局部视角识别图像的能力. Oquab等认为卷积神经网络提取的中层特征能够对图像进行很好的表示, 利用在ImageNet数据集上预训练的模型[8], 对图像中层特征进行提取, 并重新构建分类层, 构建新的网络对数据集分类.

Qi等[77]提出将迁移学习和增量学习进行结合, 通过对分类器的权重进行处理来实现增量零训练. 该算法利用卷积神经网络作为特征提取器以共享参数, 对新样本进行特征提取后, 产生一个分类权重向量, 将其扩展进预训练的分类器权重中, 以适应对新样本的分类任务.

除了将迁移学习与增量学习进行结合, 也可对特征提取器与分类器间的映射关系进行独立建模. Qiao等[55]在2018年提出直接从激活函数层预测分类参数的算法(Predicting parameters from activations, PPA), 一般地, 最后一层激活函数层与分类层间有相应的权重连接, 在激活函数和分类层之间建立一个分类参数预测器, 可以更好地对分类器的参数进行调整, 匹配图像特征与分类器.

2.2   元学习

元学习又叫做学会学习, 是机器学习领域一个重要的研究方向, 它解决的是学会如何学习的问题. 传统的机器学习研究模式是: 获取特定任务的数据集, 每次再利用这些数据集从头开始训练模型. 然而, 人类可以通过获取以往的经验, 对同类型的任务或有共性的任务进行快速学习, 这是因为人类懂得如何学习. 如图5所示, 如果把特征提取视为机器在数据集上学习的过程, 那么元学习器就是要评估这个学习过程, 也就是让机器学习学习的过程, 即通过学习获得学习经验, 利用这些经验再去对最终的目标任务进行评估. 一种常见的元学习方式是将学习算法编码进卷积神经网络中, 包括基于距离度量的元学习和基于模型的元学习. 基于距离度量的元学习将图像映射到一个度量空间并使用某种度量方式计算不同图像样本的差异, 度量方式包括固定距离度量[40] (欧氏距离、余弦距离或点乘)和非固定距离度量[62] (例如使用Sigmoid计算距离得分); 基于模型的元学习通过构建元模型来获得经验知识[78], 再利用这些经验去评估最终的分类任务. 另一种元学习方式是基于优化的元学习, 基于优化的元学习目的是使网络具有一个好的初始化[79].

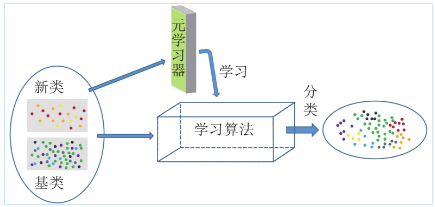
图 5  元学习

Fig. 5  Meta learning

2.2.1   基于度量的元学习

采用固定距离度量方式. 2015年Koch等[43]针对字符识别提出了深度卷积孪生网络, 利用全局仿射变换增加训练数据集. 该算法训练一个孪生网络对样本进行相似性判决, 即让样本对通过完全相同的网络结构, 利用欧氏距离对从样本中学习到的特征进行相似性度量, 根据学习到的特征映射测试样本进行分类. 虽然该方法提出不依赖先验知识, 易于简化模型, 但是缺少先验知识的辅助信息, 在较为复杂的数据集上进行小样本图像分类任务时难以达到好的效果. Vinyals等使用余弦距离度量, 设计的匹配网络(Matching networks, MN)[9]经由基于深度特征的度量学习和外部存储器增强的神经网络启发, 可以从小数据集中快速地学习新的概念, 同时避免微调, 且对细粒度图像分类(Fine-gained image classification)任务有很好的适应性. 匹配网络采用“episode” 的形式, 即从原始数据中采样出带有标签的任务集合, 然后从任务集合中获取支持集和目标集构成元任务, 通过对支持集的训练, 来最小化目标集上的误差, 很多元学习的文章对数据集都采取“episode” 的形式. 通过使用注意力机制和用于上下文嵌入的双向长短期记忆网络(Long-short term memory, LSTM)[80], 对图像特征进行充分提取. 计算测试样本标签的数学表达式如式 (3),

y^=∑i=1ka(x^,xi)yiy^=∑i=1ka(x^,xi)yi

(3)

其中xi,yixi,yi, 是来自支持集S=(xi,yi)ki=1S=(xi,yi)i=1k的样本及其对应标签, xˆx^代表测试样本. 可以看出测试样本标签的输出是支持集中标签的线性组合, aa是一个注意力机制, 通过在余弦距离上使用Softmax来实现, 可认为是对于标签的加权系数, 用来衡量支持集中训练样本和测试样本的相关程度. Bartunov等[40]在2018年提出了一种生成式匹配网络(Generative matching networks, GMN), 认为新样本的生成服从某一条件概率分布, 使用该分布生成新样本来进行数据增强, 增加了样本的多样性, 因此不要求训练数据本身具有丰富的多样性, 少量的数据即可进行小样本图像分类任务. 与之前的匹配网络不同, 该方法不是针对样本进行直接匹配, 而是将样本映射到语义嵌入空间, 在嵌入空间中利用条件似然函数对样本的语义特征向量进行匹配, 减小了特征空间和语义空间的鸿沟. Cai等[42]提出了端到端的记忆匹配网络(Memory matching networks, MMN), 是一种利用内部存储来进行记忆编码的元学习方法, 它将提取到的图像特征用记忆写入控制器压缩进记忆间隙, 然后利用上下文学习器, 即双向的LSTM对记忆间隙进行编码, 不仅提高了图像特征的表示能力, 而且能够探索类别之间的关系, 其输出为未标注样本的嵌入向量, 记忆读入控制器通过读入支持集的嵌入向量, 将两者点乘作为距离相似度度量, 相比于余弦距离, 计算复杂度更加简单. Snell等提出的原型网络(Prototypical networks, PN)[29]需要计算类别原型. 通过学习一个度量空间, 在这个度量空间内, 分类器可以根据样本到类别原型间的距离, 来对样本进行分类. 每个类别原型, 可以通过对每个类别中所有样本在度量空间的向量求平均得到, 使用欧氏距离来判断样本所属的类别.

Choi等采用非固定距离度量[62], 针对素描图像和自然图像的小样本图像分类问题提出了一种结构性集合匹配网络(Structured set matching networks, SSMN), 从执行任务的角度来看该方法属于元学习. 该模型利用RNN对图像间的所有标签对应的局部信息进行局部相似度计算, 并将局部特征和全局特征进行结合, 利用多标签数据增强图像的解释性, 但同时也增加了标注数据的工作量. 人类在辨别事物的时候, 习惯对不同的事物进行比较, 根据这个简单的思想, Sung等[30]在2018年提出的端到端的相关网络(Relation network, RN), 学习一个深度距离以度量元学习任务的不同样本. 相关网络由两个模块组成, 嵌入模块和相关模块, 嵌入模块对不同的样本进行特征提取, 相关模块将不同样本的特征进行拼接进而得出不同样本间的相关性度量分数. Zhou等[81]提出了基于嵌入回归的视觉类比网络, 学习低维的嵌入空间, 再从嵌入空间中学习到分类参数的线性映射函数, 对新类分类时, 将新类样本与学习到基类的嵌入特征进行相似度度量.

2.2.2   基于模型的元学习

一般地, 元学习分为两个阶段: 执行在不同任务上的元级模型的慢速学习和执行在单个任务中的基准模型的快速学习[82-83], 元级模型的目的是学习不同任务中的通用知识, 然后将其传递给基准模型, 来帮助在单个任务上的学习. Munkhdalai等[78]在2017年使用卷积神经网络构造了一种元网络(Meta networks, meta-Nets), 用于跨任务间的学习, 遵循之前的工作, 将元学习问题分为两个阶段. 它提出了一种更快的学习方法是利用一个神经网络去预测另一个神经网络的参数, 生成的参数称为快权值, 用来加快网络的学习速度, 普通的基于随机梯度下降(Stochastic gradient descent, SGD)等优化的参数被称为慢权值. 该模型的训练由元级模型和基准模型共同来执行, 包括元信息的获取, 快权重的产生和慢权重的更新. 基准模型使用损失梯度信息作为元信息, 在不同元任务中获取元信息并存储在外部设备. 元级模型对存储在外部存储设备的元信息进行获取, 并通过预测产生快权值来加速网络学习. Zhou等[32]在2018年提出的深度元学习模型(Deep meta learning, DML), 能够在概念空间中进行学习, 而不是在传统上的视觉空间. 该模型由三个模块组成: 概念生成器、元学习器和概念判决器. 为了让元学习有一个好的特征表示, 概念生成器使用深度残差网络, 以捕捉高级语义概念, 然后利用概念判决器进行信息反馈和优化, 同时将提取到的特征作为概念用于元学习器进一步地学习. 该方法通过在语义概念上的学习减少了视觉空间和语义空间的鸿沟, 使用深度残差网络来构建更加复杂的模型, 以适应复杂的数据模式. Santoro等[34]提出利用RNN架构加外部存储记忆的方式. 外部存储的使用使模型精度获得了提高, 但是同时也降低了模型的效率并占用了大量的存储空间. Sun等[84]提出的元 − 迁移学习(Meta-transfer learning, MTL)利用迁移知识有效减少模型更新的参数, 同时构建更深层次的网络增加模型的复杂度.

元学习模型通用方法. 针对小样本数据量较少的特点, Wang等[85]在2018年提出了对于任何元学习模型都适用的数据增强方式, 针对生成模型捕捉的样本模式不足这一问题, 提出使用生成模型来产生新的样本, 这些样本是由真实的样本和噪声向量通过3层带有Relu非线性激活函数的多层感知机(Multi-layer perception, MLP)产生的, 利用生成的样本和原有的样本共同对模型进行训练. 该数据增强方式能够结合任何元学习算法进行使用, 由于采用生成网络产生新样本, 因此实验结果的好坏取决于生成新样本的质量. Wang等[86]提出了一个模型回归网络(Model regression networks), 利用的是分类器之间的相关性. 该方法认为在小样本数据中学习到的分类器和在大样本数据中学习到的分类器之间存在一种变换, 可以通过深度回归网络进行学习, 同时该变换作为一种先验知识可以帮助在小样本数据上的分类任务.

2019年有研究学者将增量学习与元学习进行结合, 提出的注意力吸引网络[87] (Attention attractor networks, AAN)模型不仅在新类上表现良好, 而且不会遗忘在基类上学习到的知识. 如图6, 训练阶段A, 在基类上进行预训练模型, 学习分类参数WaWa, 阶段B结合注意力机制并利用每次学习一个新任务的分类参数WbWb, 阶段C将WaWa和WbWb作为基类和新类的分类参数W∗bWb∗用来对元任务进行测试. 对于给定的新任务都会学习一个参数WbWb, 代表该任务在执行分类时的贡献, 使得分类器更加灵活适用, 而且对单个新样本的分类也更加容易.

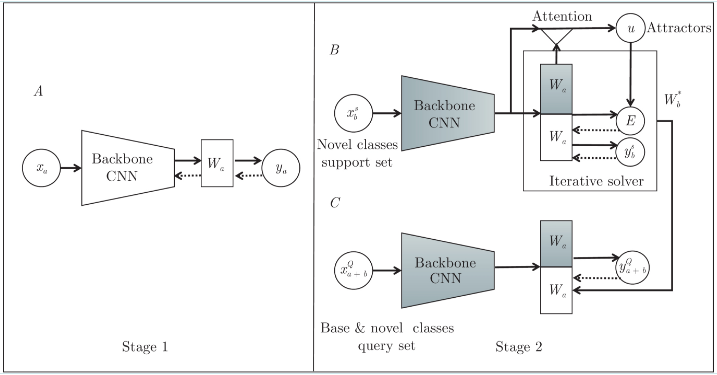
图 6  注意力吸引网络结构[87]

Fig. 6  Attention attractor networks structure[87]

2.2.3   基于优化的元学习

针对小样本数据集的微调策略, 采用的是将模型在大数据集上进行预训练, 然后在小数据集上进行简单微调. 然而经过预训练的模型并不能保证对于微调有一个很好的初始化参数. 基于优化的元学习能够保证网络学习到一个好的初始化, 使模型对新任务更易于微调.

Finn等[79]在2017年提出了一种与模型无关(Model-agnostic meta-learning, MAML)的元学习算法. 该算法提出的模型无关性元学习算法, 使用少量的梯度迭代步骤就可以学习到适用于新任务的参数, 能够匹配任何使用梯度下降法训练的模型. 简单地讲, 如果在模型中加入新的任务, 每个不同的任务会产生不同的损失, 利用模型在该任务上的损失进行参数优化, 使其快速适用于新的分类任务. 然而MAML对神经网络结构非常敏感, 导致训练过程不稳定, Antoniou等[88]提出对MAML进行优化, 进一步提高了系统的泛化性能, 加快了网络的收敛速度, 减少了计算开销. Nichol等[89]提出的基于优化的元学习模型Reptile, 也是通过学习网络参数的初始化, 与MAML不同的是, Reptile在参数优化时不要求使用微分. Ravi等[90]提出的基于梯度的优化算法, 使用基于LSTM的元学习模型去学习一个网络的初始化, 它能够捕捉到单个任务的短期知识和所有任务的长期知识, 以便更好地提取特征用于解释图像.

2.3   对偶学习

为了降低机器对大量标注样本的依赖, 以及在强化学习中减少机器与环境交互的次数, 对偶学习作为一种新的学习范式应运而生. 现实生活中, 很多有实用价值的人工智能任务往往是成对出现的, 例如, 在图像领域, 图像识别和图像生成都有重要的应用, 属于对偶任务. 如果根据对偶任务来训练模型, 利用任务到任务的反馈信息, 就能克服模型对数据的依赖问题[91].

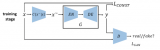
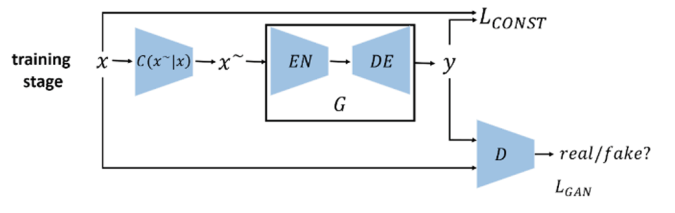
深度神经网络中的自编码机(Auto encoder, AE)就是对偶学习的一个特例, 包括两个部分: 编码和解码. 变体算法有降噪自编码机[92]、堆叠卷积自编码机[93]和变分自编码机[94]等, 其应用主要为数据去噪、数据降维以及数据生成. 在进行小样本图像分类的过程中, 由于数据量小, 会进行数据增强操作, 但是数据增强有时候会产生噪声数据, 对于样本数据的多样性表示不足, 可能不会对决策边界产生影响, 需要引入额外的语义知识. 如图7所示, Chen等[31]在2018年提出语义特征增加的算法(Semantic feature augmentation, SFA) ResNet-18 + 对偶TriNet网络, 利用编码 − 解码机制在图像特征和语义空间进行变换实现特征增加, 增加的特征能够丰富图像的语义多样性, 引入额外的语义信息. 使用ResNet-18网络对图像特征进行提取, 编码器Encoder-Trinet将提取的特征映射到语义空间, 在语义空间中, 对语义特征添加噪声进行高斯扰动, 假设语义空间中的特征值的微小变化允许在保持语义信息的同时形成潜在的类内变换, 然后采用解码器Decoder-Trinet将语义特征映射回多层的ResNet-18特征空间, 即实现特征增加. 该算法是一个端到端的网络框架, 能够在多层的图像特征空间和语义空间中学习映射关系, 适用于多种网络结构.

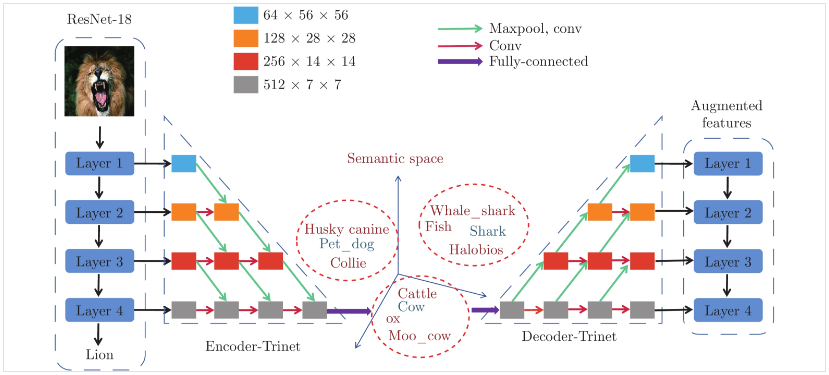
图 7  编码—解码机制[31]

Fig. 7  Coding-decoding mechanism[31]

2.4   贝叶斯学习

深度学习基于大数据通过多层网络实现对抽象概念的理解, 显然, 数据量越多其效果越好, 假如没有那么多的大数据该如何进行抽象概念的理解. 对人类来说, 即便没有知识的积累, 没有相应的专业知识, 我们也能够照猫画虎, 这有点类似贝叶斯学习的方式[95]. 贝叶斯学习是利用参数的先验分布, 由小样本信息得到的后验分布, 直接求出总体分布. 贝叶斯学习理论使用概率去表示所有形式的不确定性, 通过概率规则来实现学习和推理过程. 更具体的来说, 贝叶斯学习并不去求解最优的参数值θ,θ,而是假设参数θθ本身符合某个分布, 即先验概率P(θ),P(θ),随后利用训练样本得到条件概率分布P(X|θ),P(X|θ),根据贝叶斯公式我们便能求得样本的总体分布, 如式(4),

P(θ|X)=P(θ)P(X|θ)P(X)P(θ|X)=P(θ)P(X|θ)P(X)

(4)

其中P(X)P(X)为样本XX服从的分布. 将贝叶斯学习与深度学习结合为贝叶斯深度学习, 此时网络的权重WiWi和偏置bb由确定的值变成某种分布. Lake等在2011年提出层次贝叶斯程序学习(Hierarchical Bayesian program learning, HBPL), 对观测像素进行结构解释, 解决了字符识别的问题, 但是其参数空间太大[12], 因此, 又提出了一种基于组合和因果关系的层次贝叶斯模型[96], 解决了对大数据集的依赖问题. 在2015年的贝叶斯框架中提出了一种新的计算模型, 用来模拟人类的学习能力[52], 同时加入了元学习, 可以从现有的字符中抽象出其部件, 再根据不同部件的因果关系创造新的字符, 从而形成丰富的概念. 2018年Kim等[97]将贝叶斯方法应用在与模型无关的元学习算法中, 将基于梯度的元学习与非参数变量的推理结合起来, 使用贝叶斯先验防止元学习模型过拟合, 但也提升了模型的复杂度.

2.5   图神经网络模型

现实生活中的大量问题都可以被抽象成图模型[98], 图G=(V,E)G=(V,E)作为一种数据结构, 由节点VV和边EE的集合组成, 能够表达复杂的数据关系. 传统的机器学习方法很难处理图神经网络信息, 充分挖掘图中蕴含的知识是一项非常具有挑战的任务. 在深度学习时代, 将图与深度学习进行融合成为了一项重要的工作. 本节所述的图神经网络(Graph neural network, GNN)模型是将CNN用于图神经网络上, 并对欧几里得小样本图像数据进行分类.

图神经网络在2005年首次被Gori等[99]和Scarselli等[100]提出, 用传统的方法处理图结构数据是将其转换为一组平面向量, 然而以这种方式处理数据, 重要的拓扑信息可能丢失, GNN扩展了递归神经网络, 使有向图、无向图、循环图等得以被处理, 作为一种可训练的网络其中固定节点可被分别调整. Bruna等[101]和Henaff等[102]提出学习图拉普拉斯的光滑谱乘子, 是将CNN泛化到非欧氏空间的一种尝试, 但是其计算代价非常高. Defferrard等[103]和Kipf等[104]通过学习图拉普拉斯的多项式解决了计算代价的问题. Li等[105]和Sukhbaatar等[106]进一步放宽模型的限制, 对网络层内的权重解耦, 同时提出门控机制进行非线性更新.

在小样本学习中, 为了将图神经网络应用于规则的欧几里得图像数据, Satorras等[107]在2018年提出了一个端对端的图卷积网络结构(Graph convolutional network, GCN), 用于捕捉任务中具有不变性的特征. 图神经网络模型由输入图片的集合构成, 图神经网络中的节点与集合中的图片信息相关, 边是一个可训练的、用来度量相邻两个节点相似性的参数. 如图8所示, 将5个样本通过式(5)构建出图邻接矩阵, 接着通过图卷积得到节点的嵌入向量, 然后用式(5)依次更新图, 用图卷积更新节点嵌入, 这样就构成了一个深度的图卷积神经网络, 最后使用交叉熵损失函数计算图卷积神经网络的输出概率p.φθ˜(⋅)p.φθ~(⋅)的具体形式为式(6), 使用MLP来计算图邻接矩阵A˜(k)i,j.A~i,j(k).其中, x(k)ixi(k)和x(k)jxj(k)为输入样本. T 表示输入的学习任务.

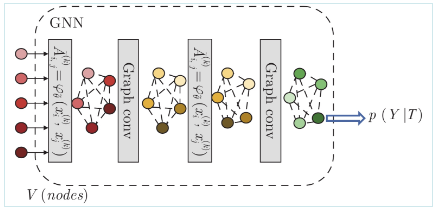
图 8  图卷积神经网络[107]

Fig. 8  Graph convolution neural network[107]

A˜(k)i,j=φθ˜(x(k)i,x(k)j)A~i,j(k)=φθ~(xi(k),xj(k))

(5)

φθ˜(x(k)i,x(k)j)=MLPθ˜(abs(x(k)i−x(k)j))φθ~(xi(k),xj(k))=MLPθ~(abs(xi(k)−xj(k)))

(6)

文献[107]利用图节点的标签信息, 隐式地对类内的相似性和类间的不相似性进行建模, 与之相反, Kim等[108]在2019年提出的基于边标签的图卷积神经网络(Edge-labeling graph neural network, EGNN), 将数据集分为多个元任务, 包括支持集和查询集, 通过直接探索类内的相似性和类间的不相似性来迭代地更新边标签信息, 通过预测边标签对样本进行显式聚类. Liu等[109]提出了一种转导式的传播网络(Transductive propagation network, TPN), 该算法利用元学习框架和流型假设, 通过对特征嵌入参数和图神经网络构建的参数进行联合学习, 将标签从标注样本传递到未标注样本, 提高了模型的泛化能力.

3.   实验对比分析

上文描述的现有基于小样本学习的图像分类算法被归纳为卷积神经网络模型和图神经网络模型两大类, 具体如图9所示.

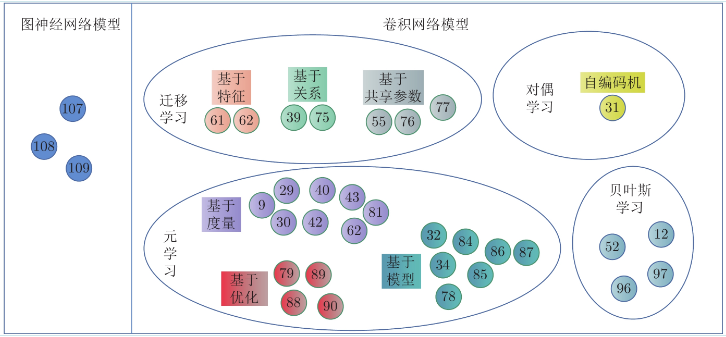
图 9  小样本图像分类算法概况

Fig. 9  Overview of small sample image classification algorithms

3.1   各种算法在公用数据集上的实验测试结果分析

1)三种基于元学习的小样本图像分类算法各有优势, 此外训练模型时学习的类别越多, 类内样本越少, 分类效果越不好.

Omniglot数据集是字符图像, 背景单一, 内容简单. 从表2中可以看出, 基于元学习的小样本算法在Omniglot数据集上的N-way K-shot分类结果非常好. 然而, 学习类别越多, 样本越少, 分类效果越不好, 因此20way-1shot的实验结果相对其他N-way K-shot分类结果较低.

表 2  基于元学习的Omniglot实验结果

Table 2  Experimental results of Omniglot based on meta learning

		Omniglot
		5way-1shot	5way-5shot	20way-1shot	20way-5shot
基于度量的元学习	MN[9]	98.12	99.63	94.40	98.78
	文献 [40]	90.80	96.70	77.00	91.00
	MMN[42]	99.28	99.77	97.16	98.93
	PN[29]	98.80	99.18	92.11	97.57
	RN[30]	99.48	99.60	97.67	98.97
基于模型的元学习	Meta-Nets[78]	98.00	99.60	96.90	98.50
基于优化的元学习	MAML[79]	98.79	99.48	93.43	95.33
	文献 [88]	—	—	97.65	99.33
	Reptile[89]	97.50	99.87	93.75	97.68

| 显示表格

小样本图像分类算法中, 基于度量的元学习算法在Mini-ImageNet数据集上学习到好的度量空间可提高分类效果. 如表3所示, 基于度量的元学习算法中, MMN使用了记忆力机制, 加强了图像特征的表示能力, 可以学习到一个好的度量空间.

表 3  基于元学习的Mini-ImageNet实验结果

Table 3  Experimental results of Mini-ImageNet based on meta learning

		Mini-ImageNet
		5way-1shot	5way-5shot
基于度量的元学习	MN[9]	44.38	57.78
	PN[29]	44.43	66.04
	RN[30]	50.13	64.33
	MMN[42]	53.37	66.97
基于模型的元学习	DML[32]	58.49	71.28
	AAN[87]	54.89	62.37
	MTL[84]	61.20	75.50
基于优化的元学习	MAML[79]	43.09	60.63
	Reptile[89]	48.21	66.00
	文献 [90]	43.44	60.00
	文献 [88]	52.15	68.32

| 显示表格

小样本图像分类算法中, 基于模型的元学习算法通过学习丰富的图像语义特征帮助在Mini-ImageNet数据集上分类. 其中, DML利用深度残差网络作为概念生成器, 可以构建表达能力更大的网络结构, 产生更好的语义特征.

小样本图像分类算法中, 基于优化的元学习算法具有快速学习的能力. 其与基于模型的元学习算法相比分类结果较差, 通过学习网络参数的初始化, 模型微调于新类时会更加适应, 该类算法能够快速对新样本进行训练, 其分类效果依赖于优化策略以及对新样本的适应.

2)图卷积网络模型中, 对类内样本的相关性和类间样本的不相关性建模, 在Omniglot和Mini-ImageNet数据集上能够产生更好的分类效果.

如表4所示, GCN、TPN以及EGNN在Omniglot数据集上都取得了很好的分类精度, 在更为复杂的图像数据集Mini-ImageNet上, EGNN的分类效果好于GCN和TPN.

表 4  基于图卷积网络的Mini-ImageNet、Omniglot实验结果

Table 4  Experimental results of Mini-ImageNet and Omniglot based on graph convolutional network

	Omniglot				Mini-ImageNet
	5way-1shot	5way-5shot	20way-1shot	20way-5shot	5way-1shot	5way-5shot
GCN[107]	99.26	99.72	97.66	99.10	53.03	64.78
TPN[109]	99.26	99.44	96.48	98.59	54.44	67.05
EGNN[108]	99.75	99.77	98.62	99.62	62.34	75.77

| 显示表格

GCN模型利用样本间的相关性建立模型, 但忽略了样本间存在的差异性. TPN对模型的建立是利用了样本间的相关性和不相关性. EGNN则利用卷积网络对样本间的相关性和不相关性进行学习, 进一步复杂化了模型, 同时增强了模型的非线性化, 提高了模型的表达能力.

3)当小样本图像分类算法提取到丰富的高层语义特征或者在特征提取和分类器之间设计好的映射函数时, 能产生较好的分类效果.

表5所示, 分别从各类中挑选出的性能最好的算法进行比较, 在Mini-ImageNet数据集上各算法的5way-1shot分类精度接近于60.0 %, 5way-5shot的分类精度均高于70.0 %, 其中SFA和EGNN达到了76.0 %, 这四种算法分别是迁移学习算法PPA、元学习算法DML、对偶学习算法SFA、基于图卷积神经网络的算法EGNN, 其中PPA算法通过激活函数来预测分类器中的分类参数, 相当于在高层语义特征和分类器之间做一个映射, 使分类器对于不同语义特征的选择更加精确; DML算法利用深度残差网络提取到图像的高级语义特征; SFA算法通过编码—解码机制, 对编码机映射到语义空间中的实例特征扰动, 再利用解码机产生丰富的图像特征. EGNN算法对类内样本关系和类间样本关系进行建模, 能够对图像信息进行强有力的表示. 可以看出, 通过对图像的高层语义特征的利用, 提高了小样本图像分类的精度.

表 5  迁移学习、元学习、对偶学习和图神经网络模型实验结果

Table 5  Experimental results of transfer learning, meta learning, dual learning and graph neural network model

	Mini-ImageNet
	5way-1shot	5way-5shot
迁移学习 PPA[55]	59.60	73.74
元学习 DML[32]	58.49	71.28
对偶学习 SFA[31]	57.95	76.64
图神经网络模型 EGNN[108]	62.34	75.77

| 显示表格

3.2   小样本学习算法在轮胎花纹数据集上的实验结果

为进一步分析现有小样本图像分类算法的表现, 本节实验在西安邮电大学图像与信息处理研究所依托与公安部门合作的平台所自建的轮胎花纹图像数据集[110]上进行.

轮胎花纹分类的研究源于交通肇事及公安案件处理中轮胎花纹匹配的实际需求. 该数据集是目前公开用于学术研究的最大的轮胎花纹数据集, 包含轮胎表面花纹数据和轮胎压痕花纹数据各80类, 每类30张不同亮度不同尺度和不同旋转角度的图片, 如图10所示. 实验测试分别在表面花纹图像数据、压痕花纹图像数据、及两种图像混合数据上进行(因为实际需求往往需要进行表面花纹和压痕花纹的比对). 实验中46类用于训练, 10类用于验证, 13类用于测试, 轮胎混合花纹数据集包含同样的类别, 不同的是每类160张图像.

图 10  轮胎花纹数据集样本示例

Fig. 10  Sample examples of tire patterns data sets

为研究基于元学习的小样本学习算法、通过编码—解码进行语义特征增强的小样本学习算法和基于图神经网络的小样本学习算法对轮胎花纹图像分类的效果, 分别对以下5个算法进行了实验: 基于优化的小样本元学习算法[79], 基于模型的小样本元学习算法[78], 基于度量的小样本元学习算法[30], 基于编码—解码结构的小样本对偶学习算法[31], 基于图神经网络的小样本学习算法[107]. 表6为实验测试结果, 通过五组实验对比可以看出:

表 6  在轮胎花纹数据集上的测试结果对比

Table 6  Test results comparison of various algorithms on tire patterns data set

算法	轮胎数据集	分类精度
		5way-1shot	5way-5shot
文献 [79]	表面	67.09	85.55
	压痕	77.66	87.32
	混合	46.03	64.00
文献 [78]	表面	53.46	78.42
	压痕	66.13	80.45
	混合	42.80	63.53
文献 [107]	表面	77.46	89.52
	压痕	77.76	92.00
	混合	58.04	79.98
文献 [31]	表面	72.71	91.03
	压痕	76.42	91.76
	混合	51.84	81.02
文献 [30]	表面	63.97	81.60
	压痕	73.71	84.54
	混合	48.21	65.20

| 显示表格

1)通过编码—解码结构进行的语义特征增强能够提高分类精度.

2) 5组实验的分类精度在混合数据集上均相对较低, 这是因为同一类轮胎混合花纹图像中包含了表面花纹和压痕花纹两种既相关又有差异的数据, 造成类间相似度降低, 从而分类任务难度增加.

相比其他算法, 基于图神经网络的小样本学习算法在轮胎花纹表面数据集和压痕数据集上的分类精度差异最小, 而且在混合花纹数据集上的分类精度最高. 这说明基于图神经网络的小样本学习算法适用于轮胎花纹数据集的分类研究. 下一步工作中, 我们将对比更多算法, 并进行更进一步的研究.

3.3   不同模型的小样本图像分类算法的讨论

针对第3.1节和第3.2节的实验分析结果, 本节进一步分析了各类算法之间的特点, 并分别对卷积神经网络模型和图神经网络模型进行讨论.

1)对卷积神经网络模型的讨论.

如表7所示, 卷积神经网络模型中的迁移学习、元学习、对偶学习都可以使用数据增强的方式来解决小样本图像分类问题, 当增强的样本具有较大的数量和丰富的语义内容时, 小样本数据集的分类结果会有所提升.

表 7  小样本图像分类算法的对比

Table 7  Comparison of small sample image classification algorithms

	算法	数据增强	训练策略	分类度量方式	数据集
基于特征的迁移学习	文献 [61]	函数变换增加训练样本	CNN 表示学习阶段 + 小样本学习阶段	全连接层 + Softmax	ImageNet
	SSMN[62]		CNN + LSTM 局部特征度量 + 全局特征度量	嵌入向量 + 点乘	DiPART、PPM、Cross-DiPART-PPM
基于关系的迁移学习	文献 [39]	采用伪样本数据	CNN 知识蒸馏	全连接层 + Softmax	MNIST
	文献 [75]		CNN 1×1卷积核知识蒸馏	全连接层 + Softmax	CIFAR-10、CIFAR-100
基于共享参 数的迁移 学习	文献 [76]	裁剪	CNN 预训练模型 + 微调	全连接层 + Softmax	PASCAL VOC 2007、PASCALVOC 2012
	文献 [77]		CNN 分类权重嵌入	全连接层 + Softmax	CUB-200
	PPA[55]		CNN 在激活函数和 Softmax 之间建模, 预测类别的分类参数	全连接层 + Softmax	Mini-ImageNet
基于度量的元学习	文献 [43]		CNN 孪生网络 + 距离度量	嵌入向量 + 欧氏距离	Omniglot
	MN[9]	仿射变换	CNN + LSTM 注意力模块 + 样本间匹配	嵌入向量 + 余弦距离	Omniglot、Mini-ImageNet
	MMN[42]		CNN + bi-LSTM 记忆读写控制模块 + 样本间匹配	嵌入向量 + 点乘	Omniglot、Mini-ImageNet
	PN[29]		CNN 聚类 + 样本间原型度量	嵌入向量 + 欧氏距离	Omniglot、Mini-ImageNet
	RN[30]	旋转	CNN 不同样本在特征空间比较	全连接层 + Softmax	Omniglot、Mini-ImageNet
	文献 [81]		CNN 利用嵌入特征回归分类参数 + 不同样本映射到同一嵌入空间进行相似性度量	全连接层 + Softmax	Omniglot、Mini-ImageNet
基于优化的元学习	MAML[79]	旋转	利用基于梯度的学习来更新每个元任务的参数		Omniglot、Mini-ImageNet
	Reptile[89]		将梯度下降计算的参数与初始化参数的差用于参数梯度更新		Omniglot、Mini-ImageNet
	文献 [90]		利用 LSTM 模型学习优化算法		Mini-ImageNet
基于模型的元学习	Meta-Nets[78]	旋转	CNN + LSTM记忆模块 + Meta learner + Base learner	全连接层 + Softmax	Omniglot、Mini-ImageNet
	DML[32]		CNN 概念生成器 + 概念判决器 + Meta learner	全连接层 + Softmax	CUB-200、CIFAR-100、Mini-ImageNet
	文献 [34]		CNN + LSTM对样本和标签进行绑定编码使用外部记忆存储模块	全连接层 + Softmax	Omniglot
基于模型的元学习	文献 [85]	函数变换增加训练样本	CNN 利用数据增强提升元学习	全连接层 + Softmax	ImageNet
	文献 [86]		CNN 减小大数据集和小数据集分类器间的差异	SVM	CUB-200
	AAN[87]		CNN 注意力模块 + 增量学习 + 元学习针对样本生成相应的分类参数	全连接层 + Softmax	Mini-ImageNe、Tiered-ImageNet
自动编码机	SFA[31]	使用编码 − 解码机制进行特征增加	CNN 通过扰动语义空间特征实现样本特征增加	全连接层 + Softmax	CUB-200、CIFAR-100、Mini-ImageNet
图卷积神经网络	GCN[107]		GCN 利用图节点标签信息, 隐式地对类内和类间样本关系进行建模	全连接层 + Softmax	Omniglot、Mini-ImageNet
	EGNN[108]		GCN 通过预测边标签, 显式地对类内和类间样本进行建模	全连接层 + Softmax	Mini-ImageNet、Tiered-ImageNet
	TPN[109]		GCN 流型假设 + 标签传播	全连接层 + Softmax	Mini-ImageNet、Tiered-ImageNet

| 显示表格

对偶学习目前在小样本图像分类中的主要应用是数据增强, 不同于之前的图像变换方法, 对偶学习中可以利用自编码机在图像的视觉特征空间和语义特征空间之间相互变换, 它可以和现有的图像特征提取模型进行结合, 利用自编码机寻找好的数据增强方式.

相对于迁移学习、元学习和对偶学习, 贝叶斯学习目前在小样本学习中的应用较少, 可以更好地应用于训练数据量较少的情况, 但需要指定参数的先验分布, 而且对于样本的独立性要求较高, 但是现实生活中的样本和类别都具有一定的相关性, 因此建模方式存在偏差, 可将其与其他小样本图像分类方法相结合.

目前小样本图像分类中应用最多的是迁移学习和元学习, 两种方法都可以借助预训练模型来进一步学习, 或者借助迁移学习思想和元学习策略对小样本数据进行训练, 迁移学习更多侧重于得到表示性更强的迁移特征, 元学习在度量方式、模型设计以及初始化策略上都有考量. 同时, 对传统机器学习分类器的使用也使得模型的解耦性增强, 更好地进行网络架构的设计, 其中基于欧氏距离、余弦距离和点乘方式度量在基于度量的元学习中使用较多.

2)对图神经网络模型的讨论.

本文所述的图神经网络模型利用CNN对欧几里得图像数据进行特征提取, 由于图神经网络模型的节点和边可以表示更多的图像信息, 因此图神经网络对于样本间的复杂关系有更强的表示能力, 也有助于探索更多潜在于小样本数据集中的信息. EGNN相比较于GCN和TPN其模型的复杂度更高, 体现在对图中相邻节点关系的表示上, EGNN不仅利用了类内样本间的相关性, 而且也对类间样本的不相关性进行建模, 再通过迭代不断地学习类内相关性和类间不相关性. 从表4中可以发现, 其在Mini-ImageNet数据集上的5way-5shot分类精度达到了75.77 %. 图神经网络对数据的建模方式与卷积神经网络模型不同, 它能够将图像间的联系以图连接的形式呈现出来, 图中的边可以显式表达这种联系, 图模型构建以及图的更新方式目前还有待更多研究.

4.   技术挑战与未来研究趋势

目前, 小样本图像分类算法在模式较为简单的字符型数据集Omniglot上已取得很好的分类结果, 但是对于相对复杂的数据集, 虽然分类结果不断提升, 但是仍然不理想. 利用数据增强、正则化、对特征提取过程建模等方式, 可以有效地缓解小样本带来的过拟合问题, 也能够增强图像特征的表示能力, 但仍然需要在克服过拟合问题和增强图像的表示能力之间进行权衡. 除此之外, 小样本图像分类仍然面临一些挑战, 本节将对此进行介绍, 同时从技术角度对小样本图像分类未来的研究趋势进行展望.

4.1   小样本图像分类面临的挑战

1)权衡过拟合问题和图像特征表示能力

小样本图像分类模型往往需要克服过拟合问题, 同时又要从少量的样本中学习到能够表示图像的有效特征. 迁移学习中对小样本数据集进行特征提取[61], 元学习中从元任务中获取元信息[29]等都需要对图像特征进行提取, 为了缓解过拟合问题, 通常使用的网络结构较为简单, 不足以对图像中蕴含的信息进行有效表达, 而Resnet网络[87]和其他残差网络[32]能够加深网络的层数, 记忆模块能够对历史信息进行存取和使用[34, 62, 78, 90], 从而增强了图像特征的表示能力. 因此, 如何权衡过拟合问题和图像特征表示能力是小样本图像分类需要面临的挑战.

2)不同应用领域的小样本图像分类

从上述的实验分析中可以看出, 多数小样本图像分类算法, 在模式简单、背景单一的字符型数据集Omniglot上具有非常好的分类效果[30, 79, 89], 在模式较为复杂的其他类型的数据集, 同一个小样本图像分类算法在不同的小样本数据集上的分类结果具有一定的差异[31-32]. 针对不同应用领域图像数据内容的不同特点, 如何设计合适的小样本图像分类算法, 或者具有一定普适性适应不同数据集的算法, 这也是小样本图像分类目前的难点.

4.2   小样本图像分类未来的研究方向

1)应用注意力机制

小样本学习的训练样本量较少, 提取到的信息相对有限, 可以利用注意力机制在有限的训练样本下, 提取到对图像具有表示性更强的特征, 并且使得该特征能够显著影响分类效果. 小样本学习从本质上讲是想让机器学会人类的学习方式以及泛化能力, 人类能够在图像识别任务中很好地利用注意力机制, 此外, 注意力机制能够提高神经网络的可解释性[111], 软注意力机制和硬注意力机制[112]、自注意力机制[113]、互注意力机制[114]等注意力模型, 其直观性、通用性以及可解释性能够对小样本图像分类任务提供重要帮助.

2)将CNN中图像特征的标量表示替换为向量表示

CNN利用卷积核能够检测出相应的图像特征, 但如果样本不够丰富, 一些重要信息就会检测不到, 比如位置等信息, 因此, CNN需要更多的样本来增强它的性能, 提高图像特征的表示性. 胶囊网络通过向量来对图像特征进行表示, 向量中可以包含任意个值, 每个值代表当前需要识别的物体的一个特征, 而传统的卷积操作是通过线性加权求和的结果, 得到的是标量. 胶囊网络利用动态路由算法进行信息传递, 它需要较少的训练数据, 而且能够保留图像特征的位置和姿态信息, 对旋转、平移以及其他仿射变换也有很强的鲁棒性[115].

5.   结束语

本文针对当前基于小样本学习的图像分类算法进行了归类总结, 依据对不同数据类型的建模方式, 将小样本图像分类算法分为卷积神经网络模型和图神经网络模型两大类, 其中, 卷积神经网络模型又分为迁移学习、元学习、贝叶斯学习和对偶学习四种学习范式, 并针对数据集处理、特征提取和分类器设计三个环节, 对两类算法进行了详细介绍. 迁移学习更多侧重于得到表示性更强的迁移特征; 元学习在度量方式、模型设计以及初始化策略上都有考量; 贝叶斯方法目前难以单独应用于小样本图像分类; 对偶学习应用于小样本图像分类的是编码—解码结构, 可进行数据增强; 图神经网络可侧重于对图像间关系进行建模. 最后针对目前小样本图像分类算法的不足, 分析了小样本图像分类面临的挑战, 同时从技术角度探索了小样本图像分类的未来研究趋势.

 

【转载声明】转载目的在于传递更多信息。如涉及作品版权和其它问题，请在30日内与本号联系，我们将在第一时间删除！

关注微信公众号：人工智能技术与咨询。了解更多咨询！

编辑：fqj