中利用无限循环将程序控制在主程序函数中,就出现了前面实验结果中令人迷惑的情况。
注:他是一个胆大心细的人,观察还挺仔细的。
摘要: 智能飞行器航迹规划问题是一个大范围多目标多约束的三维规划问题,这类问题可以归属于路径规划问题,在满足相应条件的同时要求在较短的时间内以较短的路程到达目的地。本文把航迹的约束条件转化到实际问题中,通过对A*算法的改进,建立起符合飞行器航迹规划的两种算法模型。通过两种方案算法的比较,在两种情况下,算法程序实现得到航迹规划结果表和路径图。算法的有效性和复杂度分析结果表明,给出的求解算法是十分有效的。
1. 引言
智能飞行器飞行操作的多约束环境下的航迹快速规划优化技术,是研究智能飞行器控制的一个重要问题。但是由于系统结构的设置产生的限制,这类飞行器的定位系统,对自身进行精准定位无法进行,定位误差如果累计到一定程度,就可能导致整体任务失败。所以在飞行过程中对定位误差进行校正,是智能飞行器航迹规划中一项重要步骤 [1]。本文研究智能飞行器在系统定位精度限制下的航迹快速规划问题,即如何在轨迹规划的过程中,将定位误差限制在可接受范围内,保证任务的顺利完成。
假定飞行器的出发点为A点,目的地为B点。其航迹约束如下:
(1) 飞行器在空间飞行过程中需要实时定位,其定位误差包括垂直误差和水平误差。飞行器每飞行1m,垂直误差和水平误差将各增加 δδ 个专用单位,,以下简称单位。到达终点时垂直误差和水平误差均应小于个单位,并且为简化问题,假设当垂直误差和水平误差均小于 θθ 个单位时,飞行器仍能够按照规划路径飞行。
(2) 飞行器在飞行过程中需要对定位误差进行校正。飞行区域中存在一些安全位置(称之为校正点)可用于误差校正,当飞行器到达校正点即能够根据该位置的误差校正类型进行误差校正。校正垂直和水平误差的位置可根据地形在航迹规划前确定。可校正的飞行区域分布位置依赖于地形,无统一规律。若垂直误差、水平误差都能得到及时校正,则飞行器可以按照预定航线飞行,通过若干个校正点进行误差校正后最终到达目的地。
(3) 在出发地A点,飞行器的垂直和水平误差均为0。
(4) 飞行器在垂直误差校正点进行垂直误差校正后,其垂直误差将变为0,水平误差保持不变。
(5) 飞行器在水平误差校正点进行水平误差校正后,其水平误差将变为0,垂直误差保持不变。
(6) 当飞行器的垂直误差不大于 α1α1 个单位,水平误差不大于 α2α2 个单位时才能进行垂直误差校正。
(7) 当飞行器的垂直误差不大于 β1β1 个单位,水平误差不大于 β2β2 个单位时才能进行水平误差校正。
(8) 飞行器在转弯时受到结构和控制系统的限制,无法完成即时转弯(飞行器前进方向无法突然改变),假设飞行器的最小转弯半径为200 m。
围绕在上述轨迹约束条件下,本文为智能飞行器建立航迹规划一般模型和算法。本文针对参考文献 [1] 中的数据,规划分别满足约束条件(1)~(7)和(1)~(8)时,飞行器运行的最优航迹。另外,飞行器的飞行环境可能随时间动态变化,虽然校正点在飞行前已经确定,但飞行器在部分校正点进行误差校正时存在无法达到理想校正的情况(即将某个误差精确校正为0),例如天气等不可控因素导致飞行器到达校正点也无法进行理想的误差校正。若假设飞行器在部分校正点(文献 [1] 中附件1和附件2中F列标记为“1”的数据)能够成功将某个误差校正为0的概率是80%,如果校正失败,则校正后的剩余误差为min (error, 5)个单位(其中error为校正前误差,min为取小函数),本文针对此情况重新规划航迹。
2. 飞行器航迹规划模型
在给定初始点A到终点B条件下,为确保测量飞机从A点通过校正点到达B点的全程距离最小 [2]。设 titi 时刻,飞行器当前位置与可达域校正点的距离为 A(ti)A(ti) [3],结合约束条件,建立飞行器航迹规划模型:
按照本文参数特点,本文采用水平、垂直误差交替校正的方式,为了将飞行器的误差控制在较小的范围内,应当先校正垂直误差,然后校正水平误差,之后依次轮流交替,直至到达终点B。
为求解最优航迹问题,我们设计了两套方案:
方案一:每次选择可达域中最近的校正点,此方案能在某误差得到校正的同时将另一误差控制在最小范围,使得各方向误差距离极限仍有较大空间(记为“误差余量”)能最大程度的保障飞行器抵达终点。但是由于每次选择最短距离前进,过于保守,航迹规划过程中会遇到某点S1可达域为空而无法继续的情况。实际上,前面的规划中若某些点能选择大一点的距离前进,校正相同次数后或能到达S2,而S2可达域非空,可以继续规划航迹,即也许可以避开S1。
方案二:考虑飞行器当前位置到可达域校正点的距离和可达域校正点到达终点的直线距离,计算两距离之和可得多个组合,假设各个校正点为当前位置,计算其是否存在可达域,去除不存在可达域的校正点对应的组合,在剩余组合中取最小组合。该方案属于A*算法的应用,既考虑了当前飞行距离也预估了后续飞行距离,从全局考虑了飞行路径,便于找到较优路径。但是可能遇到可达域为空的情况,此时无法继续规划路径,因而不能抵达终点。
加上约束条件(8)之后,在飞行器遇到障碍物时,并且正处于全局最优路径上的时候,采用局部A*路径规划算法 [4],将障碍物区域表示为一个球体 [5]。则半圆危险度表示为:
当飞行器未遇到障碍物时,危险度为0,飞行器的误差则与到障碍物中心的距离有关,距离越近越危险但误差相对小。(1)式中, RmaxRmax 是障碍物的最大半径, dvdv 是飞行器到障碍物中心的距离。
那么加上约束条件(8)之后,规划模型为:

本文中转弯带来的副作用仅是缩小了校正点的工作域,因此方案一、二的算法规划航迹适用两种情况。
另外,飞行器的飞行环境可能随时间动态变化,虽然校正点在飞行前已经确定,但飞行器在部分校正点进行误差校正时存在无法达到理想校正的情况(即将某个误差精确校正为0)。因此,部分校正点存在校正失效的可能,会增大该方向误差的值,进而减少其误差余量,将影响后续校正点的选择,会改变航迹甚至使得航迹规划失败。因校正失效的概率较低(只有20%),根据不同情况可以用两种方法处理失效的校正:
1) 每次校正后加上概率误差。
2) 极端情况,每次有可能校正失效时都按照校正失效处理,即必然失效。
3. 改进的A*算法
下面我们将在经典的A*算法 [6] - [12] 的基础上,提出了一种改进的A*算法,用于解决本文的飞行器航迹规划问题。
A*算法是一种启发式搜索算法。通过在搜索空间不断评估路径的估价函数值来启发式搜索节点来构造最优路径。通常A*算法的常用估价函数表示为
其中,n为当前节点, f(n)f(n) 是从初始点经由节点为n到目标点的估价函数, g(n)g(n) 是在状态空间中从初始节点到节点n的实际代价, h(n)h(n) 是从节点n到目标节点的估计代价。
A*搜索算法的搜索效率由搜索方向和搜索步长决定。为了提升搜索效率,需要从搜索方向、搜索节点确定改进。路径的优劣则主要依赖于估价函数的设计。所以我们从搜索节点和方向方面改进,结合本文要解决的问题,我们改进了校正点的选择,例如每次选择可达域中最近的校正点,并且本文需要加入水平、垂直的校正,在算法的搜索方向改进中,考虑如果当前校正了水平误差,则水平误差暂时无忧,能最快降低垂直误差的机会就是下一次校正,如此交替进行,这样就 能确保两个误差都尽可能小,所以改进后的算法的设计对极端情况承受能力较强,并将改进的算法的具体步骤设计在下文給出,除非另有说明,否则我们总是在本文中使用算法命名的符号。
第一方面,我们针对所有文献 [1] 中的数据,来分别规划满足约束条件(1)~(7)时,飞行器运行的最优航迹,并综合性考虑以下两个优化目标:
1) 通过算法来预判每个最优路径,使航迹长度尽可能小;
2) 通过算法来使经过校正区域进行校正的次数尽可能少,并讨论分析所用算法的有效性和复杂度。
第二方面,我们针对所有文献 [1] 附件中的数据(参数与第一问的相同),分别规划满足条件(1)~(8)时飞行器的航迹,并综合性考虑以下两个优化目标:
1) 通过算法来预判每个最优路径,使航迹长度尽可能小;
2) 通过算法来使经过校正区域进行校正的次数尽可能少,并讨论分析所用算法的有效性和复杂度。
最后根据一、二两种方案设计出算法1和2,并根据通过软件实现后得出的结果,画出两个方面的两个数据集的航迹规划路径图,见图1~6,将结果(即飞行器从起点出发所经过的误差校正点编号,和校正前的误差)依次填入航迹规划的结果表中,见表1~8,并得出算法的时空复杂度,证明算法是有效可行的,见表9。
算法1
Step1:计算当前点A的可达域;
Step2:若可达域非空,转Step3,否则,标记当前点为失败点,转Step5;
Step3:若终点在可达域中,结束程序,逆序输出轨迹栈元素即可得到航迹规划。否则,转Step4;
Step4:选择可达域中最近的点Aclose作为后继点,将可达域存入可达域栈C中,将上一校正点Apre校正后的水平误差pre_h和垂直误差pre_v存入对应栈,以pre_h和pre_v为基础加上Apre到A点所产生的误差增量来更新对应误差h、v,将后继点加入轨迹栈,标记后继点为当前点,转Step1;
Step5:将轨迹栈中栈顶元素出栈(此元素与当前点一致,均为失败点),再从栈顶出栈一个元素,标记为当前点,将可达域栈栈顶元素出栈,去除可达域中失败点的信息(确保此点不会再有机会选中)之后作为新的可达域,将水平误差栈和垂直误差栈栈顶元素出栈,替换当前水平误差h和垂直误差v,转Step2。
Figure 1. 1 (data 1) track route map
图1. 一(数据1)航迹路径图
Figure 2. 1 (data 2) track route map
图2. 一(数据2)航迹路径图
算法2
Step1:计算当前点A的可达域,若终点是在可达域转Step2;否则转Step3;
Step2:计结束程序,逆序输出轨迹栈元素即可得到航迹规划;
Step3:计计算当前点到达可达域各点的误差,在此误差值下,假设可达域各点Bi为当前点;
Step4:计计算Bi是否存在可达域,将存在可达域的点加入集合P;
Step5:计计算点A到P中各点的距离以及P中各点到终点的距离之和,以上一校正点Apre校正后的水平误差pre_h和垂直误差pre_v为基础加上Apre到A点所产生的误差增量来更新对应误差h、v,取最小距离点作为后继点,将后继点加入轨迹栈,标记后继点为当前点,进入Step1。
Figure 3. 2 (data 1) track route map
图3. 二(数据1)航迹路径图
Figure 4. 2 (data 2) track route map
图4. 二(数据2)航迹路径
第三方面,我们解决飞行器在部分校正点进行误差校正时存在无法达到理想校正的情况,假设飞行器到达该校正点时即可知道在该点处是否能够校正成功,但不论校正成功与否,均不能改变规划路径,因此,部分校正点存在校正失效的可能,会增大该方向误差的值,进而减少其误差余量,将影响后续校正点的选择,会改变航迹甚至使得航迹规划失败。因校正失效的概率较低,只有20%,根据不同情况可以用两种方法处理失效的校正,并设计出算法3和算法4,它是以算法1和算法2为基础调整校正时的误差更新机制。
Figure 5. 3 (data 1) track route map
图5. 三(数据1)航迹路径图
Figure 6. 3 (data 2) track route map
图6. 三(数据2)航迹路径图
| 数据 | 航迹路径 |
| 数据1 | ['A', '503', '200', '136', '80', '237', '278', '375', '172', '340', '277', '501', 'B'] |
| 数据2 | ['A','140', '150', '114', '234', '222', '230', '225', '255', '123', '45', '160', '92', '93', '61', '292', 'B'] |
Table 1. Final track route 1
表1. 最终航迹路径一
| 矫正点编号 | 矫正前垂直误差 | 矫正前水平误差 | 矫正点类型 |
| 0 | 0 | 0 | 出发点A |
| 140 | 5.6558 | 5.6558 | 垂直 |
| 150 | 6.7568 | 12.4126 | 水平 |
| 114 | 15.52 | 8.7632 | 垂直 |
| 234 | 4.5312 | 13.2944 | 水平 |
| 222 | 11.8136 | 7.2823 | 垂直 |
| 230 | 11.16 | 18.4422 | 水平 |
| 225 | 14.9956 | 3.8358 | 垂直 |
| 255 | 7.4652 | 11.3009 | 水平 |
| 123 | 15.9366 | 8.4714 | 垂直 |
| 45 | 10.0062 | 18.4776 | 水平 |
| 160 | 17.4913 | 7.4851 | 垂直 |
| 92 | 5.7762 | 13.2613 | 水平 |
| 93 | 15.2609 | 9.4847 | 垂直 |
| 61 | 9.8342 | 19.3189 | 水平 |
| 292 | 16.3881 | 6.5539 | 垂直 |
| 326 | 6.9605 | 13.5144 | 终点B |
Table 2. Track planning results Table 1: Data 1
表2. 航迹规划结果表一:数据1
| 校正点编号 | 校正前垂直误差 | 校正前水平误差 | 校正点类型 |
| 0 | 0 | 0 | 出发点A |
| 503 | 13.3879 | 13.3879 | 垂直 |
| 200 | 0.8651 | 14.253 | 水平 |
| 136 | 14.2711 | 13.4061 | 垂直 |
| 80 | 4.2867 | 17.6928 | 水平 |
| 237 | 8.9145 | 4.6277 | 垂直 |
| 278 | 17.9422 | 22.57 | 水平 |
| 375 | 23.4841 | 5.5418 | 垂直 |
| 172 | 15.4964 | 21.0382 | 水平 |
| 340 | 21.6449 | 6.1485 | 垂直 |
| 277 | 12.0024 | 18.1509 | 水平 |
| 501 | 20.1663 | 8.164 | 垂直 |
| 612 | 8.49 | 16.654 | 终点B |
Table 3. Track planning results Table 1: Data 2
表3. 航迹规划结果表一:数据2
| 算法 | 数据编号 | 校正点数量(个) | 航迹长度(米) |
| 算法1 | 1 | 31 | 169641 |
| 算法2 | 1 | 11 | 110358 |
| 算法1 | 2 | 31 | 1680639 |
| 算法2 | 2 | 15 | 850848 |
Table 4. Comparison of Algorithms 1 and 2 on Data 1 and 2
表4. 算法1和2在数据1和2上的对比
| 数据 | 航迹路径 |
| 数据1 | ['A', '503', '200', '136', '80', '237', '278', '375', '172', '340', '277', '501', 'B'] |
| 数据2 | ['A','140', '150', '114', '234', '222', '230', '225', '255', '123', '45', '160', '92', '93', '61', '292', 'B'] |
Table 5. Final track route 2
表5. 最终航迹路径二
| 校正点编号 | 校正后垂直误差 | 校正后水平误差 | 校正点类型 |
| 0 | 0 | 0 | 出发点A |
| 503 | 0 | 13.3879 | 垂直 |
| 200 | 0.8651 | 0 | 水平 |
| 136 | 0 | 13.4061 | 垂直 |
| 80 | 4.2867 | 0 | 水平 |
| 237 | 0 | 4.6277 | 垂直 |
| 278 | 17.9422 | 0 | 水平 |
| 375 | 0 | 5.5418 | 垂直 |
| 172 | 15.4964 | 0 | 水平 |
| 340 | 0 | 6.1485 | 垂直 |
| 277 | 12.0024 | 0 | 水平 |
| 501 | 0 | 8.164 | 垂直 |
| 612 | 0 | 0 | 终点B |
Table 6. Track planning results Table 2: Data 1
表6. 航迹规划结果表二:数据1
| 矫正点编号 | 矫正后垂直误差 | 矫正后水平误差 | 矫正点类型 |
| 0 | 0 | 0 | 出发点A |
| 140 | 0 | 5.6558 | 垂直 |
| 150 | 6.7568 | 0 | 水平 |
| 114 | 0 | 8.7632 | 垂直 |
| 234 | 4.5312 | 0 | 水平 |
| 222 | 0 | 7.2823 | 垂直 |
| 230 | 11.1599 | 0 | 水平 |
| 225 | 0 | 3.8358 | 垂直 |
| 255 | 7.4652 | 0 | 水平 |
| 123 | 0 | 8.4714 | 垂直 |
| 45 | 10.0062 | 0 | 水平 |
| 160 | 0 | 7.4851 | 垂直 |
| 92 | 5.7762 | 0 | 水平 |
| 175 | 0 | 8.3641 | 垂直 |
| 279 | 9.6878 | 0 | 水平 |
| 301 | 0 | 4.9531 | 垂直 |
| 61 | 12.3271 | 0 | 水平 |
| 292 | 0 | 6.5539 | 垂直 |
| 326 | 0 | 0 | 终点B |
Table 7. Track planning results Table 2: Data 2
表7. 航迹规划结果表二:数据2
| 数据1 | 数据2 | ||||||
| 矫正点编号 | 矫正后 垂直误差 | 矫正后 水平误差 | 矫正点类型 | 矫正点编号 | 矫正后 垂直误差 | 矫正后 水平误差 | 矫正点类型 |
| 0 | 0 | 0 | 出发点A | 0 | 0 | 0 | 出发点A |
| 503 | 5 | 13.3879 | 垂直 | 157 | 0 | 9.4768 | 垂直 |
| 200 | 5.8651 | 5 | 水平 | 169 | 3.7014 | 0 | 水平 |
| 354 | 5 | 7.23 | 垂直 | 322 | 0 | 4.1481 | 垂直 |
| 80 | 19.8381 | 5 | 水平 | 252 | 3.8718 | 0 | 水平 |
| 237 | 5 | 9.6277 | 垂直 | 266 | 0 | 7.9939 | 垂直 |
| 282 | 18.6817 | 0 | 水平 | 270 | 6.4 | 0 | 水平 |
| 33 | 0 | 2.4699 | 垂直 | 89 | 0 | 7.5508 | 垂直 |
| 11 | 10.9239 | 0 | 水平 | 236 | 10.1274 | 0 | 水平 |
| 403 | 0 | 12.8409 | 垂直 | 132 | 0 | 9.7042 | 垂直 |
| 594 | 11.0291 | 0 | 水平 | 53 | 10.2592 | 0 | 水平 |
| 501 | 0 | 11.1969 | 垂直 | 112 | 0 | 5.2029 | 垂直 |
| 612 | 0 | 0 | 终点B | 268 | 2.1572 | 0 | 水平 |
| 273 | 0 | 5.0481 | 垂直 | ||||
| 103 | 5.2292 | 0 | 水平 | ||||
| 250 | 0 | 5.7711 | 垂直 | ||||
| 243 | 6.9589 | 0 | 水平 | ||||
| 73 | 0 | 3.5428 | 垂直 | ||||
| 82 | 5.7316 | 0 | 水平 | ||||
| 6 | 0 | 7.1847 | 垂直 | ||||
| 249 | 9.0008 | 0 | 水平 | ||||
| 274 | 0 | 2.8407 | 垂直 | ||||
| 51 | 2.6237 | 0 | 水平 | ||||
| 201 | 0 | 7.2799 | 垂直 | ||||
| 12 | 8.7014 | 0 | 水平 | ||||
| 321 | 0 | 7.1906 | 垂直 | ||||
| 279 | 10.3589 | 1 | 水平 | ||||
| 301 | 0 | 5.9531 | 垂直 | ||||
| 38 | 9.8721 | 0 | 水平 | ||||
| 110 | 0 | 3.9265 | 垂直 | ||||
| 61 | 6.843 | 0 | 水平 | ||||
| 292 | 0 | 6.5539 | 垂直 | ||||
| 326 | 0 | 0 | 终点B |
Table 8. Track planning results Table 3: Data 1 and Data 2
表8. 航迹规划结果表三:数据1和数据2
| 算法 | 时间复杂度 | 空间复杂度 |
| 算法1 | N2 | N |
| 算法2 | N3 | N |
Table 9. Space-time complexity of Algorithm 1 - 4
表9. 算法1~4的时空复杂度
算法3
Step1:计算当前点A的可达域;
Step2:若可达域非空,转Step3,否则,标记当前点为失败点,转Step5;
Step3:若终点在可达域中,结束程序,逆序输出轨迹栈元素即可得到航迹规划。否则,转Step4;
Step4:选择可达域中最近的点Aclose作为后继点,将可达域存入可达域栈C中,将上一校正点Apre校正后的水平误差pre_h和垂直误差pre_v存入对应栈,以pre_h和pre_v为基础加上Apre到A点所产生的误差增量来更新对应误差h、v,若后继点为可能失效点,将对应误差加上bia进行二次校正,将后继点加入轨迹栈,标记后继点为当前点,转Step1;
Step5:将轨迹栈中栈顶元素出栈(此元素与当前点一致,均为失败点),再从栈顶出栈一个元素,标记为当前点,将可达域栈栈顶元素出栈,去除可达域中失败点的信息(确保此点不会再有机会选中)之后作为新的可达域,将水平误差栈和垂直误差栈栈顶元素出栈,替换当前水平误差h和垂直误差v,转Step2。
算法4
Step1:计算当前点A的可达域,若终点是在可达域转Step2;否则转Step3;
Step2:结束程序,逆序输出轨迹栈元素即可得到航迹规划;
Step3:计算当前点到达可达域各点的误差,在此误差值下,假设可达域各点Bi为当前点;
Step4:计算Bi是否存在可达域,将存在可达域的点加入集合P;
Step5:计算点A到P中各点的距离以及P中各点到终点的距离之和,以上一校正点Apre校正后的水平误差pre_h和垂直误差pre_v为基础加上Apre到A点所产生的误差增量来更新对应误差h、v,若后继点为可能失效点,将对应误差加上bia进行二次校正,取最小距离点作为后继点,将后继点加入轨迹栈,标记后继点为当前点,进入Step1。
4. 数值结果
本节利用已知数据来验证算法1~4的有效性。我们的数值实验是应用Python和Matlab软件进行计算。
5. 总结
本文使用了一种新的改进的A*算法,算法模型在第一方面中,很好地降低两个误差增长所带来的风险,如当前校正了水平误差,则水平误差暂时无忧,能最快降低垂直误差的机会就是下一次校正,如此交替进行,能确保两个误差都尽可能小,算法的设计对极端情况承受能力较强,得出的路径总长较短,耗费的时间较少,见表1~4。第二方面中,考虑转弯带来的副作用仅是缩小了校正点的工作域,因此还可利用问题1的算法规划航迹,此时需将各个数据对应的参数减小0.63个单位,在问题1算法的基础上规划航迹,减少了工作量,并能得出很好的路径,见表5~7。在第三方面中,考虑到部分校正点存在校正失效的可能,在正常情况和极端情况,每次有可能校正失效时都按照校正失效处理,大大增加了算法的可行性和覆盖性,得出安全可行的路径,见表8。总体来说,算法1~4在空间存在有解航迹时必能保证抵达终点,可以快速找到较优轨迹甚至最优轨迹,两个算法模型优势互补,既能兼顾快速寻优的需求,也能保障有解必达终点的安全性。
审核编辑:汤梓红
 电子发烧友App
电子发烧友App


















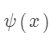














评论