深入理解Linux内核中的算法和数据结构

测试方法准备

由于需要在内核中进行代码测试验证，完整编译安装内核比较耗时耗力。准备采用module形式来验证。

Makefile

obj-m:=linked-list.o

KERNELBUILD:=/lib/modules/$(shell uname -r)/build

default:
        make -C ${KERNELBUILD} M=$(shell pwd) modules
clean:
        rm -rf *.o *.cmd *.ko *.mod.c .tmp_versions

linked-list.c

#include 
#include 
#include 

int linked_list_init(void)
{
    printk("%s\n", __func__);
    return 0;
}

void linked_list_exit(void)
{
    printk("%s\n", __func__);
}

module_init(linked_list_init);
module_exit(linked_list_exit);
MODULE_AUTHOR("Arnold Lu");
MODULE_LICENSE("GPL");
MODULE_DESCRIPTION("Linked list test");

安装module

sudo insmod linked-list.ko

查找安装情况

lsmod | grep linked-list

执行log

<4>[621267.946711] linked_list_init
<4>[621397.154534] linked_list_exit

删除module

sudo rmmod linked-list

链表、双向链表、无锁链表

Linked list, doubly linked list, lock-free linked list.

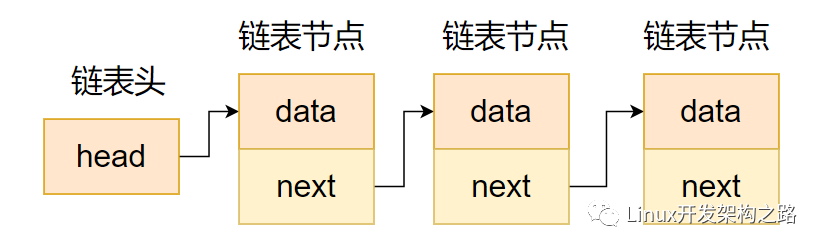
链表是一种常用的组织有序数据的数据结构，它通过指针将一系列数据节点连接成一条数据链，是线性表的一种重要实现方式。相对于数组，链表具有更好的动态性，建立链表时无需预先知道数据总量，可以随机分配空间，可以高效地在链表中的任意位置实时插入或删除数据。链表的开销主要是访问的顺序性和组织链的空间损失。

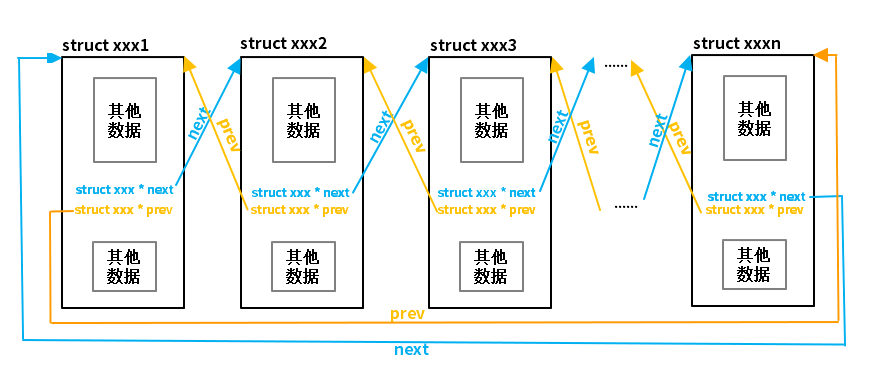
通常链表数据结构至少应包含两个域：数据域和指针域，数据域用于存储数据，指针域用于建立与下一个节点的联系。按照指针域的组织以及各个节点之间的联系形式，链表又可以分为单链表、双链表、循环链表等多种类型.

 

​

 

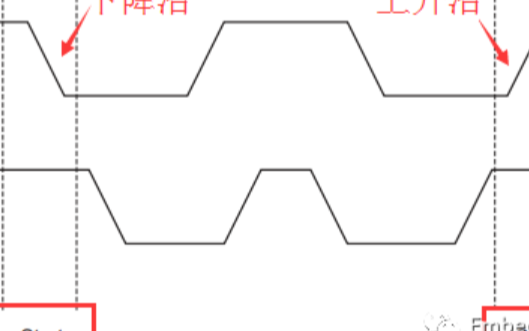
通过设计前驱和后继两个指针域，双链表可以从两个方向遍历，这是它区别于单链表的地方。如果打乱前驱、后继的依赖关系，就可以构成"二叉树"；如果再让首节点的前驱指向链表尾节点、尾节点的后继指向首节点（如图2中虚线部分），就构成了循环链表；如果设计更多的指针域，就可以构成各种复杂的树状数据结构。

 

​
 

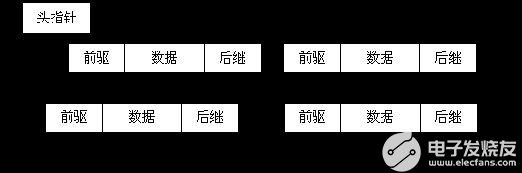
循环链表的特点是尾节点的后继指向首节点。前面已经给出了双循环链表的示意图，它的特点是从任意一个节点出发，沿两个方向的任何一个，都能找到链表中的任意一个数据。如果去掉前驱指针，就是单循环链表。

 

Simple doubly linked list

数据结构：

struct list_head {
    struct list_head *next, *prev;
};

声明和初始化：

static inline void INIT_LIST_HEAD(struct list_head *list)

在表头插入和在表尾插入：

static inline void list_add(struct list_head *new, struct list_head *head)
static inline void list_add_tail(struct list_head *entry, struct list_head *head)

删除，被删除的节点prev、next分别被设为LIST_POISON2、LIST_POISON1，当访问此节点时会引起叶故障。保证不在链表中的节点项不可访问。

static inline void list_del(struct list_head *entry)
static inline void list_del_init(struct list_head *entry) 将entry从链表解下来，重新初始化，就可以访问节点。

将节点从一个链表搬移到另一个链表，根据插入表头和表位分两种：

static inline void list_move(struct list_head *list, struct list_head *head)
static inline void list_move_tail(struct list_head *list, struct list_head *head)

用新节点替换纠结点：

static inline void list_replace(struct list_head *old, struct list_head *new)

将list插入到head：

static inline void list_splice(const struct list_head *list, struct list_head *head)
static inline void list_splice_tail(struct list_head *list, struct list_head *head)
static inline void list_splice_init(struct list_head *list, struct list_head *head) 将list设为空链表
static inline void list_splice_tail_init(struct list_head *list, struct list_head *head) 将list设为空链表

 

​

 

static inline void list_cut_position(struct list_head *list, struct list_head *head, struct list_head *entry)

遍历宏：

list_entry(ptr, type, member)
list_first_entry(ptr, type, member)
list_last_entry(ptr, type, member)
list_next_entry(pos, member)
list_prev_entry(pos, member)
list_for_each(pos, head)
list_for_each_prev(pos, head) 反向操作
list_for_each_safe(pos, n, head) 安全操作
list_for_each_entry(pos, head, member) 遍历链表是获取链表节点
list_for_each_entry_safe(pos, n, head, member) 安全操作
list_for_each_entry_reverse(pos, head, member) 反向操作

判断链表是否为空：

static inline int list_empty(const struct list_head *head)

Doubly linked list with a single pointer list head

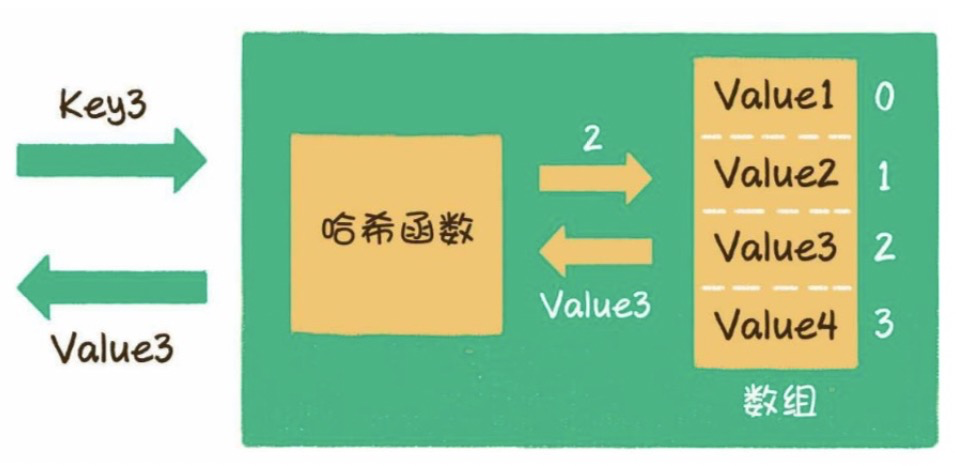
linux内核里边除了著名的list双向循环链表以外，还有一个重要的数据结构，就是哈希链表。哈希链表也在很多重要的地方有所使用，比如linux内核的dentry，进程查询，文件系统等，可以说，弄明白hlist对于理解linux内核具有重要的意义。

struct hlist_head {    struct hlist_node *first; }; struct hlist_node {    struct hlist_node *next, **pprev; };

linux内核的hash链表有两个数据结构组成，一个是hlist_head是hash表的表头，一个是hlist_node是hash标的后续节点。

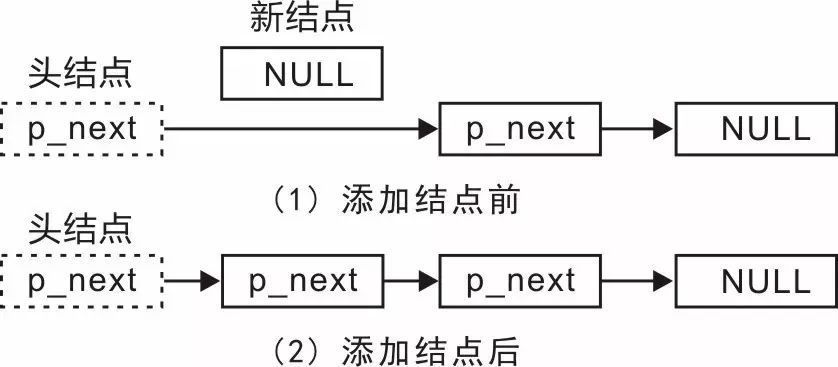
在使用的时候，一般定义一个struct hlist_head xxx[100]数组（100只是一个代表的数字，视具体情况而定），采取哈希函数来将键值与数组的对应的地址联系起来，如果出现冲突的话，就在hlist_head的后边继续添加。 hlist_head的成员first指针指向后续的第一个节点，如果哈希链表是空的话，就为NULL。

为什么hlist_head不弄成双向链表呢，因为为了节约空间，如果一个指针的话，一个哈希数组的空间消耗就会减半。

hlist_node的成员next指向后续的节点的地址，如果为空就是NULL，另一个成员pprev是二级指针，指向前一个节点的next成员的地址，如果前一个成员是hlist_head的话，pprev的值就是前一个的first指针的地址。

#define HLIST_HEAD(name) struct hlist_head name = { .first = NULL } 定义并且初始化。 #define INIT_HLIST_HEAD(ptr) ((ptr)->first = NULL) 在定义之后，需要初始化，不然使用会导致错误。 static inline void INIT_HLIST_NODE(struct hlist_node *h) 初始化node节点 static inline int hlist_empty(const struct hlist_head *h) 判断hash链表是否为空 static inline void hlist_del(struct hlist_node *n) 删除节点，并且将节点next、pprev指针修改为LIST_POSITION1和LIST_POSITION2。 static inline void hlist_del_init(struct hlist_node *n) 此种方法更安全，删除然后再初始化节点。 static inline void hlist_add_head(struct hlist_node *n, struct hlist_head *h) 将节点插入到hash链表的头结点后边。 static inline void hlist_add_before(struct hlist_node *n, struct hlist_node *next) 将一个节点插入到next前面。 static inline void hlist_add_behind(struct hlist_node *n, struct hlist_node *prev) 将一个节点插入到prev后面。 遍历访问节点： hlist_for_each(pos, head) hlist_for_each_safe(pos, n, head) #define hlist_entry(ptr, type, member) container_of(ptr,type,member) hlist_entry_safe(ptr, type, member) hlist_for_each_entry(pos, head, member) hlist_for_each_entry_safe(pos, n, head, member)

Lock-less NULL terminated single linked list

数据结构如下：

struct llist_head {
    struct llist_node *first;
};

struct llist_node {
    struct llist_node *next;
};

 

#define LLIST_HEAD(name) struct llist_head name = LLIST_HEAD_INIT(name) static inline void init_llist_head(struct llist_head *list) llist_entry(ptr, type, member) llist_for_each(pos, node) static inline bool llist_empty(const struct llist_head *head) static inline struct llist_node *llist_next(struct llist_node *node) static inline bool llist_add(struct llist_node *new, struct llist_head *head) bool llist_add_batch(struct llist_node *new_first, struct llist_node *new_last, struct llist_head *head) static inline struct llist_node *llist_del_all(struct llist_head *head) struct llist_node *llist_del_first(struct llist_head *head)

llist_add、llist_add_batch、llist_del_first都是基于cmpxchg原子操作来实现，整个操作是原子的；llist_del_all是基于xchg来实现的。

 

cmpxchg(void* ptr, int old, int new)，如果ptr和old的值一样，则把new写到ptr内存，否则返回ptr的值，整个操作是原子的。在Intel平台下，会用lock cmpxchg来实现，这里的lock个人理解是锁住内存总线，这样如果有另一个线程想访问ptr的内存，就会被block住。

B+树

A relatively simple B+Tree implementation. I have written it as a learning exercise to understand how B+Trees work. Turned out to be useful as well. ... A tricks was used that is not commonly found in textbooks. The lowest values are to the right, not to the left. All used slots within a node are on the left, all unused slots contain NUL values. Most operations simply loop once over all slots and terminate on the first NUL.

B树诞生的背景：

在大规模数据存储中，实现索引查询这样一个实际背景下，树节点存储的元素数量是有限的，这样就会导致二叉树结构由于树的深度过大而造成磁盘I/O读写过于频繁，进而导致查询效率低下。 那么如何减少树的深度，一个基本的想法是采用多叉树结构。 因为磁盘的操作费时费资源，那么如何提高效率，即如何避免频繁的读取呢？根据磁盘查找存取的次数往往由树的高度决定，所以只要通过较好的结构降低树的高度。根据平衡二叉树的启发，自然就想到平衡多叉树结构。

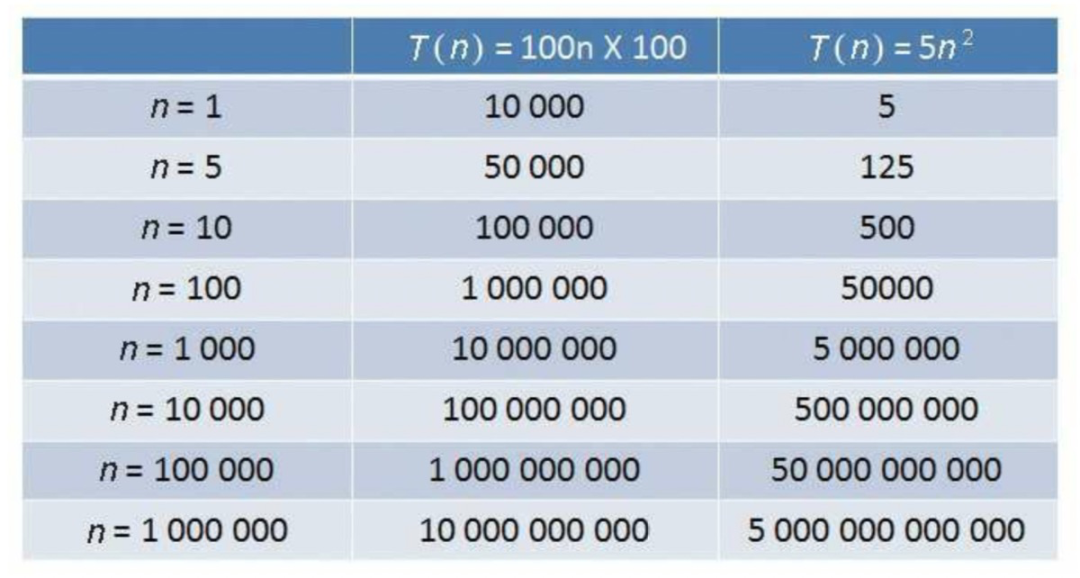
几个算法时间复杂度度量：

O(n) 表示某函数值(未列出)是 n 的常数倍；亦即他们增长的速度相当.称 大O,big O (发音 "欧" 英文字母 O ) 同理:O(logN):是 logN 的常数倍；O(nlogn):是 nlogn 的常数倍

优先排序列表

plist有两个重要结构体struct plist_head和struct plist_node，分别用来表示plist表头和plist节点。

struct plist_head {
    struct list_head node_list;
}；

struct plist_node {
    int prio;
    struct list_head prio_list;
    struct list_head node_list;
};

相关函数：

PLIST_HEAD(head) 初始化plist表头
PLIST_NODE_INIT(node, __prio) 初始化plist节点
static inline void plist_head_init(struct plist_head *head) 初始化plist表头
static inline void plist_node_init(struct plist_node *node, int prio) 初始化plist节点

添加节点、删除节点：

extern void plist_add(struct plist_node *node, struct plist_head *head); 通过plist_add添加到head的node是按照prio优先级由高到低顺序在node_list上排列。
extern void plist_del(struct plist_node *node, struct plist_head *head);
extern void plist_requeue(struct plist_node *node, struct plist_head *head); 是plist_del的优化版本

遍历plist：

plist_for_each(pos, head)

判断head是否为空：

static inline int plist_head_empty(const struct plist_head *head)

判断当前node是否在node_list上：

static inline int plist_node_empty(const struct plist_node *node)

获取前一、后一节点：

plist_next(pos)
plist_prev(pos)

获取首节点、尾节点：

static inline struct plist_node *plist_first(const struct plist_head *head)
static inline struct plist_node *plist_last(const struct plist_head *head)

下面是对plist进行的一些验证：

static dump_list(void)
{
    struct plist_node *node_pos, *first_node, *last_node;
    int i;

    printk(KERN_DEBUG "%s start\n", __func__);
    printk("node_list: ");
    list_for_each_entry(node_pos, &test_head.node_list, node_list) {
        printk("%d ", node_pos->prio);
    }
    printk("\n");

    first_node = plist_first(&test_head);
    last_node = plist_last(&test_head);
    printk("prio_list: %d ", first_node->prio);
    list_for_each_entry(node_pos, &first_node->prio_list, prio_list) {
        printk("%d ", node_pos->prio);
    }
    printk("\n");

#if 0
    for (i = 0; i < ARRAY_SIZE(test_node); i++) {
        if(!plist_node_empty(test_node+i))
            printk(KERN_DEBUG "(test_node+%d)->prio=%d\n", i, (test_node+i)->prio);
    }
#endif
    printk(KERN_DEBUG "MIN(prio)=%d MAX(prio)=%d\n", first_node->prio, last_node->prio);
    printk(KERN_DEBUG "%s end\n", __func__);
}

static int  __init plist_test(void)
{
    int nr_expect = 0, i, loop;
    unsigned int r = local_clock();

    printk(KERN_DEBUG "start plist test\n");
    plist_head_init(&test_head);
    for (i = 0; i < ARRAY_SIZE(test_node); i++)
        plist_node_init(test_node + i, 0);

    for (loop = 0; loop < 10; loop++) {
        r = r * 193939 % 47629;
        i = r % ARRAY_SIZE(test_node);
        if (plist_node_empty(test_node + i)) {
            r = r * 193939 % 47629;
            test_node[i].prio = r % 10;
            plist_add(test_node + i, &test_head);
            nr_expect++;
        } else {
            plist_del(test_node + i, &test_head);
            nr_expect--;
        }
        plist_test_check(nr_expect);
        if (!plist_node_empty(test_node + i)) {
            plist_test_requeue(test_node + i);
            plist_test_check(nr_expect);
        }
    }

    dump_list();

    for (i = 0; i < ARRAY_SIZE(test_node); i++) {
        if (plist_node_empty(test_node + i))
            continue;
        plist_del(test_node + i, &test_head);
        nr_expect--;
        plist_test_check(nr_expect);
    }

    printk(KERN_DEBUG "end plist test\n");
    return 0;
}

通过初始化不超过10个node节点，优先级为0-9。然后查看node_list和prio_list两链表的节点情况：

[22050.404475] start plist test [22050.404481] dump_list start [22050.404482] node_list: 0 0 1 1 2 6 8 8 9 9 [22050.404486] prio_list: 0 1 2 6 8 9 [22050.404488] MIN(prio)=0 MAX(prio)=9 [22050.404489] dump_list end [22050.404491] end plist test [22050.947810] start plist test [22050.947816] dump_list start [22050.947817] node_list: 0 1 1 2 2 3 3 3 8 8 [22050.947820] prio_list: 0 1 2 3 8 [22050.947822] MIN(prio)=0 MAX(prio)=8 [22050.947823] dump_list end [22050.947825] end plist test [22051.491245] start plist test [22051.491254] dump_list start [22051.491256] node_list: 0 1 2 3 3 3 6 9 9 9 [22051.491262] prio_list: 0 1 2 3 6 9 [22051.491266] MIN(prio)=0 MAX(prio)=9 [22051.491267] dump_list end [22051.491271] end plist test

可以看出node_list上的节点按照优先级由高到低排序，优先级可能会重复；在prio_list上是不同优先级的节点。如下所示：

* pl:prio_list (only for plist_node) * nl:node_list *HEAD| NODE(S) * | * ||------------------------------------| * ||->|pl|<->|pl|<--------------->|pl|<-| * | |10| |21| |21| |21| |40| (prio) * | | | | | | | | | | | * | | | | | | | | | | | * | ->|nl|<->|nl|<->|nl|<->|nl|<->|nl|<->|nl|<-| * |-------------------------------------------------|

红黑树

Red-Black treesareusedfor scheduling, virtual memory management, to track file descriptors and directory entries,etc.


审核编辑：汤梓红