摘要:HTTP Live Streaming(缩写是HLS)是一个由苹果公司提出的基于HTTP的流媒体网络传输协议。今天主要以HLS协议为中心讲述它的一些原理。
HLS协议简介
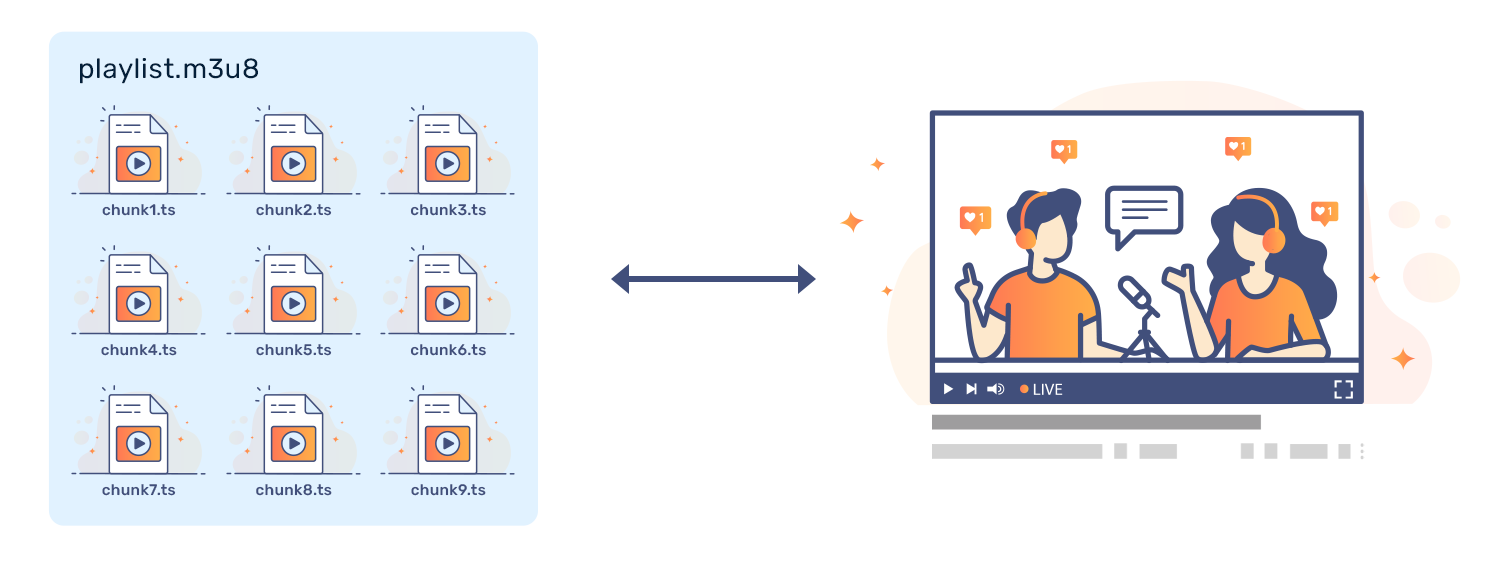
HTTP Live Streaming(缩写是HLS)是一个由苹果公司提出的基于HTTP的流媒体网络传输协议。是苹果公司QuickTime X和iPhone软件系统的一部分。它的工作原理是把整个流分成一个个小的基于HTTP的文件来下载,每次只下载一些。当媒体流正在播放时,客户端可以选择从许多不同的备用源中以不同的速率下载同样的资源,允许流媒体会话适应不同的数据速率。在开始一个流媒体会话时,客户端会下载一个包含元数据的extended M3U (m3u8)playlist文件,用于寻找可用的媒体流。
HLS只请求基本的HTTP报文,与实时传输协议(RTP)不同,HLS可以穿过任何允许HTTP数据通过的防火墙或者代理服务器。它也很容易使用内容分发网络来传输媒体流。
苹果公司把HLS协议作为一个互联网草案(逐步提交),在第一阶段中已作为一个非正式的标准提交到IETF。但是,即使苹果偶尔地提交一些小的更新,IETF却没有关于制定此标准的有关进一步的动作。
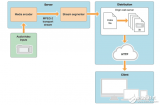
HLS整体架构
上面是HLS整体架构图,可以看出,总共有三个部分:Server,CDN,Client.
HLS协议规定要求
1.视频的封装格式是TS。
2.视频的编码格式为H264,音频编码格式为MP3、AAC或者AC-3。
3.除了TS视频文件本身,还定义了用来控制播放的m3u8文件(文本文件)。
为什么苹果要提出HLS这个协议,其实他的主要是为了解决RTMP协议存在的一些问题。比如RTMP协议不使用标准的HTTP接口传输数据,所以在一些特殊的网络环境下可能被防火墙屏蔽掉。但是HLS由于使用的HTTP协议传输数据,不会遇到被防火墙屏蔽的情况(该不会有防火墙连80接口都不放过吧)。
另外于负载,RTMP是一种有状态协议,很难对视频服务器进行平滑扩展,因为需要为每一个播放视频流的客户端维护状态。而HLS基于无状态协议(HTTP),客户端只是按照顺序使用下载存储在服务器的普通TS文件,做负责均衡如同普通的HTTP文件服务器的负载均衡一样简单。
另外HLS协议本身实现了码率自适应,不同带宽的设备可以自动切换到最适合自己码率的视频播放。其实HLS最大的优势就是他的亲爹是苹果。苹果在自家的IOS设备上只提供对HLS的原生支持,并且放弃了flash。Android也迫于平果的“淫威”原生支持了HLS。这样一来flv,rtmp这些Adobe的视频方案要想在移动设备上播放需要额外下点功夫。当然flash对移动设备造成很大的性能压力确实也是自身的问题。
但HLS也有一些无法跨越的坑,比如采用HLS协议直播的视频延迟时间无法下到10秒以下,而RTMP协议的延迟最低可以到3、4秒左右。所以说对直播延迟比较敏感的服务请慎用HLS。
HLS的请求流程:
1 http请求m3u8 的 url。
2 服务端返回一个m3u8的播放列表,这个播放列表是实时更新的,一般一次给出5段数据的url。
3 客户端解析m3u8的播放列表,再按序请求每一段的url,获取ts数据流。
RSA实现细节
密钥生成
首先要使用概率算法来验证随机产生的大的整数是否质数,这样的算法比较快而且可以消除掉大多数非质数。假如有一个数通过了这个测试的话,那么要使用一个精确的测试来保证它的确是一个质数。
除此之外这样找到的p和q还要满足一定的要求,首先它们不能太靠近,此外p-1或q-1的因子不能太小,否则的话N也可以被很快地分解。
此外寻找质数的算法不能给攻击者任何信息,这些质数是怎样找到的,尤其产生随机数的软件必须非常好。要求是随机和不可预测。这两个要求并不相同。一个随机过程可能可以产生一个不相关的数的系列,但假如有人能够预测出(或部分地预测出)这个系列的话,那么它就已经不可靠了。比如有一些非常好的随机数算法,但它们都已经被发表,因此它们不能被使用,因为假如一个攻击者可以猜出p和q一半的位的话,那么他们就已经可以轻而易举地推算出另一半。
此外密钥d必须足够大,1990年有人证明假如p大于q而小于2q(这是一个很经常的情况)而,那么从N和e可以很有效地推算出d。此外e = 2永远不应该被使用。
运算速度
由于进行的都是大数计算,使得RSA最快的情况也比DES慢上好几倍,无论是软件还是硬件实现。速度一直是RSA的缺陷。一般来说只用于少量数据加密。RSA的速度比对应同样安全级别的对称密码算法要慢1000倍左右。
比起DES和其它对称算法来说,RSA要慢得多。实际上Bob一般使用一种对称算法来加密他的信息,然后用RSA来加密他的比较短的对称密码,然后将用RSA加密的对称密码和用对称算法加密的消息送给Alice。
这样一来对随机数的要求就更高了,尤其对产生对称密码的要求非常高,因为否则的话可以越过RSA来直接攻击对称密码。
密钥分配
和其它加密过程一样,对RSA来说分配公钥的过程是非常重要的。分配公钥的过程必须能够抵挡一个从中取代的攻击。假设Eve交给Bob一个公钥,并使Bob相信这是Alice的公钥,并且她可以截下Alice和Bob之间的信息传递,那么她可以将她自己的公钥传给Bob,Bob以为这是Alice的公钥。Eve可以将所有Bob传递给Alice的消息截下来,将这个消息用她自己的密钥解密,读这个消息,然后将这个消息再用Alice的公钥加密后传给Alice。理论上Alice和Bob都不会发现Eve在偷听他们的消息。今天人们一般用数字认证来防止这样的攻击。
RSA缺点
1)产生密钥很麻烦,受到素数产生技术的限制,因而难以做到一次一密。
2)安全性,RSA的安全性依赖于大数的因子分解,但并没有从理论上证明破译RSA的难度与大数分解难度等价,而且密码学界多数人士倾向于因子分解不是NP问题。
3)速度太慢,由于RSA 的分组长度太大,为保证安全性,n 至少也要 600 bits以上,使运算代价很高,尤其是速度较慢,较对称密码算法慢几个数量级;且随着大数分解技术的发展,这个长度还在增加,不利于数据格式的标准化。
RSA的安全性
首先,我们来探讨为什么RSA密码难于破解?
在RSA密码应用中,公钥KU是被公开的,即e和n的数值可以被第三方窃听者得到。破解RSA密码的问题就是从已知的e和n的数值(n等于pq),想法求出d的数值,这样就可以得到私钥来破解密文。从上文中的公式:d ≡e-1 (mod((p-1)(q-1)))或de≡1 (mod((p-1)(q-1))) 我们可以看出。密码破解的实质问题是:从Pq的数值,去求出(p-1)和(q-1)。换句话说,只要求出p和q的值,我们就能求出d的值而得到私钥。
当p和q是一个大素数的时候,从它们的积pq去分解因子p和q,这是一个公认的数学难题。比如当pq大到1024位时,迄今为止还没有人能够利用任何计算工具去完成分解因子的任务。因此,RSA从提出到现在已近二十年,经历了各种攻击的考验,逐渐为人们接受,普遍认为是目前最优秀的公钥方案之一。
然而,虽然RSA的安全性依赖于大数的因子分解,但并没有从理论上证明破译RSA的难度与大数分解难度等价。即RSA的重大缺陷是无法从理论上把握它的保密性能如何。
此外,RSA的缺点还有:A)产生密钥很麻烦,受到素数产生技术的限制,因而难以做到一次一密。B)分组长度太大,为保证安全性,n 至少也要 600 bits 以上,使运算代价很高,尤其是速度较慢,较对称密码算法慢几个数量级;且随着大数分解技术的发展,这个长度还在增加,不利于数据格式的标准化。因此,使用RSA只能加密少量数据,大量的数据加密还要靠对称密码算法。
实例描述
在这篇科普小文章里,不可能对RSA算法的正确性作严格的数学证明,但我们可以通过一个简单的例子来理解RSA的工作原理。为了便于计算。在以下实例中只选取小数值的素数p,q,以及e,假设用户A需要将明文“key”通过RSA加密后传递给用户B,过程如下:
(1)设计公私密钥(e,n)和(d,n)。
令p=3,q=11,得出n=p×q=3×11=33;f(n)=(p-1)(q-1)=2×10=20;取e=3,(3与20互质)则e×d≡1 mod f(n),即3×d≡1 mod 20。
d怎样取值呢?可以用试算的办法来寻找。试算结果见下表:
通过试算我们找到,当d=7时,e×d≡1 mod f(n)同余等式成立。因此,可令d=7。从而我们可以设计出一对公私密钥,加密密钥(公钥)为:KU =(e,n)=(3,33),解密密钥(私钥)为:KR =(d,n)=(7,33)。
(2)英文数字化。
将明文信息数字化,并将每块两个数字分组。假定明文英文字母编码表为按字母顺序排列数值,即:
则得到分组后的key的明文信息为:11,05,25。
(3)明文加密
用户加密密钥(3,33) 将数字化明文分组信息加密成密文。由C≡Me(mod n)得:

因此,得到相应的密文信息为:11,31,16。
(4)密文解密。
用户B收到密文,若将其解密,只需要计算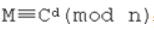 ,即:
,即:
用户B得到明文信息为:11,05,25。根据上面的编码表将其转换为英文,我们又得到了恢复后的原文“key”。
你看,它的原理就可以这么简单地解释!
当然,实际运用要比这复杂得多,由于RSA算法的公钥私钥的长度(模长度)要到1024位甚至2048位才能保证安全,因此,p、q、e的选取、公钥私钥的生成,加密解密模指数运算都有一定的计算程序,需要仰仗计算机高速完成。
 电子发烧友App
电子发烧友App




























评论