FPGA实现ISP常见2D去噪的方法

一. 2D 去噪介绍

ISP中通常包括对图像的去噪，英文名称为Image Denoising。是指的对数字图像中的噪声进行消除或减少的过程。2D去噪指的是对单帧图像进行帧内降噪处理，而3D去噪则需要关联前后帧。本文仅介绍几种常见的基于滤波器的方法的2D去噪：均值滤波、高斯滤波、中值滤波。

二. 均值滤波

均值滤波是一种典型的线性滤波算法。原理很简单，以当前处理像素为中心，取n x n大小的图像矩阵，求出该矩阵内的像素的均值替代该像素，如此遍历整个图像，即可完成整幅图像的均值滤波。

以5x5的滤波矩阵为例，算法示意图如图2-1所示。

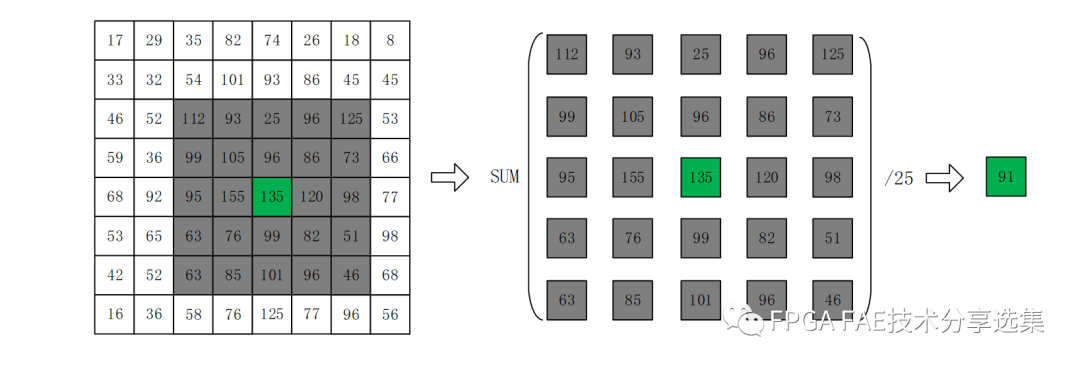
图2-1 均值滤波原理示意图

均值滤波的FPGA实现框图如图2-2所示，以行方式输入的图像信号通过line_cache处理后,以5行的形式输出，输送至avg_filter_process进行5x5的滤波处理。以图像大小1080P,像素深度为12bit灰度为例，用于缓存的RAM大小为1920x48（深度1920，宽度12x4）。

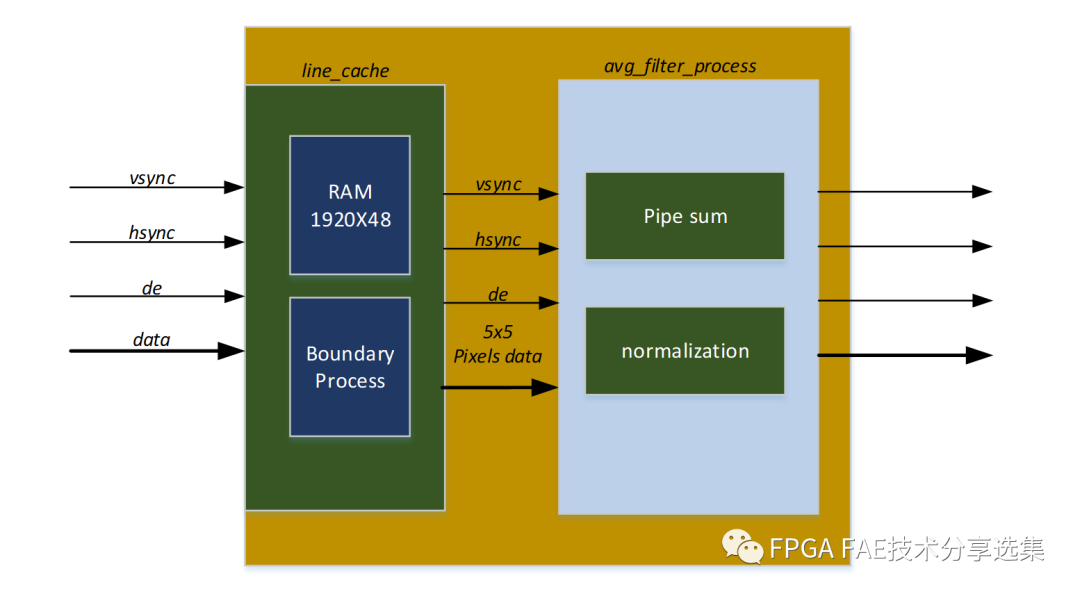
图2-2 均值滤波FPGA实现框图

line_cache每进来一行,会将缓存在RAM_1920x48中的前4行的像素逐个取出,加上新输入的一行图像,组成一个个5x5的矩阵,并组成新的4行数据(48bit)写入RAM_1920x48中,准备给下一行使用。此过程中需要对图像上下左右的边界进行边界处理，即输入图像大小为1924x1084。然后对5x5的矩阵的矩阵相加再除25。除操作通常转换为近似的乘操作，如该代码中会乘以2641（1/25*2^16），再将结果右移16位。

仿真结果见图2-3、图2-4。

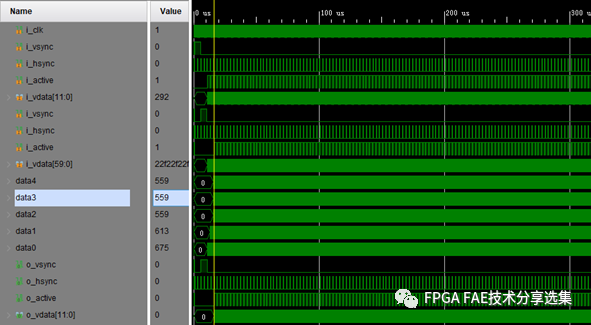
图2-3 均值滤波仿真图1

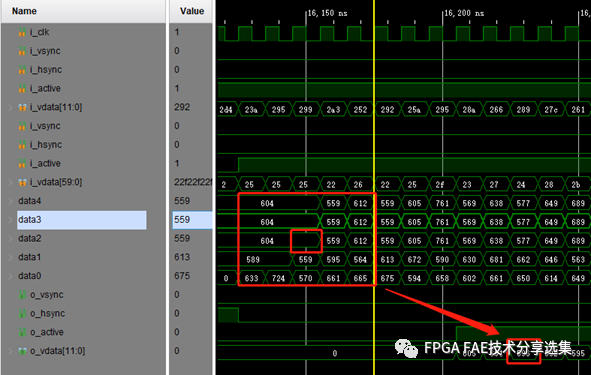
图2-4 均值滤波仿真图2

效果对比图如图2-5，左边为原图，右边为均值滤波后的结果。

图2-5 均值滤波效果对比图

基于5x5的均值滤波会引入两行的延时。基于Xilinx 7A50T的资源占用如图2-6所示。

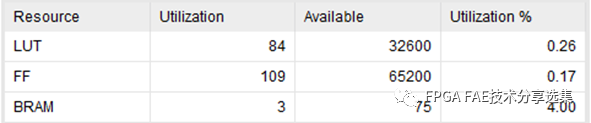
图2-6 资源占用情况

三. 高斯滤波

高斯滤波就是对整个图像进行加权平均的过程，每一个像素点的值，都由其本身和邻域内的其他像素值经过加权平均后得到。高斯滤波的具体操作是：用一个模板（或称卷积、掩模）扫描图像中的每一个像素，用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值。

高斯滤波的公式为：f(x)=aexp [-(x-m)^2/2σ^2]

其中,a是常数,m是均值,σ是标准差。

本文介绍基于Xilinx FPGA实现的5x5的滤波，处理的图像是bayer图像，并且对bayer图像中的R、Gr、B、Gb四个通道分开进行处理。以bayer图像中的一个像素进行高斯滤波为例，处理过程：首先以目标像素为中心取出一个9x9的像素阵列，再在该9x9像素阵列的基础上取出一个5x5的像素阵列，然后将像素阵列中的像素值与对应的滤波系数相乘，再将所有值相加，最后将所得的值除以滤波系数之和，相除所得的值就是高斯滤波的结果。

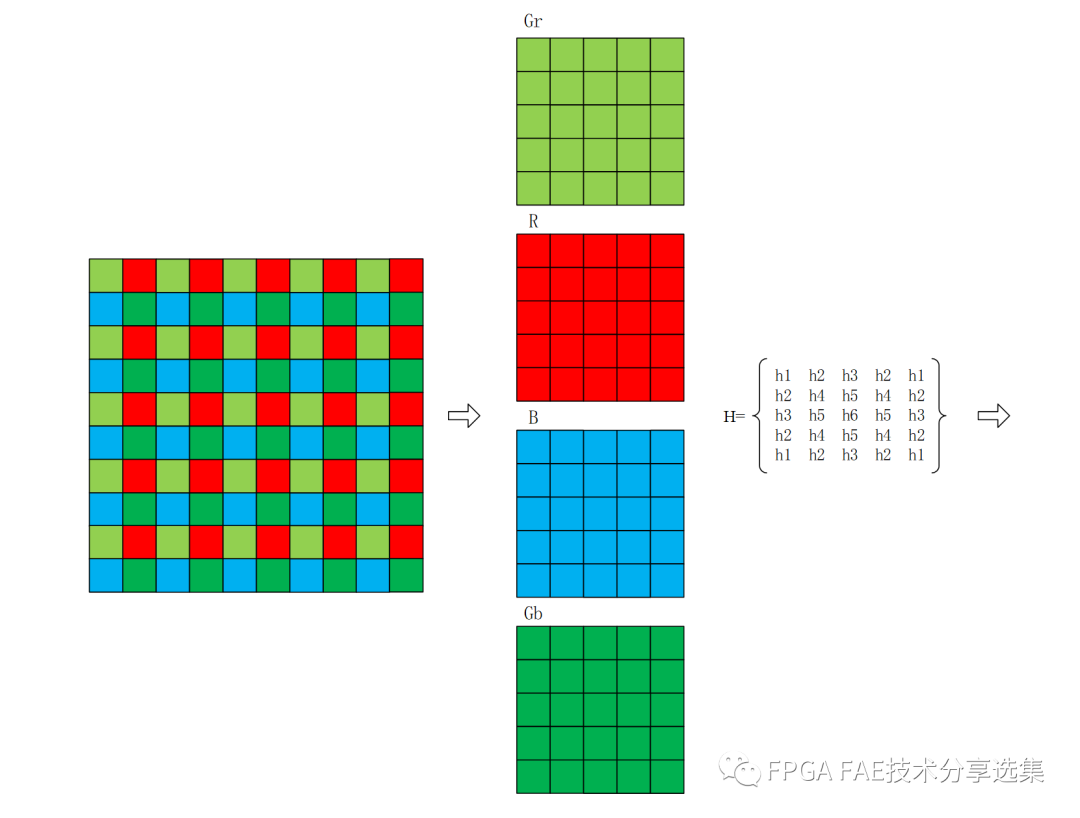
图3-1 高斯滤波原理示意图

其中高斯滤波的滤波系数H由标准差σ确定。本文中使用的滤波系数如图3-2所示。

图3-2 高斯滤波的滤波系数

高斯滤波的FPGA实现框图如图3-3所示，实现方式与均值滤波类似。由于是基于Bayer图像，需要先将Bayer图像的通道分离，分别进行处理。另外5x5的均值滤波可以理解为滤波系数均为1的高斯滤波，其他处理过程一致。

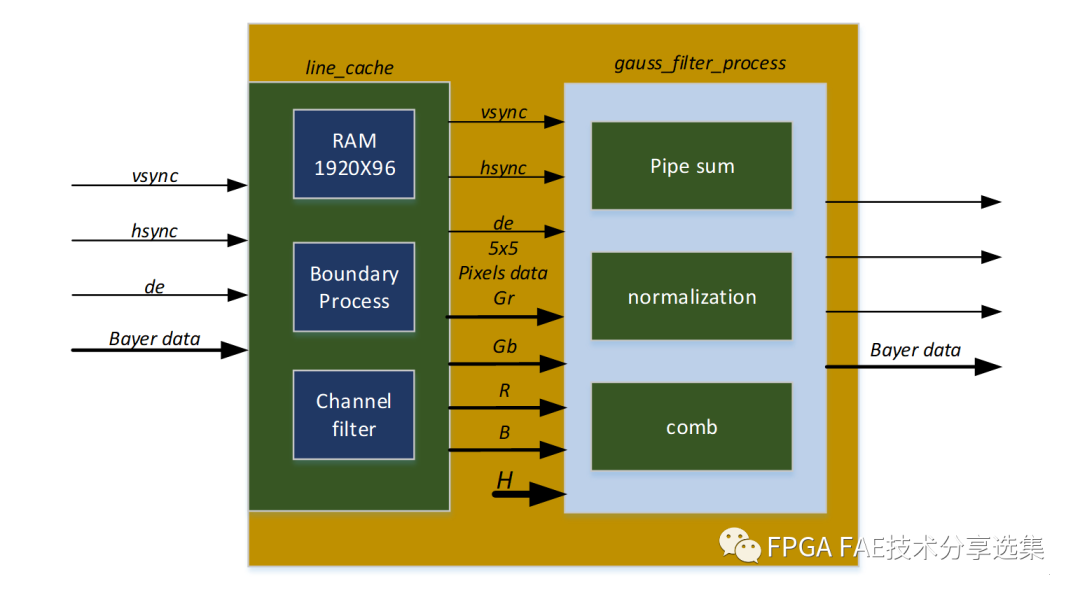
图3-3 高斯滤波FPGA实现框图

line_cache的处理与均值滤波类似，只是缓存行数由4行增加到了8行。对5x5的矩阵数据均乘以一个系数H，再将所有值相加，最后将所得的值除以滤波系数之和，相除所得的值就是高斯滤波的结果。Pipe line的处理方式如图3-4所示。

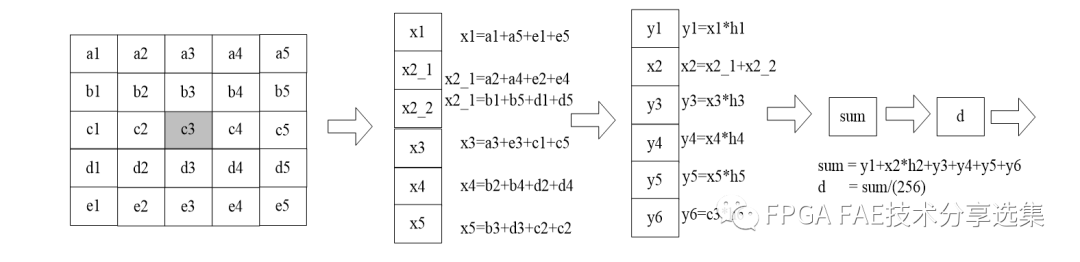
图3-4 高斯滤波FPGA处理流程

仿真波形如图3-5、图3-6。

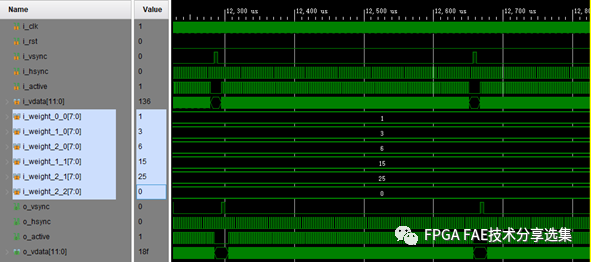
图3-5 高斯滤波仿真图1

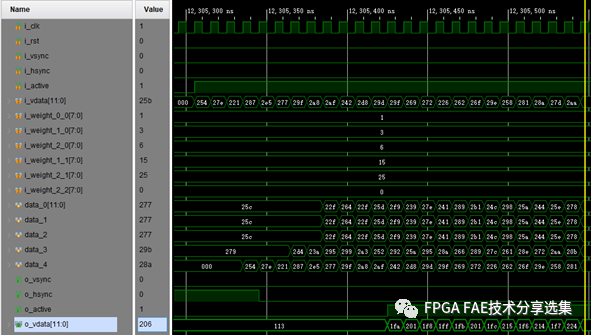
图3-6 高斯滤波仿真图2

效果对比如图3-7，左边为原图，右边为高斯滤波后的结果。

图3-7 高斯滤波效果对比图

高斯滤波与均值滤波类似，总体是对图像进行一个只跟距离有关的抹平。因此对边缘细节没有保留，效果也差别不大。

基于5x5的均值滤波会引入四行的延时。基于Xilinx 7A50T的资源占用如图所示。

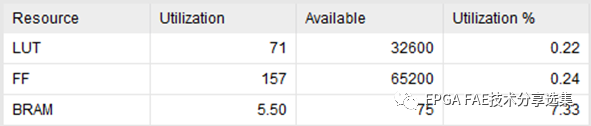
图3-8 资源占用情况

四. 中值滤波

中值滤波是一种非线性滤波算法。原理也很简单，以当前处理像素为中心，取n x n大小的图像矩阵，将该矩阵内的像素值进行排序，将值大小排列在最中间的像素替换该点。如此遍历整个图像，即可完成整幅图像的中值滤波。

以3x3的滤波矩阵为例，算法示意图如图4-1所示。

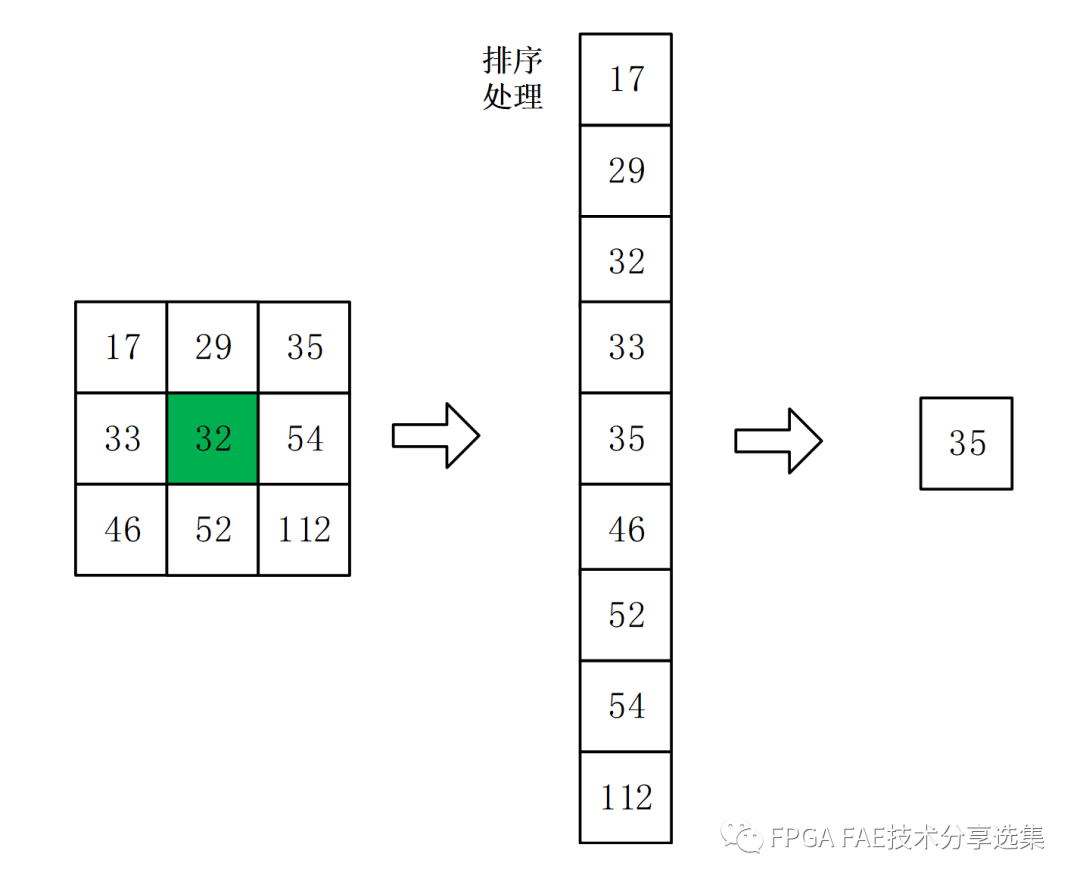
图4-1 中值滤波原理示意图

中值滤波的FPGA实现框图如图4-2所示。以图像大小1080P,像素深度为8bit灰度为例，用于缓存的RAM大小为1920x16（深度1920，宽度8x2）。

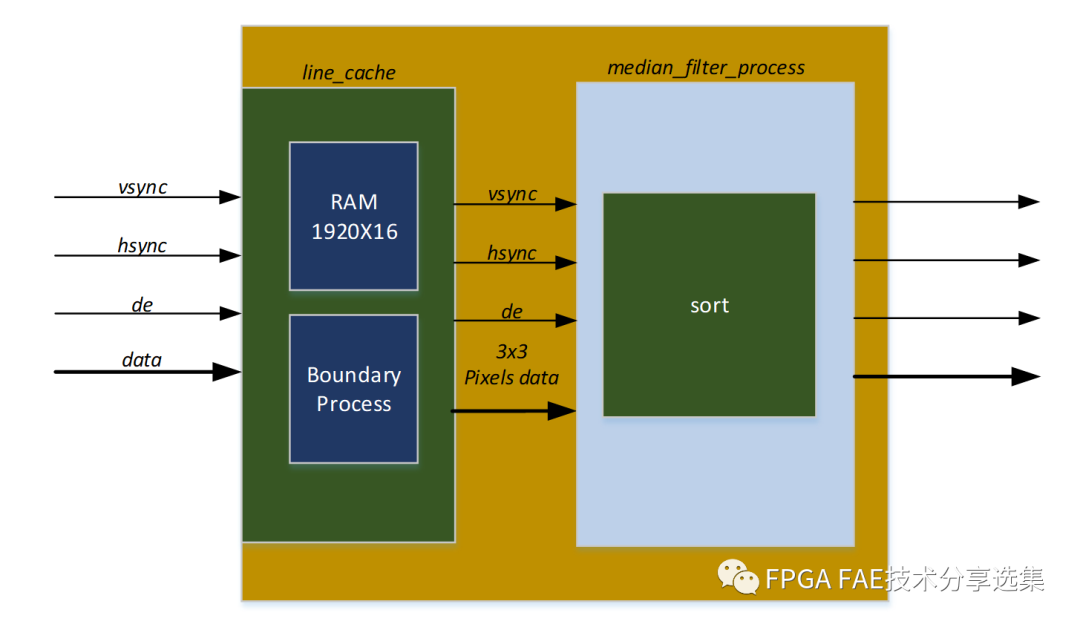
图4-2 中值滤波FPGA实现框图

line_cache的处理与均值滤波类似，只是缓存行数由4行减少到了2行。对输出的3x3矩阵内的9个数进行排序，输出中间值即可。

仿真波形如图4-3、图4-4。

图4-3 中值滤波仿真图1

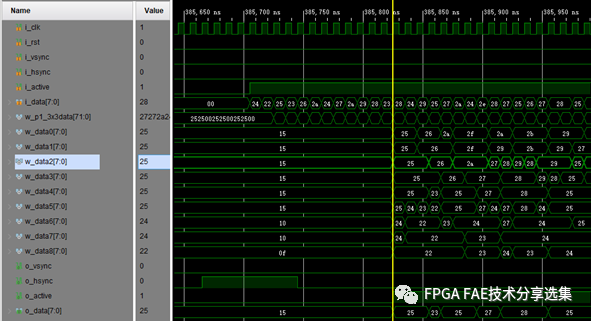
图4-4 中值滤波仿真图2

效果对比如图4-5所示，左边为原图，右边为中值滤波后的结果。

图4-5 中值滤波效果对比图

中值滤波原理决定了其能较好地消除孤立的噪声点而不会对图像造成较大的抹平模糊（相较于均值滤波和高斯滤波）。因此对边缘细节保留较好。

基于3x3的均值滤波会引入一行的延时。基于Xilinx 7A50T的资源占用如图所示。

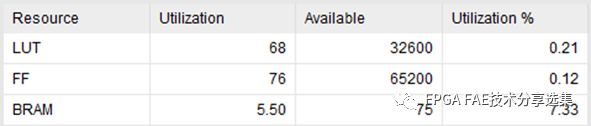
图4-6 资源占用情况

五. 延申

以上几种2D去噪算法均为最基础的去噪处理，实际应用中，不一定能满足我们的应用需求。因此，基于上述几种滤波器，通常还有一些改进型。如：

A. 双边滤波器: 双边滤波器实际上是在高斯滤波器的基础上引入像素差值作为H滤波器系数的参考，权重系数动态变化，使得滤波器在滤除噪声的同时也能保留图像的边缘信息。

B. 自适应的中值滤波器: 中值滤波器的开窗大小可以应对不同的噪声密度，但是窗口越大，图像的失真也会越大。因此增加一个对噪声密度进行判断的模块从而指导中值滤波器动态地变化滤波开窗大小，就能同时兼顾去噪和保留图像的细节。





审核编辑：刘清