在本文中,我们将简要介绍不同类型的滤波器,然后学习如何实现移动平均滤波器并使用CIC架构对其进行优化。
在许多设计中,滤波非常重要。它为我们提供了一个机会,可以提取隐藏在大量噪声下的所需信号。我们还可以通过在某些频率上滤波其输出来确定系统的非线性。
让我们首先讨论滤波器类型之间的一些差异。
理论
滤波器类型
滤波器可根据其带类别分为五组中的一组。每个人的能力都以他们的名义暗示。例如,低通滤波器是一种通过低频输入并阻止高频输入等的滤波器。
五种类型是:
低通带通带阻高通全部通过滤波器也有不同的形状。例如,它们的通带上可能有纹波,或者它们可能具有平坦的过渡带等。
滤波器形状
滤波器通常可按形状分类如下:
贝塞尔:与其他人相比最平坦的群体延迟Butterworth**: 设计为在通带内具有最平坦的频率响应; 也被称为“最大平坦” Chebyshev :设计为在理想滤波器和实际滤波器之间具有最小误差; 可以分为两种类型:通带中具有纹波的那些以及阻带中具有纹波的那些Elliptic :在pass和stop波段都有波纹,但是它们在pass和stop band之间有最快的过渡选择滤波器的形状取决于所需的规格。例如,我们可能需要输出信号幅度尽可能精确地跟随通带中的输入信号幅度。在这种情况下,我们应该使用巴特沃斯滤波器,即使它会给我们更多的过渡带。**
另一方面,我们可能希望输出信号频率精确地跟随输入信号的线性相位响应,因此我们应该选择贝塞尔滤波器。如果我们需要使用尽可能少的组件并且具有与其他滤波器相同的顺序和转换速度,则Elliptic或Chebyshev滤波器可以工作,但是我们在通过或阻止频带中会产生纹波。
模拟和数字滤波器
在另一方面,滤波器可以以两种方式构造:数字和模拟。
在模拟电路中,无源滤波器是电感器,电容器或电阻器的阶梯。有源模拟滤波器可以是利用放大器或谐振器的结构。它们的值可以通过使用已经为设计模拟滤波器而创建的表格或应用程序来确定。
可以使用IIR和FIR两种方法创建数字滤波器。IIR(无限脉冲响应)滤波器是滤波器的类型,其中输出取决于输入和先前的输出。
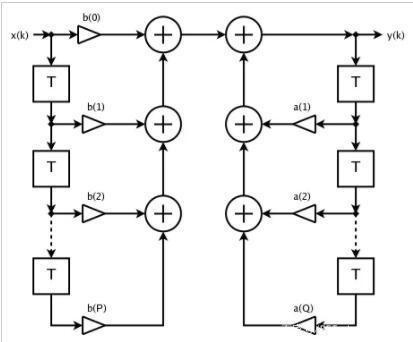
图1. IIR滤波器。图片由Mark Wilde提供
**数字滤波器的另一种滤波器实现是FIR(有限脉冲响应)。这些不使用反馈,它们的输出仅与当前和先前的输入相关。关于稳定性,FIR滤波器总是稳定的,**因为它们的输出仅与输入有关。另一方面,他们需要更高的订单以满足与IIR相同的规格。
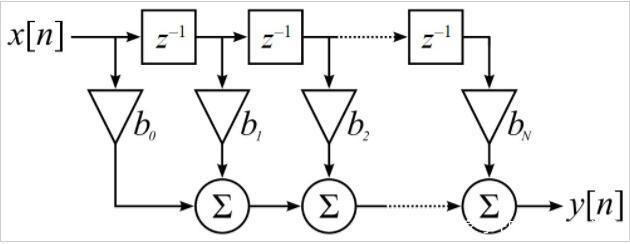
图2. FIR滤波器图片由Jonathan Blancha
移动平均线
移动平均线是一个滤波器,用于平均先前输入的N个点并使用它们输出。
**[ n ] = 1Σi = 0Xn - 我y[n]=1N∑i=0Nxni**
如您所见,移动平均滤波器是N个系数为 的FIR滤波器。 一些不同n的移动平均滤波器的频率响应如图3所示。
1N1N
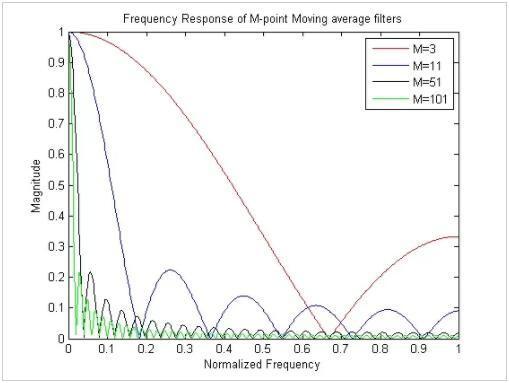
图3.移动平均线的频率响应
移动平均(MA)滤波器的脉冲响应在不在0到N内的点中为零。
**h [ n ] = 1Σk = 0- 1δ[ n - k ]h[n]=1N∑k=0N1δ[nk]**
因此,MA滤波器的频率响应是:
H(ω)=1NejωN/2ejω/2j2sin(ωN2)j2sin(ω2)=1NejωN/2ejω/2sin(ωN2)sin(ω2)H(ω)=1NejωN/2ejω/2j2sin(ωN2)j2sin(ω2)=1NejωN/2ejω/2sin(ωN2)sin(ω2)
截止频率可以估算为:
Fc o= 0.4429472- 1- - - - - - √Fco=0.442947N21
根据这些公式,截止频率仅与N有关。随着N增加,截止频率降低但是花费时间。我们需要等待第N个周期才能得到正确的结果,所以N越大,我们需要更多的时间。随着滤波器越来越清晰,其输出需要达到稳定状态的时间也会增加。
所需设计的滤波和实现是FPGA设计中的主题。需要学习很多东西来设计合适的滤波器,然后在FPGA上以最少的资源使用或最快的速度实现它。
在本文中,我们将尝试实现N点移动平均滤波器。我们假设N是一个参数,可以在实施之前通过Xilinx ISE等CAD工具进行更改。
正如我们在图2中看到的,FIR滤波器可以通过延迟链实现,其长度为N,即FIR阶,将系数乘以延迟线的乘法器,以及一些加法器,用于增加乘法器的结果。这种架构需要许多乘法器和加法器,这些乘法器和加法器在FPGA中受到限制,具体取决于您使用的FPGA(尽管即使是功能最强大的FPGA也是有限的)。
设计FIR过滤器需要一些研究来减少这些资源,因为在设计的每个阶段,任何FPGA都需要减少。然而,我们不会谈论这个话题,相反,我们将用另一个技巧来设计我们的移动平均滤波器。在移动平均滤波器中,所有系数都是1n。如果我们想实现我们的滤波器,如图2,我们应该做一个点击延迟线和存储n最后的输入,然后乘以1n,最后总结结果。但是,我们可以将最后一个输入存储在一个FIFO中,然后将它们相加,然后在每个循环中乘以1/n。用这种方法,我们只需要一个n乘数。
代码说明
首先,我们有N,它是输入点的数量,作为可以调整的参数。我们将添加这N个点以产生输出。
我们还假设我们的输入是28位格式,我们希望输出格式相同。在处理添加N点时,我们可能会面临一点点增长。添加两个28位点会产生28位输出和一个溢出位。因此,为了增加N 28位点,我们需要一个(log2(N)+28)位输出。
假设所有N个点都相同,并且添加它们就像将N乘以其中一个。这就是为什么我们实现一个“log2”函数,它只是简单地计算其输入的对数。通过知道N的对数,我们可以设置输出长度。请注意,log2不是可综合的方法,只能用于Xilinx ISE(即,Xilinx ISE计算log2,然后将结果用于其余的实现)。
“log2”函数如下代码所示:
**function integer log2(input integer v); begin log2=0; while(v>>log2) log2=log2+1; end endfunction**
现在我们设置输入和输出长度,我们需要创建一个存储N个前一个和当前输入的抽头线。以下代码将起到作用:
genvar i;
generate
for (i = 0; i < N-1 ; i = i + 1) begin: gd
always @(posedge clock_in) begin
if(reset==1'b1)
begin
data[i+1]<=0;
end
else
begin
data[i+1] <= data[i];
end
end
end
endgenerate
最后,我们需要一个加法器来汇总存储在FIFO中的所有数据。这个阶段有点棘手。如果我们想在每个时钟周期都有输出,我们需要制作一个组合电路,逐步将数据添加到FIFO中。下面显示的代码将执行此操作:
genvar c;
generate
assign summation_steps[0] = data[0] + data[1];
for (c = 0; c < N-2 ; c = c + 1) begin: gdz
assign summation_steps[c+1] = summation_steps[c] + data[c+2];
end
endgenerate
但是,我们的目标FPGA(XC3S400)没有这么多资源,在这个FPGA上合成这个模块是不可行的。所以,我让这个问题变得更简单了。我假设我们希望输出每N个时钟周期更新一次。有了这个技巧,我们不再需要存储所有收到的数据。我们可以简单地存储求和并将其添加到每个周期的当前输入中。以下代码将起到作用:
always@(posedge clock_in)
begin
if(reset)
begin
signal_out_tmp<=0;
count<=0;
signal_out<=0;
end
else
begin
if(down_sample_clk==N_down_sample)
begin
if(count begin
count<=count+1'b1;
signal_out_tmp<=signal_out_tmp+signal_in;
end
else
begin
count<=0;
signal_out<=signal_out_tmp[27+N2:N2];
signal_out_tmp<=0;
end
end
end
end
在此代码中,总和保存为signal_out_tmp,并将在每个周期添加到输入。在N个点之后,输出将变为signal_out_tmp,并且该变量将被设置为零并开始再次存储总和。
这种方法使用非常低的资源,但其输出将每N个周期更新一次。
模拟
由于它的速度,我们将使用Modelsim进行模拟。我们需要将Modelsim集成到Xilinx ISE。要执行此操作,请转到编辑>首选项>集成工具。在Model Tech Simulator部分,我们输入Modelsim位置,我们就完成了,如图4所示。
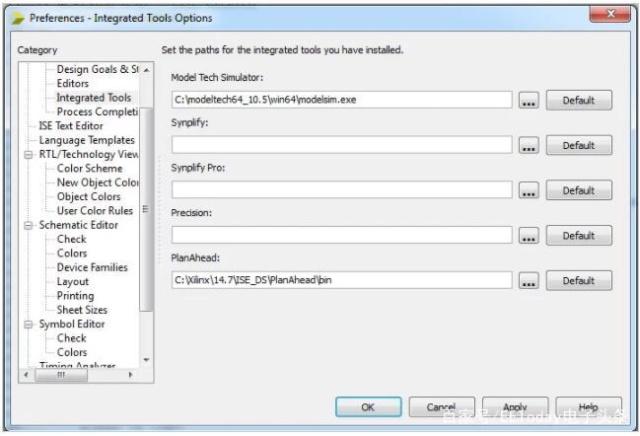
图4.设置模型技术模拟器
Modelsim需要使用XILINX ISE库才能模拟电路。为此,我们需要单击项目上的FPGA模型,然后选择Compile HDL Simulation Libraries,如图5所示。
图5.编译HDL仿真库
测试平台包含在项目代码中,您可以下载。在测试平台中,我们假设输入为步骤并保存输出。在测试平台上读写非常简单,如下面的代码所示。我们可以在测试平台上用fopen函数打开一个文件,然后用fwrite函数写入它。
f = $fopen("output.txt","w");
f2 = $fopen("time.txt","w");
$fwrite(f,"%d %dn",signal_in,signal_out);
$fwrite(f2,"%dn",cur_time);
在fwrite中格式化很像C语言中的简单printf函数。我们还将在测试平台中使用 time变量。使用** time变量为我们提供了可以写入文本文件的当前时间。在模拟我们的项目之后,我们可以使用MATLAB中的书面文件来确保它们是正确的。用MATLAB编写的代码首先读取文件并绘制它们。**
A = importdata('D:low_testoutput.txt');
B = importdata('D:low_testtime.txt');
M2=A(:,2);
M1=A(:,1);
*T=B(:,1)10e-9;
M1=M1/(2^24);
M2=M2/(2^24);
plot(M1);
hold on;
plot(M2);
s=size(M1);
val=0;
t=0:s(1,1)-1;
t=t*50e-9;
for i=405:s(1,1)
- if(abs(M1(i,1)-M2(i,1))<1 .1)* *
val=i;
break;
end
end
stepp=stepinfo(M2,t);
pp=stepp.RiseTime;
fc=.35/pp
cycles=val-405
*time=((cycles)50)/1000
出于测试目的,我们首先使用输入步骤模拟我们的工作台,然后将输入更改为正弦。图显示在图6和图7中。
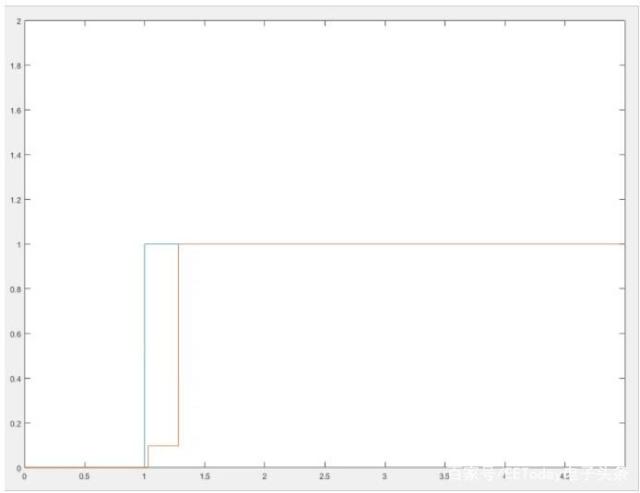
图6.步骤响应
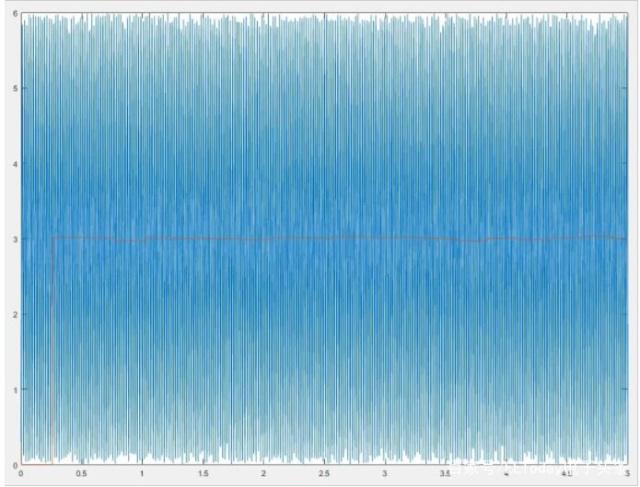
图 7.Sin(x)* sin(x)响应
从图6中可以看出,在0.2ms之后,滤波器输出变得与输入幅度一样高。图6显示了每N个周期的响应,因为输出不会平滑变化。相反,它在第N个周期后发生变化。
在图7中,因为输入是6 * sin(x) sin(x),我们知道这个输入的DC偏移是3,因为我们的低通滤波器输出是3。 *
CIC滤波器
级联积分梳状滤波器是一种硬件高效的FIR数字滤波器。
CIC滤波器由相同数量级的理想积分滤波器和抽取器组成。CIC滤波器架构如图8所示。
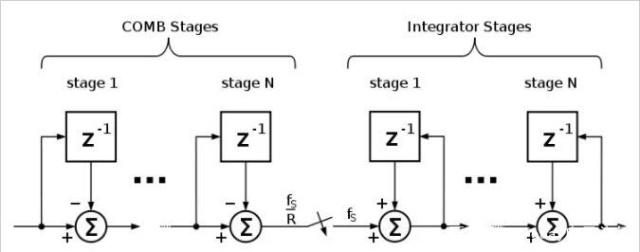
图8. CIC滤波器图像。通过Wikimedia Co
我们可以通过使用CIC滤波器和重写移动平均方程来优化我们的移动平均低通滤波器,如下所示:
**y[n]=∑k=0N1x[nk]=y[n1]+x[n]x[nN].y[n]=∑k=0N1x[nk]=y[n1]+x[n]x[nN].**
该架构由梳状部分(c [n] = x [n] -x [nN])和积分器(y [n] = y [n-1] + c [n])组成,因此我们可以使用CIC架构这里。在这种架构中,我们将加法器减少到只有三个部分,这样我们就可以在每个周期都有输出,这是CIC滤波器的神奇之处。
在可供下载的第二个代码中,使用CIC滤波器拓扑优化移动平均值。我们可以使用以下Verilog代码在硬件中实现上述等式:
wire signed [27+N2:0] signal_out_tmp_2=signal_out_tmp_3+signal_in-data[N-1];
具有sin(x) sin(x)输入的新结构的输出如图9所示。 *
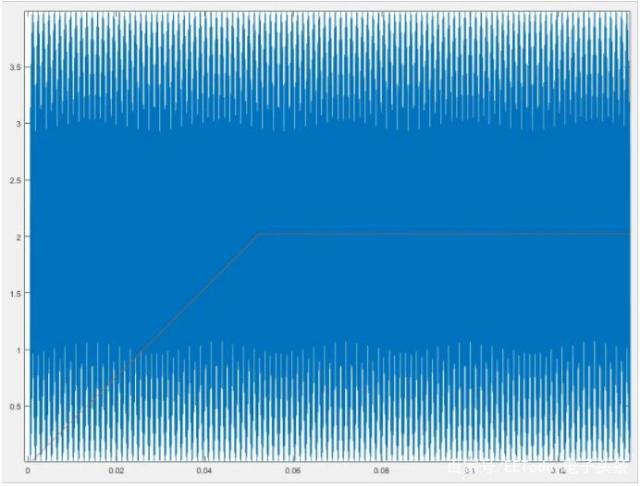
图9. CIC输出
我们的CIC移动平均滤波器的Modelsim仿真在下面的视频中说明。
结论
数字和模拟路由都适用于滤波。每个都有自己的优点,但数字滤波允许重新编程和较小的实现区域。在本文中,我们首先研究了构建滤波器的方法,然后以最简单的方式实现了移动平均滤波器。最后,我们使用CIC架构对其进行了优化。
 电子发烧友App
电子发烧友App












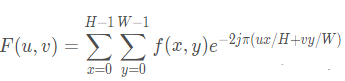










评论