FPGA数字电路时序分析案例

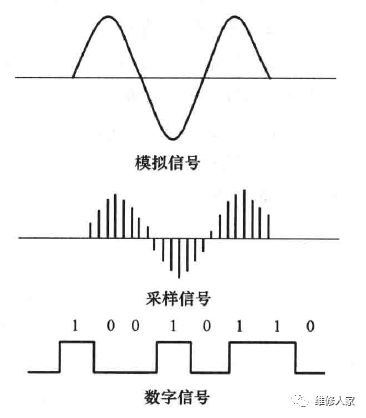
数字电路分为组合( combinational)电路和时序(sequential)电路。组合电路的输出仅取决于它的输入，时序电路的输出取决于当前的输入和之前的输入。组合电路是不需要记忆的，但时序电路有记忆功能。

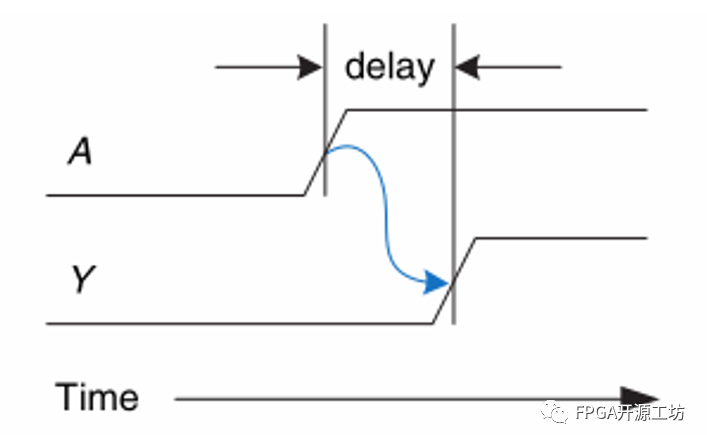
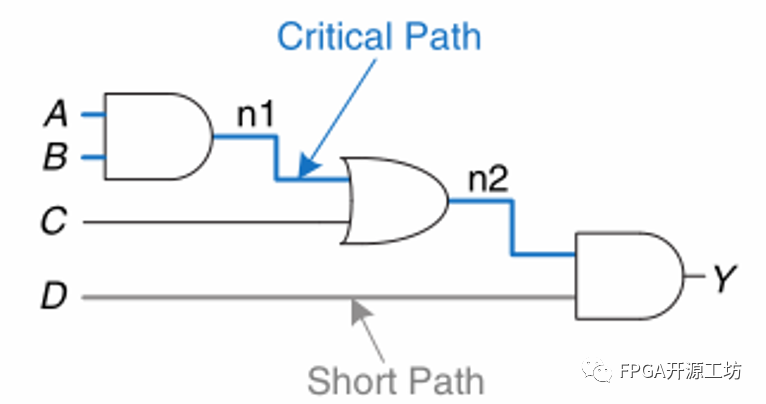
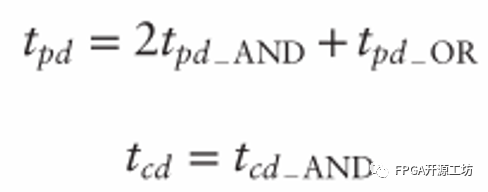
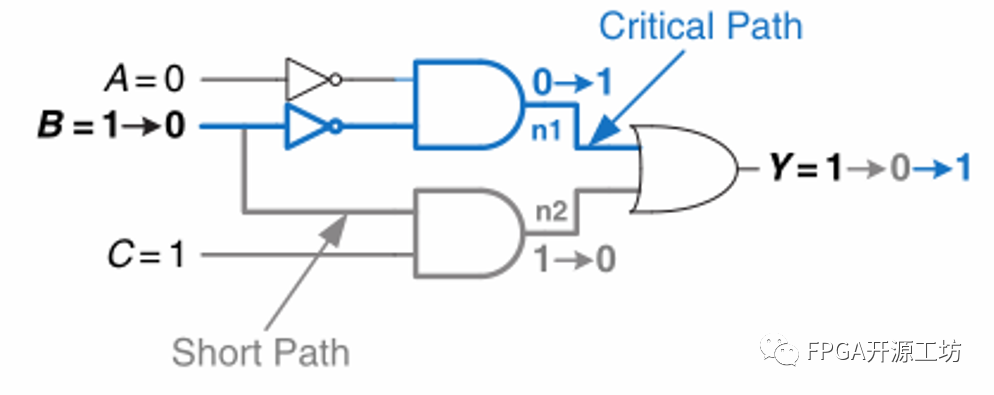
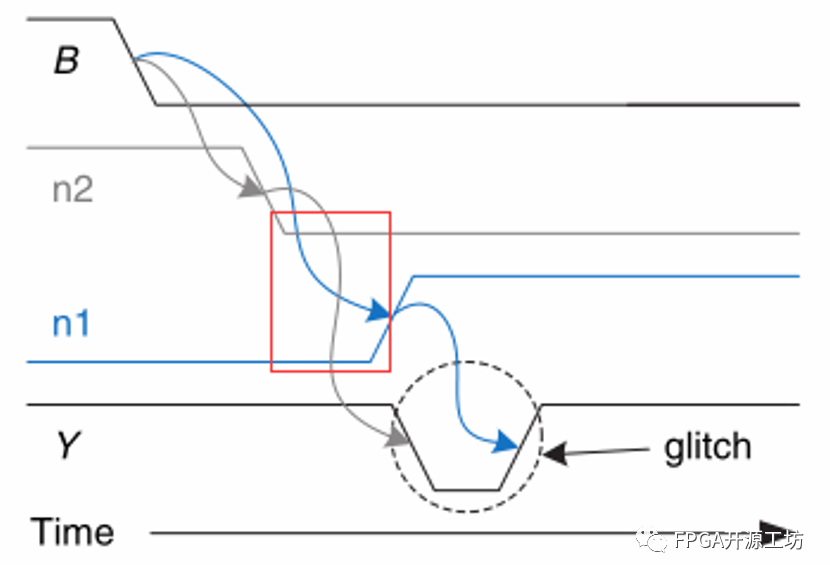
在红色方框处会因为n1n2响应时间的延迟不同导致 OR门产生一个本不期望出现的低电平。尽管很短暂，但在复杂电路中该现象还是会影响某些破坏性的效果。

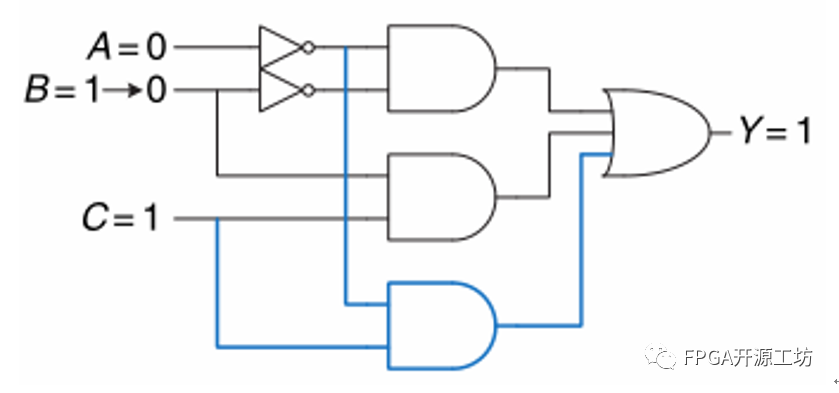
为了防止毛刺出现我们可以修改电路，原因与本节内容无关，所以不展开：

(二)  时序逻辑电路

前面提过，时序逻辑电路的输出响应同时取决于当前的输入与之前的输入状态，所以需要一个存储器件保存之前的出入状态。存储元器件的基本模块为一个双稳态（bistable）的元件。该元件需要有两种稳定的状态，即0和1。我们首先可以想到将两个反相器（非门）交叉耦合（cross coupled），即可形成一个最简单的双稳态电路。

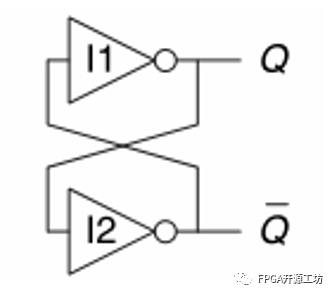
我们可以假设Q为0或1，都可以发现输出始终保持稳定。但是该器件有两个问题：

无法确定Q和~Q的初始值；

没有出入信号。

我们在此基础上需要逐步修改出有实际意义的存储器件。本节关注点在时序分析，所以不做详细分析，只需要抽象化知道功能即可。

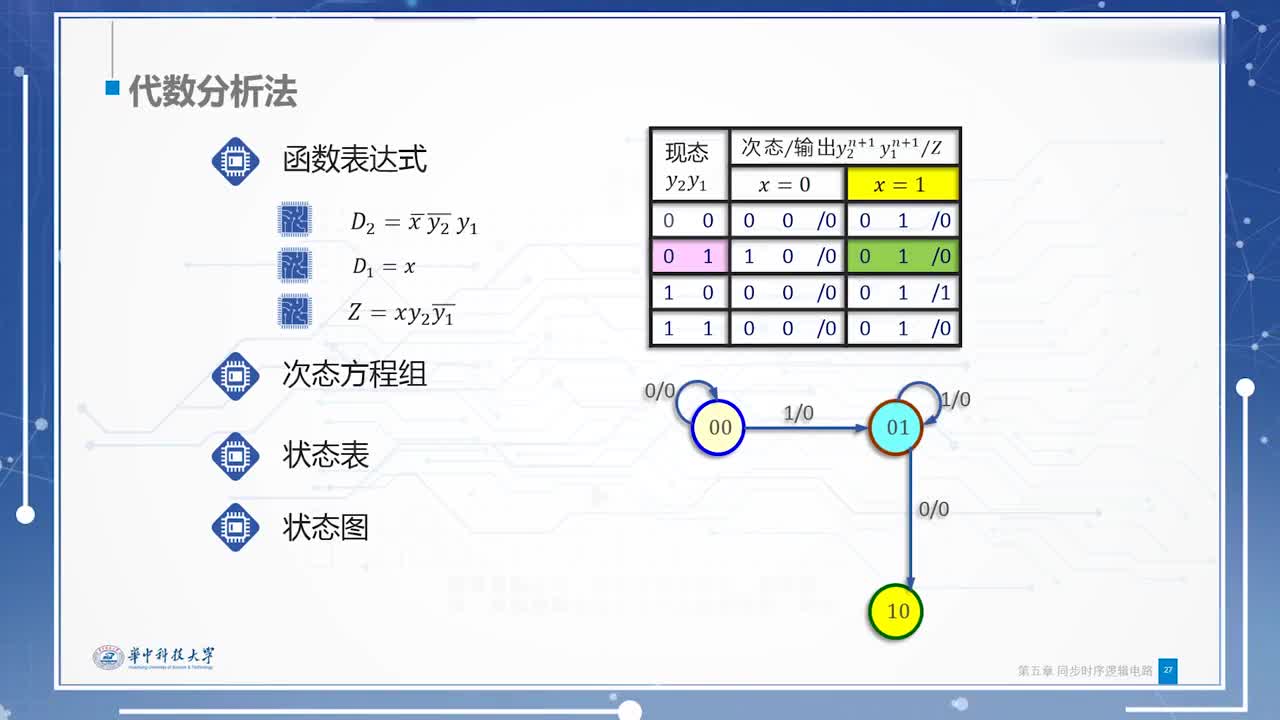
1.    SR锁存器

将非门改为或非门，即SR锁存器。

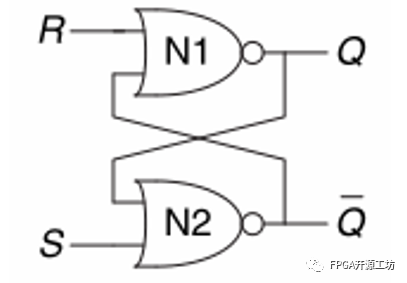
它有置位（SET）和复位（RESET）两个输入信号，以此控制Q的输出。真值表如下：

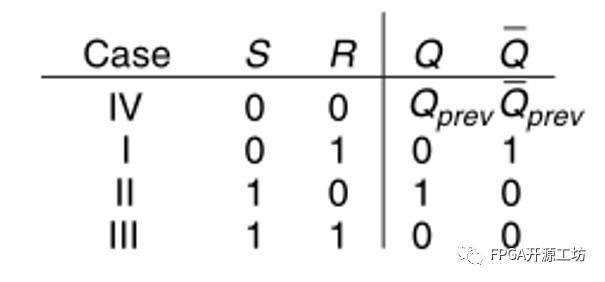
当S和R均为0时，Q可以保存之前的状态。Q也可以通过S和R来控制。但是SR锁存器并没有引入时钟的概念，即它无法决定什么时间来控制Q的状态。

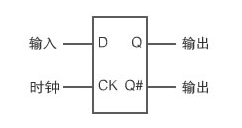
2.    D锁存器

引入CLK，和D信号来决定在何时根据D的状态来控制输出Q电路和真值表如下图：

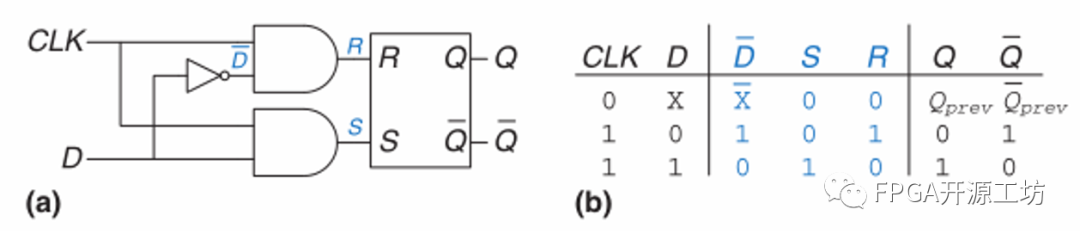
由真值表可知D锁存器（Latch）是电平敏感的，当CLK=1时，Q=D，当CLK=0时，Q保持之前的状态，无视D的变化。

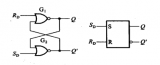
3.    D触发器（filpflop）

我们使用两个由反向时钟控制的D Latch级联（背靠背，back to back）组成DFF，因为反向时钟的作用可以使时钟电平敏感变为边沿敏感，电路如下图：

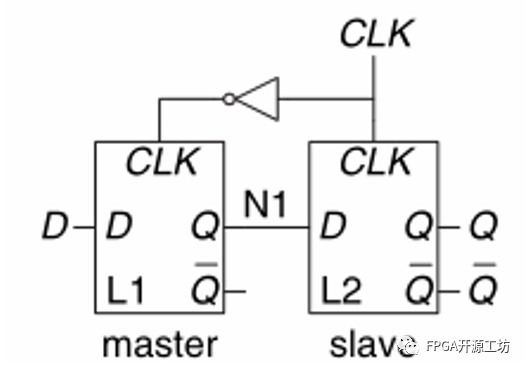
DFF在时钟的上升沿将D赋值给Q，在其它时刻Q保持不变。DFF也常常被称为主从触发器，边沿触发器，正边沿触发器。

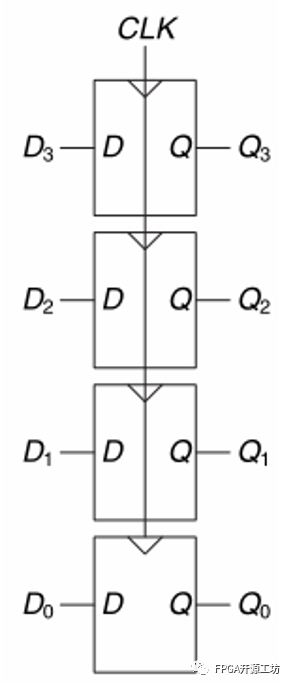
4.    寄存器

将N个共享同一时钟的DFF并联即为N位寄存器，如图：

5.    时序逻辑电路的时序

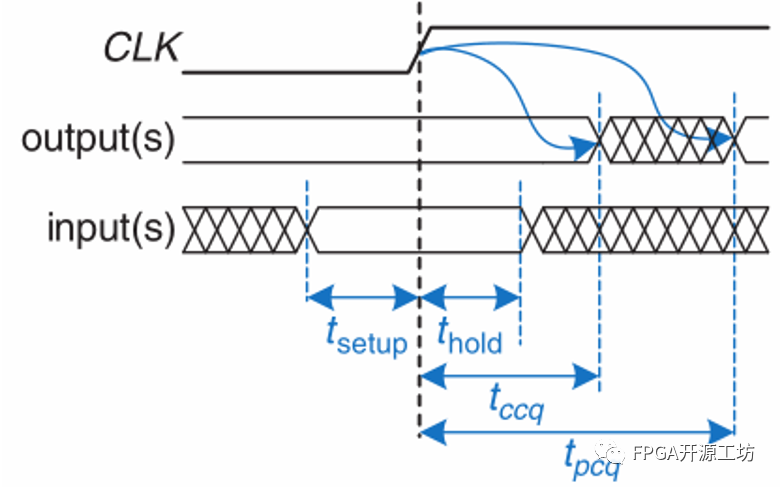
当触发器或寄存器在时钟上升沿到达时将D的值赋给Q，这个过程称之为采样（sampling）。当时钟上升沿时，如果D是0或者1的稳定状态，那么Q也会输出一个稳定的对应值。但如果运气不好，在时钟上升沿，输入D正处于变化状态(比如一个0-1上升的过程中)，那么Q的值将不确定。所以对于Latch和FF我们都有一个约束，即建立时间（setup time）和保持时间（hold time）。

即在时钟上升沿到来之前Tsetup，输入信号必须稳定，且保持到上升沿到来之后Thold时刻。也就是在Tsetup和Thold时刻之间，必须确保输入D保持稳定，才能使Q采样成功。

a)   触发器的动态规范（dynamic discipline）

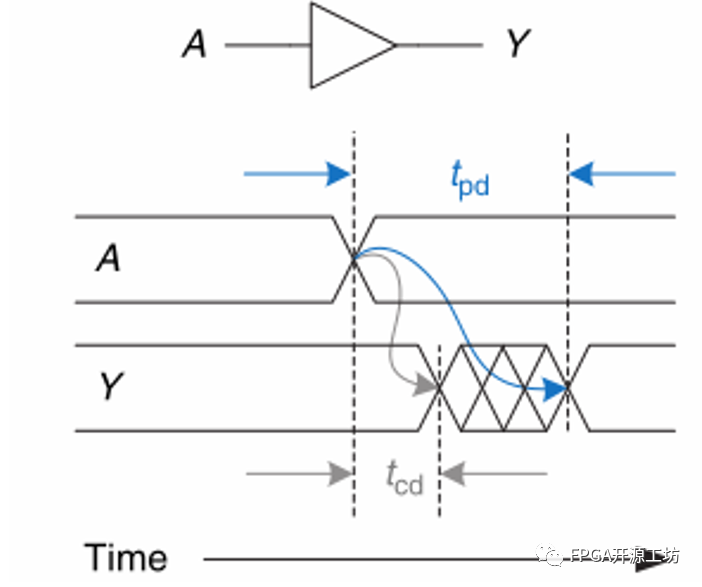
同组合逻辑一样，电子在任何电路元器件传播均需要时间，在latch和FF中也不例外，如下图所示。当时钟上升沿到来，采样输入值后，会经过最短延迟Tccq（Time for ff Contamination Clk-to-Q delay），输出才会发生变化,最迟在Tpcq（flip-flop PropagationClk-to-Q delay）之前稳定下来。

b)   建立时间约束

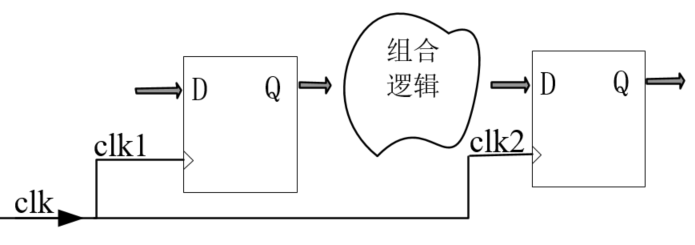
以一个简单的时序逻辑电路（reg to reg）为例，如下图所示：

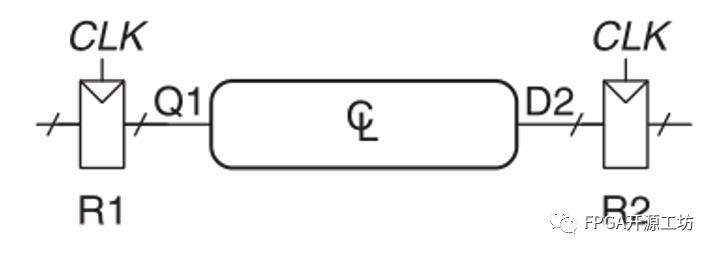
数据从R1输出的Q1开始，经过一个未知的组合逻辑电路并输出D2，进入R2，其中R1和R2的CLK为同一时钟且不考虑布线差异。

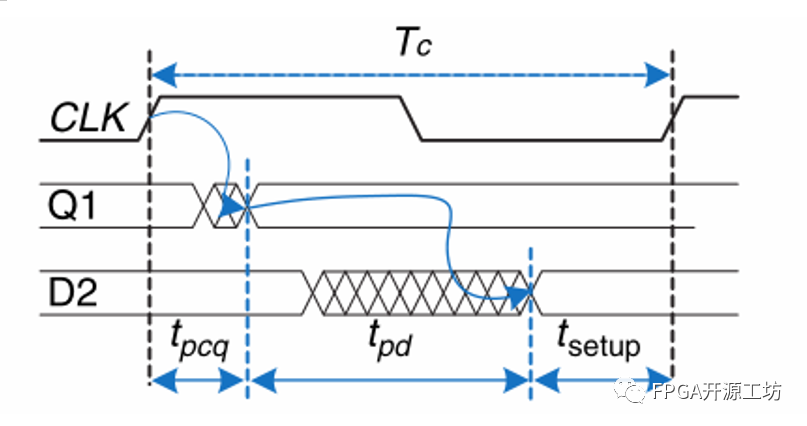
如以上时序图所示，时钟周期为Tc,在一个Cycle内，

我们首先看Q1：

Q1来自寄存器R1的输出，所以Q1必定是不稳定的，看5.a那张时序图，Q1会在第一个CLK的上升沿到来后Tccq和Tpcq之间的某个时间稳定下来，具体时间不知道也不重要，反正我们可以确定最迟Tpcq肯定是稳定的。

随后稳定的Q1会进入组合逻辑电路，最迟经过Tpd时刻稳定下来并输出（不记得Tpd是什么的往前面翻翻，注意要区别于Tpcq），如果这个时刻处在第2个CLK上升沿Tsetup之前，那么第2个CLK就能够顺利采样。

我们就称这种情况为满足建立时间约束。我们可以很容易得到一个等式：

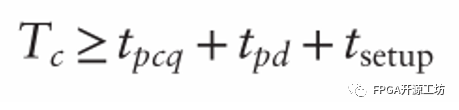
在正常的数字电路系统设计中，系统时钟周期通常由架构师、市场部门决定（以确保产品有足够的性能和竞争力）。或者由设计者本人确定，反正键盘在你手里，你是老大你说了算。Tpcq和Tsetup这是由制造工艺决定的，越先进的制程则延迟越小（或者你是用fpga做产品，那么fpga的型号决定了这两个时钟参数）。所以通常对于设计者来说，为了满足建立时间，你能修改的或者说决定的只有Tpd，即组合逻辑电路的传播延迟。所以我们可以将上述公式变换为：

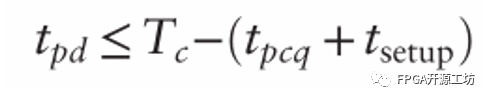
括号内的项Tpcq+Tsetup我们称之为时序开销，反正这是一个由制造工艺或者芯片型号决定的固定值。我们想要Tc更短（时钟频率更快），就要确保组合逻辑的传播延迟不能太大。如果代码是固定的（比如用的ip），组合逻辑的传播延迟没办法缩减，那么就只能降低时钟频率（增大Tc）。

减少组合逻辑的传播延迟主要办法就是减少逻辑的关键路径上的门电路的数量，如果是fpga的话就是减少lut的级联级数。

c)   保持时间约束

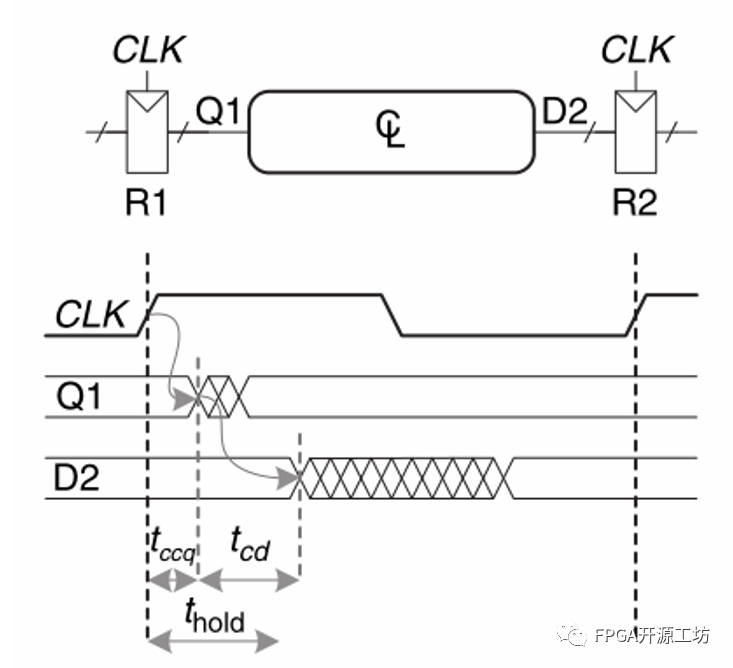
同样关注目的寄存器（destination）R2，R2采样的输入信号是D2，D2来自于经过组合逻辑电路的Q1，Q1来自R1的输出，且在Tccq之前都是稳定的（即使R1的输入变化导致Q1变化，最快也要等到Tccq之后，没想明白的看5.a），在经过组合逻辑电路之后，同理也会在Tcd之前保持稳定，为了确保在Thold之间D2都是稳定的， 会得到下列公式：

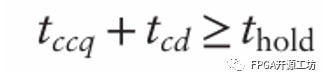
同样Tccq和Thold都是由触发器的制造工艺决定的，所以我们可以变化等式得到：

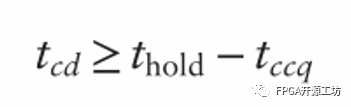
也就是组合逻辑的最小延迟Tcd的值。我们从公式可以发现，满足保持时间约束与系统时钟周期无关，仅与组合逻辑的最小延迟有关。

在实际电路中，我们有一种情况是2个触发器直接级联，中间不经过任何组合逻辑电路：

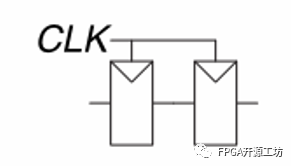
也就是Tcd=0,所以

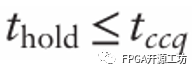
换句话说就是一个可靠触发器的保持时间必定要小于它的最小延迟时间。在实际的数字IC设计中，因为Tcd=0这种情况都能满足，那加了组合逻辑电路Tcd>0必定不会出现不满足的情况。但是因为我们的例子中没有考虑CLK的时钟抖动，以及CLK时钟同源但是布线长度不同而导致的偏移，所以实际也会出现Tcd<0的情况。但是作为前端设计不会关注保持时中违例，而是在用工具生成时序分析报告后由后端通过插入Buffer来处理。在在FPGA设计中，时序分析会在综合和实现两个步骤分别产生，如果综合的时序报告中有保持时间违例一般不做处理(如果违例太大就需要考虑提前进行处理了)，工具会在实现的布局布线阶段自动fix违例。如果布局布线后的时序报告依旧有保持时间违例，一般小于300ps的不做处理，因为工具计算的时候往往是用最差策略来计算的。如果违例数值过于大的话，就要考虑修改代码，或者通过ECO的方式修改时钟BUFF位置，减少时钟偏移。

编辑：黄飞