如何利用LUT来实现FPGA中的DSP功能

作为赛灵思的现场工程师，我常常问这样的问题：我们是否能够提供一款其功能可满足客户所有独特设计要求的DSP内核。有时候内核会太大，太小或者不够快。有时，我们会开发一款能确切满足客户需求的内核，并迅速以CORE GeneratorTM商标推出。不过即便在这种情况下，客户仍然想要一套特定的DSP功能，而且刻不容缓。在这些情况下，我常常建议他们使用我们器件中的插值查找表来定制他们的DSP功能。

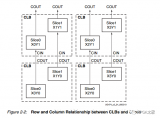
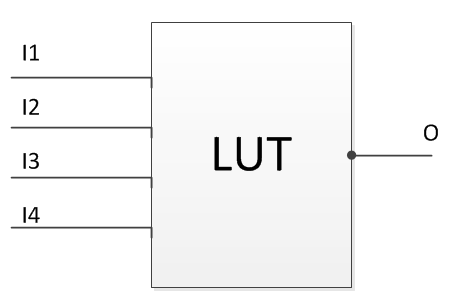
查找表 (LUT) 实质上是一个存储元件，能够根据任何给定的输入状态组合，“查找”输出，以确保每个输入都有确切的输出。采用LUT来实现 DSP功能具有一些重大优势：

您可用诸如MATLAB®或Simulink®等高抽象层编程语言改变LUT内容。
您可以设计一项DSP功能来运行那些采用离散逻辑运算将极度困难的数学函数，比如 y=log(x)、y=exp(x)、y=1/x、y=sin(x) 等。
LUT还可轻松执行在可配置逻辑块 (CLB) 芯片，以及嵌入式乘法单元或DSP48可编程乘法累加 (MAC) 单元方面可能要求过多FPGA资源的复杂数学函数。

不过，以这种方式使用LUT当然也会存在一些弊端。当您使用LUT来实现DSP功能时，您必须使用块RAM (BRAM) 元件。若执行函数 y=sqrt(x)（其中x 表示16位输入，y 表示18位输出），每个变量则需要约64个18KB BRAM单元。如果，比如说，您的目标是实现小型化Spartan®器件，或者您有太多的运算需要执行，无法为每个变量省出64个BRAM单元，建议您放弃这种需要如此大量BRAM单元的方法，从系统架构的角度来看，这种方法代价太大。

插值LUT方法不仅具有LUT方法在实现DSP功能时所带来的各种优势，而且无需使用太多BRAM单元。采用这种方法，您可以使用来自容量较小的LUT （比如，1000字 LUT）的连续输出，线性地对其内插，以模拟更大容量的LUT。这样，您就可以实现比1000 字 LUT 更高的数值分辨率。此外，通过这种方法，仅需 1 个 BRAM、1 个嵌入式乘法器（或DSP48），以及少数几个CLB芯片便可实施控制逻辑，因此LUT的使用成本变得更加合理化。而且，从信噪比的角度来看，其数值精度也是非常让人满意。

当然，应用插值LUT (ILUT) 方法需要一定的技巧。举例来说，采用该方法执行y=sqrt(x) 函数时，可以清楚地显示ILUT在面积占用、时序和数值精度方面的性能。我们先大致看一下这个示例，然后我再讲解部分实例，说明如何使用这种方法来满足客户截然不同的需求，比如让传递函数呈非线性的传感器实现线性化，以及实施自适应有限脉冲响应(FIR) 滤波器以消除合成孔径雷达 (SAR) 图像上的斑点噪声。

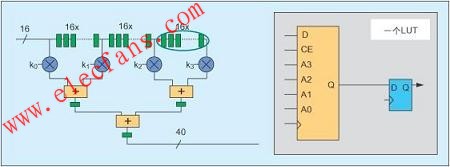
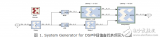
图 1. System Generator for DSP中插值查找表顶层方框图

使用System Generator for DSP进行设计

为在赛灵思FPGA上实施DPS算法，我借助了采用MathWorks Simulink基于模型设计方法的System Generator for DSP设计与综合工具。System Generator得益于赛灵思在Simulink 环境中的DSP模块组，可自动调用CORE Generator为DSP构建块生成高度优化的网表。Simulink是一种双精度浮点设计工具，而System Generator则是一款定点运算工具。不管怎样，您只要将这两种工具协同使用，就可以定义每个信号的总位数以及每个信号的二进制位置，从而在定点运算中巧妙处理分数。仿真结果周期精确、位真，因此您可以方便地将它们与MATLAB脚本或Simulink模块生成的浮点参考值相比较，以检查量化误差。

图1显示了System Generator中ILUT方案的顶层结构图。为让这个方法尽可能一般化，假设nx=16位中的输入变量 x 的取值范围为0≤x＜1，因此其格式为“无符号16位加上二进制点右边的16 位”，也称为Ufix_16_16格式。最高有效位 (MSB) 和最低有效位 (LSB) 模块分别对应输入数据nb=10的最高位和nx-nb=6的最低位。这些信号被命名为x0和dx。y=sqrt(x) 输出则以ny=17位二进制数表示，格式为：Ufix_17_17。

图2显示了1000字小容量LUT通过双端口RAM模块的部署步骤。由于该模块系只读存储器，布尔常数模块We_const强制将写入归零。信号X0和X0+1则用作ROM表上后续的两个地址。Data_const模块的零常数定义了任何ROM字的大小（即本例中的ny）。

下面的公式显示了以x0为x的最高有效位的情况下，如何在两个已知点（x0，y0）和（x1，y1）之间插入坐标为（x，y）的点：

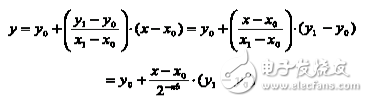
注意X1和X0是这个小容量LUT的相邻地址，它们之间只隔了一个最低有效位。由于这个小容量LUT的地址空间为nb 位，那么该LSB的值为2-nb。

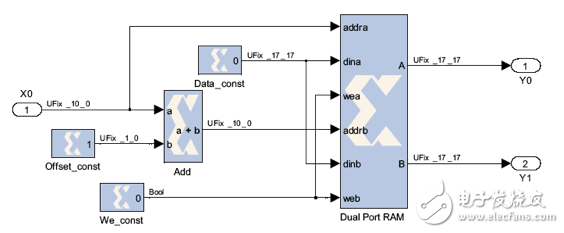
图2 System Generator for DSP中的小容量LUT图

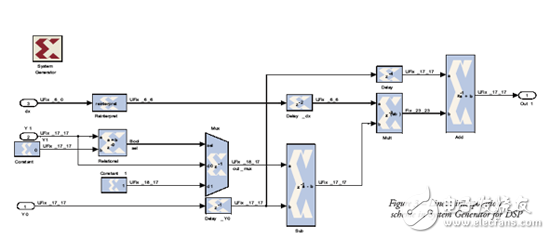
图3 System Generator for DSP的线性内插图

内插步骤见图3。“Reinterpret”模块在不改变二进制表示法的情况下，可改变dx=x-x0信号。其重置了二进制小数点（从UFix_6_0到UFix_6_6格式），并输出nx-nb位二进制数的一个分数，从而计算出 (x-x0)/2-nb 的值。

从硬件角度来看，这些模块什么都不占用。总的来说（且根据我们通过ILUT方法应用的函数类型），如果y1=0且y0=0，我们可以强制y1-y0=1，这样我们就可以得到1/2-nb而不是0。我们采用Mux、Rational、Constant和Constant1模块来执行这项工作。剩下的Mult、Add和Sub模块则执行线性内插公式。在本例中，我强制Mult模块的输出信号为17位分辨率，而非理论上要求的23位，因为总体数值精度对本试验来说已经足够。此外，由于y-sqrt(x) 函数呈单调递增，因此所有结果都无符号。换句话说，不同的函数需要对数据类型进行不同的精心调整，但不会与图3所示的原理相去甚远。

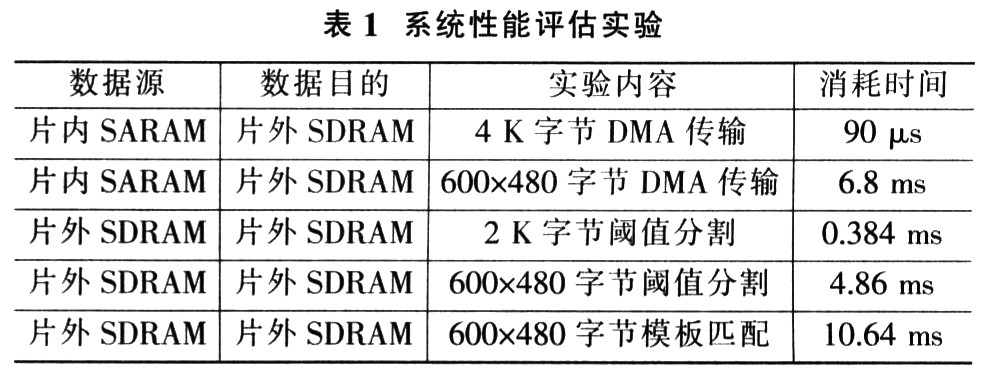
假定我们以Spartan-3E 1200（fg320-4）为目标器件，现使用ISE设计套件和System Generator for DSP 10.1 SP3版工具对其进行布局和布线，结果其所占用的FPGA资源的总体情况如下：

该设计完全流水线作业，可以在任何一个时钟周期提供新的输出。时延为10个时钟周期，最大数据速率达194.70MSPS（每秒百万采样数）。从数值精度来说，对1000或2000字ILUT而言，参考浮点结果与System Generator for DSP定点输出的量化误差之间的比值，即信噪比分别为 71.94dB或77.95dB。

除ILUT外，我们还可应用赛灵思System Generator for DSP提供的Reference Math Blockset（参考数学模块组）中的CORDIC SQRT模块。在本例中，总时延为37个时钟周期，最大数据速率达115.18 MSPS，区域资源占用为940片触发器，总共有885个四输入LUT，560个占用的芯片以及两个MULT 18x18嵌入式乘法器。信噪比为40.64dB。这些结果显示CORDIC是实施定点数学运算的理想方法，但ILUT在许多方面更加出色。

线性化非线性传感器

目前许多企业在工业控制系统中使用“智能传感器”，以满足低占用面积、低功耗、高性能、最低成本以及最短开发时间等要求。通用智能传感器可视为一个由传感器及其信号控制线路、模数转换器 (ADC) 、带或不带嵌入式处理器的相关DSP子系统组成的功能组件，所有这些功能块都集成在的同一器件上，如图4所示。

智能传感器的目的是将物理量（如电机中的电流）转化为数字电路能够处理的数字信号。构建这类传感器所采用的技术及组件的某些特性通常会导致诸如失调、增益和非线性等误差，进而导致总体传递函数呈非线性。

一般来说，客户会校正他们产品中运行的DSP子系统所出现的上述误差。如果 y=f(x) 是来自传感器和ADC级联的数字输出信号，那么DSP必须执行其反函数g(y)=f-1(y) 来补偿非线性函数，这样总体输出z即为：

这是直线方程，其斜率为m，纵截距为b。

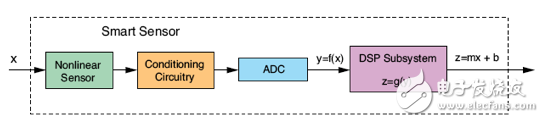
图4. 智能传感器的方框图

最简单的线性化方法是LUT法，采用存储在ROM中的传感器校准点。不过，对16位的ADC来说，ROM显得过大了，且需要64个BRAM单元。而内插LUT则不然，是一个良好的解决方案。

举例来说，我们假定非线性传递函数是一条抛物线。下一 MATLAB分段码说明了如何生成最终直线的m和b参数，以及如何计算 g(y)（即 f(x) 的反函数）。图5用三种颜色显示了三条不同曲线。请注意在计算 f(x) 的反函数 g(y) 过程中会丢失一些值。这是因为有几个y值相同的点对应着不同的x点。因此，需要对 g(y) 进行平滑化，填补所有缺失的点。（为精确起见，我没有把这部分运算包括在MATLAB分段码中）

图5.黑色抛物线表示非线性传感器传递函数f(x) 的曲线；绿色直线表示线性化DSP子系统获得的最终线性传感器传递函数曲线；蓝色抛物线则表示反函数g(y) 的曲线。

我采用非常类似于图1-3的设计，在System Generator for DSP中运行基于定点周期的仿真，在非线性传感器的总体输出范围内得到了92.48dB的信噪比。

斑点噪声消除

跟踪高速运动系统的目标物体（比如导弹）是一项极富挑战性的工作，需要非常复杂的DSP算法以及诸如合成孔径雷达 (SAR) 等各种不同类型的探测介质。作为典型的相干电磁源（如激光），SAR成像器件也受斑点噪声的影响。因此，任何基于SAR的DSP链的第一级都是二维 (2D) 自适应FIR滤波器，用以降低这种噪声（但不可能完全消除）。图6显示了斑点噪声的MATLAB仿真。该噪音对左边图像的画质造成了综合性的不良影响。右边的图像是2D FIR滤波器黄金模型的输出结果。

图 6. 斑点噪声对左边图像画质造成了影响，右边的是滤波后的图像

斑点噪声是一种倍增噪声，呈指数分布，完全由其方差值σ决定。因此，广泛使用的抗斑点噪声的方法就是Frost滤波器（由发明者 V.S.Frost的名字命名而来）。V.S.Frost 在1981年发表的论文对这个现象进行了探讨。在一个3x3的矩阵中，可以用下列公式进行建模：

其中xij和yij分别代表Frost滤波器的输入和输出采样。K 是控制滤波强度的增益系数（为方便起见，我在下面假定K=1），μ1和σ分别是2D内核的平均值和方差值，Tij是中心输出像素（系数ij=22）及所有周边像素的距离矩阵。下面的等式说明实施这个滤波器的关键因素是R1，即3x3矩阵中的一阶μ1和二阶μ2之间的比值：

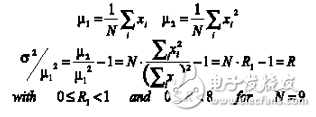
R1的取值范围在0和1之间。根据实验发现要取得良好的数值精度，R1可以使用16位至20位二进制数来表示。

我在system Generator for DSP中设计R1计算步骤后，我决定通过内插LUT来实施滤波系数的归一化。LUT的内容以下列MATLAB代码表示：

图7显示的是归一化后的系数沿R1输入信号分布的曲线。这里只有三条曲线，因为 Tij矩阵在系数 ij=22的中心像素周围呈对称分布。根据曲线，与纯浮点参考模型相比，数值结果显示信噪比介于81.28至83.38dB之间。对有兴趣的读者，下面的MATLAB分段码说明了2D滤波器的处理过程（为简便起见，没有包括ILUT函数）。

图7 沿斑点噪声降噪滤波参数 R1 分布的归一化系数

简言之，这些例子说明插值查找表是实施赛灵思FPGA的DSP功能的简便而强大的方法。插值查找表可帮助您在保持面积占用相对较低的情况下实现极高数值精度 (SNR) 和高数据速率。