引言
数字滤波器在语音与图像处理、模式识别、雷达信号处理、频谱分析等应用中都具有重要作用。它能避免模拟滤波器所无法克服的温漂和噪声等问题, 同时比模拟滤波器精度高、稳定性好、体积小、更加灵活, 因而得到广泛应用。在声波测井中, 通常需要对信号进行精确的滤波,并且对滤波器具有严格的实时性要求。本文利用辅助Matlab设计工具, 设计了一种基于FPGA且可满足测井需求的高阶快速数字滤波器。
1 线性相位FIR滤波器结构
数字滤波器的种类很多, 分类的方法也不尽相同。从数字滤波器的单位冲击响应来看, 数字滤波器分为有限冲激响应数字滤波器(FIR) 和无限冲激响应数字滤波器(IIR)。相对于IIR滤波器,FIR滤波器可以进行准确的线性相位设计, 而且其结构具有稳定的量化滤波器系数。针对于声波测井处理具有线性相位要求的声波信号, FIR滤波器是首选。
在时域中, FIR滤波器的输入输出过程是一个输入信号与单位脉冲响应进行线性卷积的过程, 其差分方程表达式为:
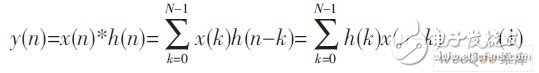
其中, y (n) 为滤波输出, x (n) 为采样数据, h (n) 为滤波器抽头系数。其结构如图1 (a)所示, 图中, N-1阶FIR滤波器要用N个系数描述, 通常, 需要N个乘法器和N-1个两输入加法器才能实现。不难发现, 乘法器的系数正好是传输函数的系数, 因此, 该结构且称为直接型结构。
对于系数对称的FIR线性相位滤波器, 可将式(1) 写成如下形式:
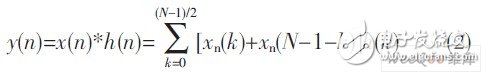
系数对称的改进型FIR滤波器的结构如图1(b) 所示。该结构把系数对称(相同或相反) 的抽头合并之后再作乘法, 这样可使乘法器数量降为原有的一半, 但也增加了额外的加法器。
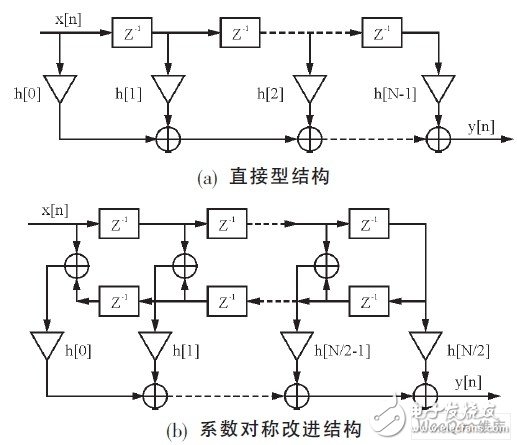
图1 FIR滤波器结构
2 设计方法与指标
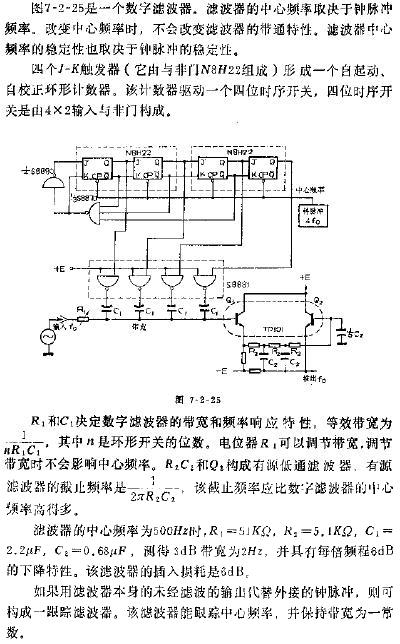
FDATool是Matlab信号处理工具箱里专用的滤波器设计分析工具, 该工具的主要作用是按照设计指标提取滤波器系数。用FDATool设计数字滤波器的关键在于滤波器类型、窗函数、滤波器阶数、截止频率等参数的选择。其中窗函数用于决定阻带衰减和过渡带带宽, 常用的窗函数有矩形窗、汉宁窗、海明窗和布莱克曼窗。矩形窗和汉宁窗阻带衰减较小, 而布莱克曼窗过渡带较大, 相对来说, 海明窗更符合设计要求, 它的最小阻带可以达到54.5dB, 归一化过渡带带宽为3.11π/M (滤波器阶数N=2M+1)。针对声波测井信号, 设计时应进行表1所列的参数设置。
表1 滤波器参数选择
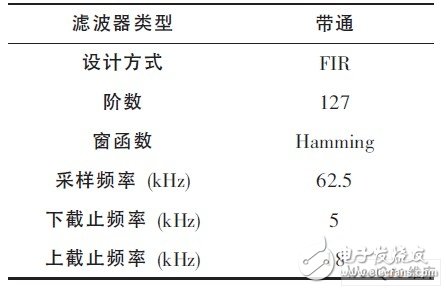
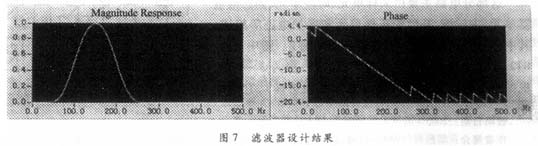
图2所示是该滤波器的幅频和相频响应曲线,该曲线在通带内保持线性相位, 阻带衰减大于52dB, 过渡带带宽为1.65kHz。抽头系数可以在工具箱中量化为定点整型数据, 以便在FPGA实现阶数为127的滤波器, 该滤波器一共有128个系数。对于阶数较大的滤波器来说, 其量化对阻带衰减和过渡带的影响极小。
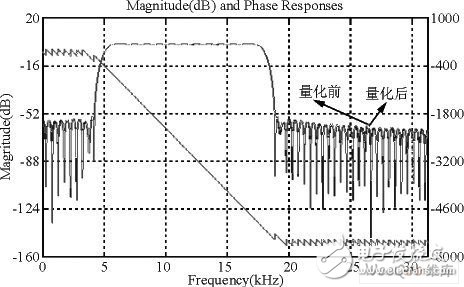
图2 滤波器幅频和相频响应特性曲线
3 基于FPGA的滤波器设计
用FPGA设计FIR滤波器的关键在于如何处理占用大量资源的乘法单元。分布式算法(DA) 的提出可将乘法运算转换为移位相加运算, 从而节约硬件资源。若令Hk为滤波器系数, xk (n) 为n时刻的采样输入, y (n) 为n时刻的系统响应, 那么, 式(1) 就可以等效于下式:

把数据的源数据格式规定为2的补码形式,则有:
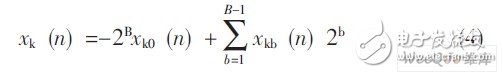
式中, xkb (n) 为二进制数, 可取值为0或1;xk0 (n) 为符号位, 为1表示数据为负, 为0表示数据为正。因此, 将(4) 式代入(3) 式可得:
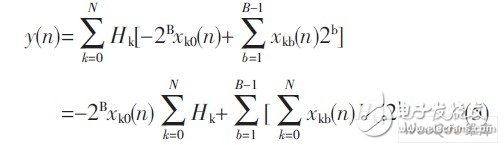
式(5) 的形式被称为分布式算法。可以看出, 方括号内表示输入变量的一个数据位和所有滤波器抽头系数H0~HN的每一位进行“与” 运算并求和。而指数部分则说明了求和结果的位权,整数乘以2b就是左移b位, 对此可以通过硬件连线来实现, 而不占用逻辑资源。这样就可以通过建立查找表来实现方括号中的运算。查找表可用所有输入变量的同一位进行寻址, 这便是基于查找表的分布式算法(LUT-DA)。
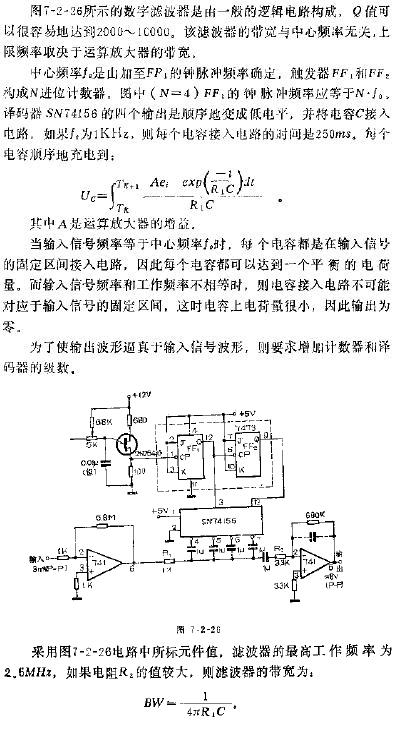
LUT-DA算法的查找表大小为B·2N bits, 其中B为输入数据的位宽, N为滤波器阶数。随着滤波器阶数的增加, 查找表大小是2的指数增长;当B为16, N为128时, 查找表的大小已经不可想象。故将查找表分割成多个子表, 可以有效解决这个问题, 这也衍生了比较有效的串行LUT-DA算法和并行LUT-DA算法, 但两者都有不足的地方。对于串行结构, 要完成一次输出, 需要大于B的多个时钟周期; 而对于并行结构, 虽然可以一个时钟周期完成一次输出, 但需要复制B个完全相同的LUT表, 而这会增加硬件资源的开销。
为了兼顾速度和面积, 本文设计了一种基于DA算法原理的CSD-DA算法。首先, 将系数式(3) 中的固定系数Hk按2的幂展开后可得:
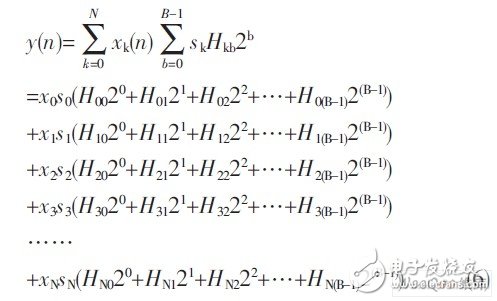
然后交换移位和累加顺序, 则可得到下式:
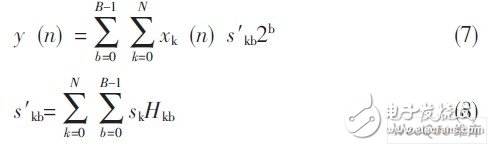
式中, Hkb是值为0或者1的权重系数; Sk为1表示Hk为正, 为-1则表示Hk为负; s′kb的值可取0、-1或者1。经过(4) 式的展开, 乘法运算将被全部转换为移位相加运算, 其中权重为0的部分可以剔除而不进行计算。为了更进一步减少Hkb阵列中的非零项, 可将Hk编码为CSD码, 即从二进制编码最低的有效位开始, 用10···01来取代所有大于或等于2的1序列, 1表示该位为-1。由于CSD表示其中任何相邻的两位中, 必包含一个0,故1的数量最多不会超过N/2。平均来说, CSD表示其中大约有1/3的位为非零值, 这比补码表示少大约1/3的非零位。假设h= (15) 10= (01111) 2,y=hx=x (23+22+21+20), 而如果将(15) 10编码为(10001) csd, 那么, Y=x· (24-20)。采用二进制编码方式, 将用到3个加法器, 而用CSD编码, 则只用了一个减法器, 可见, CSD编码可以从本质上减少硬件资源开销。经过CSD编码优化后, s′kb非零值的个数会远小于Hkb的非零值个数。
对于线性相位系数对称的FIR滤波器, 为了减少乘法单元, 可选择图3所示的结构。由于所有的乘法运算都可转化为大量的加法和减法运算, 故将导致关键路径过长, 系统运行速度较低。而加入流水线寄存器, 则可减少关键路径长度, 从而提高系统的最大工作频率。在b为定值时, s′kb的非零值个数存在不确定性, 故在进行流水线设计的时候, 可根据s′kb进行灵活的分割, 路径越长, 加入的流水线寄存器越多。为了防止中间结果的溢出, 寄存器的位宽要有冗余设计, 对于有符号的数, 其位宽取值为M+log2N-1, M为上级累加器位宽, N为滤波器阶数。
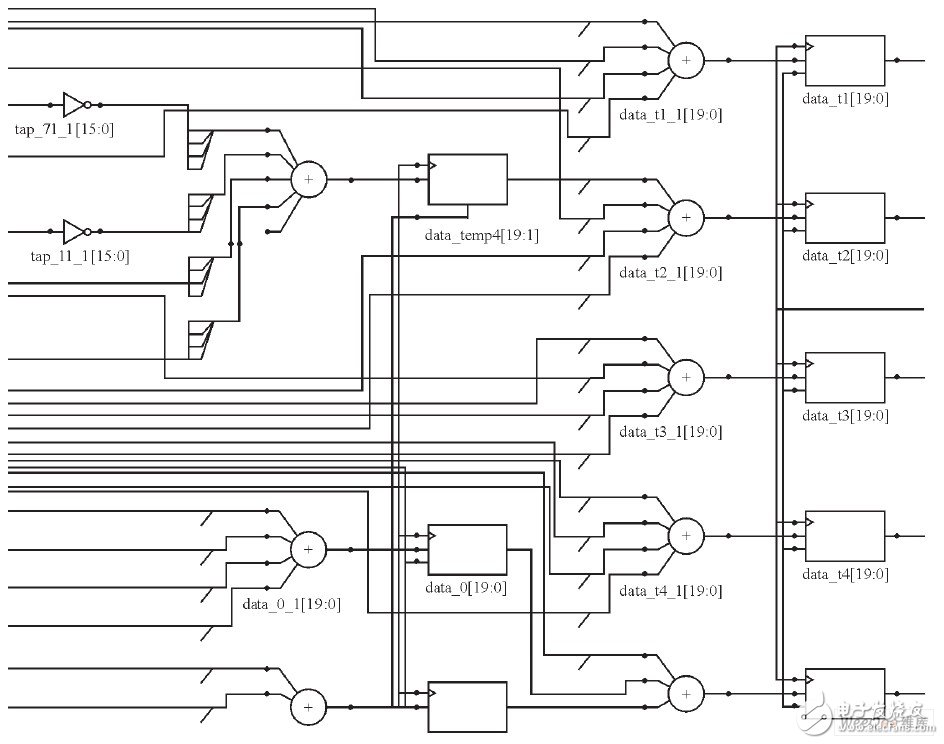
图3 流水线CSD-DA算法局部结构
从图3的流水优化CSD-DA算法结构可见, 所有乘法都会转换为移位加法, 移位运算可用硬件连线实现, 整个结构经过了合理的流水线分割。
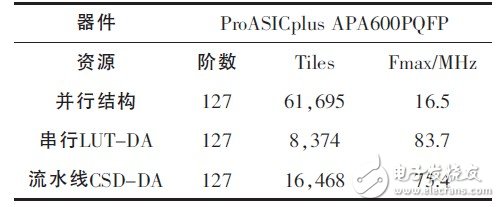
表2所列是不同结构滤波器的综合结果。其中并行结构是最差的一种结构, 它占用资源多、速度慢; 串行LUT-DA结构, 虽然占用资源少,最大工作频率高, 但毕竟是串行结构, 不能在一个时钟节拍完成对一个采样点的滤波运算; 而流水线CSD-DA结构则无论在速度, 还是面积上,都具有比较明显的优势。如果工作时钟为75MHz, 那么, 一个时钟节拍便可以完成一次输出, 处理330个采样点的单通道信号仅需4.4μs,可以满足测井实时性要求。
表2 滤波器的综合结果
4 结果分析
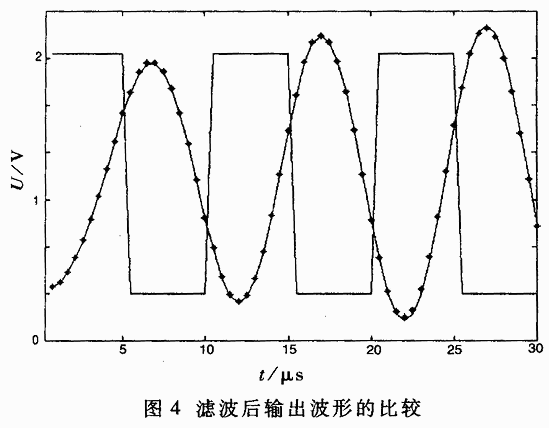
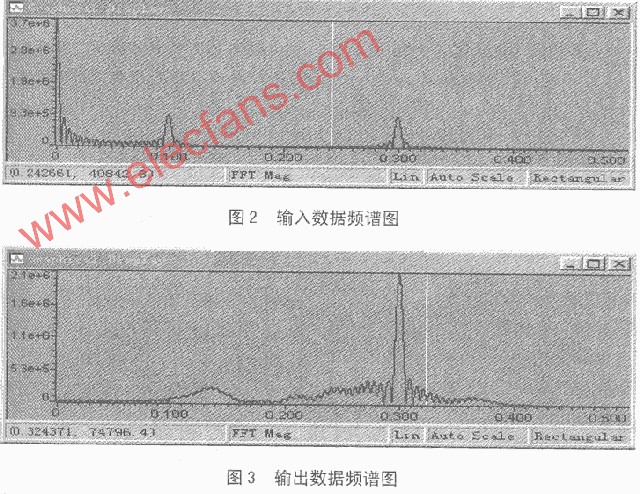
为了验证滤波器的功能是否正确, 可对本设计在Modelsim中进行仿真。若原始波形为带噪声的声波信号, 那么, 其滤波的结果如图4所示。
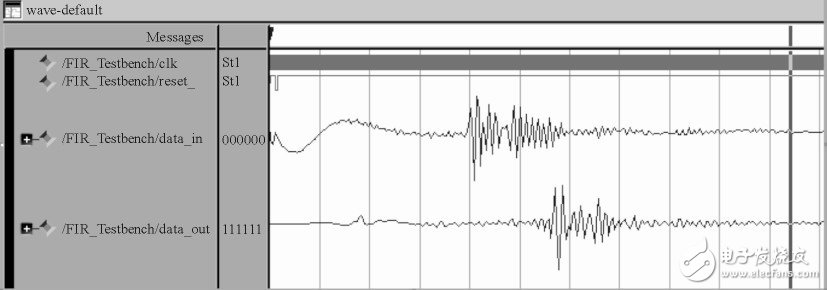
图4 滤波器在Modelsim中的仿真结果
图5所示是滤波器在Matlab中的仿真结果, 可以看出, Modelsim和Matlab的仿真结果一致。在频域上, 对比图5 (a) 和图5 (b) 可以看到, 其滤波后的波形只保留了5kHz~18kHz的频谱部分, 这说明流水线CSD-DA结构的数字滤波器设计正确。
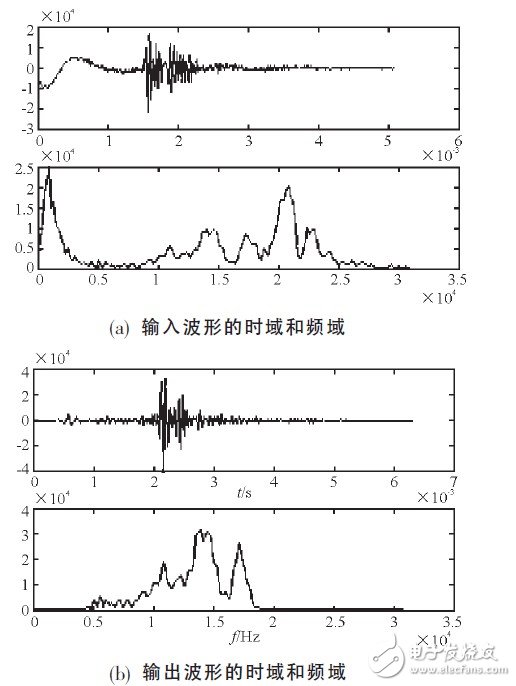
图5 滤波器在Matlab中的仿真结果
5 结束语
本文详细讲述了通过Matlab工具设计FIR线性相位滤波器的方法, 并针对声波信号设计了优于传统结构的流水线CSD-DA结构, 该结构具有较明显的速度和面积优势。文中也通过仿真实验证实了设计的合理性和正确性。但值得指出的是, 该结构只适合固定滤波器系数的场合, 而如果要进行修改, 则需要重新对系数进行CSD编码和流水线分割。
 电子发烧友App
电子发烧友App












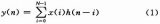
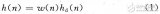












评论