人工神经网络在智能控制、模式识别、图像处理等领域中应用广泛。在进行神经网络的应用研究时,人们可以将神经网络模型或算法在通用的计算机上软件编程实现,但很多时间浪费在分析指令、读出写入数据等,其实现效率并不高。软件实现的缺点是并行程度较低,因此利用软件实现神经网络的方法无法满足某些对数据实时处理要求较高的场合(如工业控制等领域)。
目前实现大规模、实时性要求高的神经网络,传统的软件算法实现方法显示出其难以满足速度等要求的不足。此外,在构建神经网络时必然需要考虑硬件实现问题。由于神经网络具有并行计算的特点和功能,可以有效发掘算法本身的并行特性,提出高效的硬件电路结构,从而完成神经网络的硬件实现。
脉冲耦合神经网络(Pulse Coupled Neural Network,PCNN)是新一代的神经网络,在研究猫等哺乳动物的视觉神经元时,根据其脉冲同步发放的工作原理所提出的。目前,P CNN理论仍在发展中,由于其独特的并行性能,在图像分割与平滑、边缘检测与细化、决策与优化等领域应用广泛。当前的研究重点在于模型的优化和软件的实现,而相关的硬件实现在国内并不多见,PCNN并行结构的特性为硬件实现提供了可能。
1 PCNN的基本原理
脉冲耦合神经网络是一种单层模式的两维神经网络,它的基本单元是脉冲耦合网络的神经元。图1为PCNN的单个神经元模型框图,它由输入部分、连接调制部分、脉冲发生器部分3部分构成。
输入部分即接收域,其接收信号来源有两部分:邻近神经元产生的信号和外部的输入激励。这两部分信号通过两个不同的路径进行传递,其中一个路径传递反馈输入信号,其包含外部输入激励,该路径即为F路径;另一个路径传递连接输入信号,其包含来自邻近神经元产生的信号,该路径即为L路径。
连接调制部分完成上述两个路径信号的耦合,经过一定的信号处理,产生神经元的内部活动项。该信号处理需要首先通过一个正的单位偏置和L路径的连接输入信号的累加,然后与F路径的反馈输入信号完成相乘调制。该神经元的内部活动项即为信号经调制得到的乘积结果。
脉冲发生器和阈值大小变化的比较器构成PCNN单个神经元的脉冲发生部分。如果达到脉冲发放条件,则该脉冲发生器起作用,发出一个频率恒定不变的脉冲,此时神经元处于点火状态。
根据图1模型,每个神经元按照公式(1)完成迭代运算,实现上述PCNN的功能。
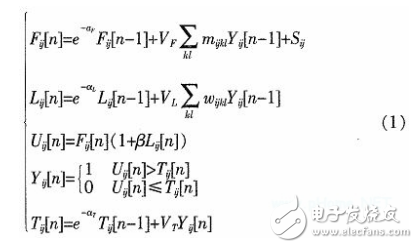
式(1)中,Fij[n]是某个神经元的第n次反馈输入信号;αF与αL表示迭代时间常数;Sij表示外部输入常数,在图像处理时即为像素矩阵中像素的灰度值;Lij[n]是神经元的线性输入项;wijkl与mijkl表示突触间联接权值系数;Uij[n]是神经元的内部活动项;Tij[n]是Uij[n]是否激发生成脉冲的动态阈值;β是神经元突触间的连接强度系数;Yij[n]为PCNN的脉冲输出项。由于信号Lij[n]比信号Fij[n]变化快,经过相乘调制的信号Uij[n]就等同于把一个快速变化的信号加在一个近似不变的信号上。
如果某个神经元点火,即发出一个脉冲信号,那么由于内部活动项大于当前的门限阈值,下一次迭代运算后阈值将通过其时间常数αT和幅度系数VT突然变大。而此时迭代后的阈值Tij[n]远大于Uij[n],因此神经元将被抑制,脉冲信号停止输出,即处于未点火状态。在这一状态下,周围神经元不断点火,产生响应的脉冲信号,通过L路径的输入提高内部活动项,与此同时阈值经指数运算不断较小。在某一次迭代时,当前阈值将再次小于Uij[n],此时神经元将被激活,脉冲信号开始输出,即神经元再次被点火。如此周而复始,不用神经元在点火和为点火状态进行切换,从而实现脉冲同步激发。
2 系统硬件实现
2.1 PCNN模型的改进
对于上述PCNN模型结构,在图像处理等应用中仍存在一定的局限性:
1)PCNN涉及到的参数较多,增加了数学运算的难度,实现算法比较困难;
2)网络参数确定较为困难。
此外,为了易于FPGA实现。把标准的PCNN进行一定的简化和改进。将反馈输入只当做对应象素的灰度值强度,所以F路径的连接权值矩阵M为零。改进后的第一个优点是减少了迭代的时间,而迭代的质量仍与标准PCNN模型接近,第二个优点是节约了FPGA资源的利用。改进模型的数学表达式与标准模型相似,只是馈送域不同。馈送域表达式为:
Fij[n]=Sij (2)
2.2 小数的定点表示方法
由于Vetilog无法直接定义小数类型,所以采用小数的定点表示法表示小数。考虑到灰度值为8位二进制数据,故小数的表示形式为《8.8》,即整数位数和小数位数都为8位,整数的表示形式为《8.0》,即整数位数为8位,小数位数为0位。由于并没有存储小数的位置信息,所以需要根据先前的约定对最后的结果进行截取。如式(3)所示,最后的运算结果为24位,低8位为小数部分,而利用Verilog的位操作运算截取中间8位即为更新后的灰度值。
《8.8》*《8.0》+《8.8》*《8.0》=《16.8》 (3)
2.3 PCNN参数选择
利用2.1节介绍的PCNN改进模型,描述单个神经元的PCNN算法。表1为本设计方案PCNN模型参数的经验设定,其阈值衰减设为每次运算后阈值的约0.9倍。为使算法利于硬件实现,实验中将设定神经元连接强度β=1,连接域增益VL=1。
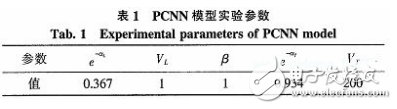
其连接域邻域矩阵为:

2.4 系统整体设计框图
在进行图像处理时,需要把神经元与像素一一对应,神经网络的大小取决于图像的大小。如果需要处理的图像体积较大,那么硬件资源将被大量占用,继而需要更高规格的FPGA芯片来实现。本文介绍一个简单的PCNN硬件系统,可以处理3×3、8位的灰度图像。
PCNN在FPGA实现的系统框图如图2所示。系统分为5个主要的功能模块:时钟分频模块、串口接收模块、串并转换模块、PCNN模块和VGA显示模块。图中除PC机部分都在FPGA上实现。PC机包含上位机串口通信软件,常见的有VB串口通信助手、串口大师等,可实现串口的调试、测试、监控和过滤等功能。
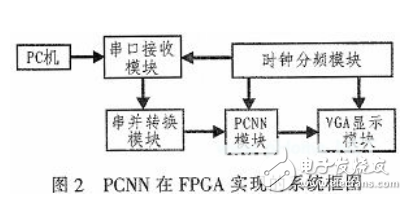
系统需要完成的工作分为三大部分:图像的输入、图像的处理和图像的显示输出。系统详细的工作过程描述如下:PC机通过串口软件(如串口大师)发送图像数据,串口接收模块接收图像数据并通过模块内部的FIFO存储数据;串并转换模块将串口接收模块存储的图像数据并行输出给PCNN模块,等待处理;PCNN模块接收到图像数据后,开始进行迭代,并输出给VGA显示模块;VGA显示模块负责显示图像经PCNN模块处理后的二值序列,以观察PCNN的处理效果。由于本实验采用的FPGA实验平台提供的时钟频率为50 MHz,而串口接收模块、PCNN模块和VGA显示模块需要特定的时钟频率才能工作,所以必须设计时钟分频模块以产生满足要求的时钟频率。
3 系统仿真
由于考虑边缘神经元的特殊情况,设计了3种略有差异的神经元,即周围神经元输入分别为2、3和4的神经元。这里仅选取4输入的PCNN神经元进行仿真,神经元的阈值为200以验证神经元功能的正确性。通过选取了4个典型的图像灰度值S输入,分别为4、100、200和250,经仿真验证了单个神经元的正确性。
利用单个PCNN神经元,构建了包含9个PCNN神经元PCNN模块,能处理3×3大小的图像,通过网络迭代,得到理想的图像。通过串口输入数据:181、187、140、120、120、4、46、83、120,对PCNN模块进行了仿真。为了便于观察,选取其中3个神经元的时序仿真结果,如图3所示。由图3知,PCNN输出呈现0和1的不断变化,且能看出3个神经元中由于耦合效应产生了不同的结果。图3中S1~S3为9个像素灰度值的3个输入,Y1~Y3为图像经PCNN处理后3个二值序列值。
4 系统验证与分析
本实验以Altera Cyclone II开发平台为验证环境,选用Cyclone系列中的EP2C35F672芯片。利用串口软件发送网像数据,FPGA经PCNN处理后将二值结果显示在VGA显示器上。PCNN模块的时钟输入频率为100MHz,VGA显示模块的时钟输入频率为25 MHz。对于波特率,考虑到已经完成的串口接收模块,选取波特率115 200 bps,以匹配串口接收模块
的采样频率。数据位有8位,无检验位,包含1位停止位,传输数据以16进制的形式进行发送。
为了便于观察,考虑到显示器的刷新频率和人眼的视觉暂留,将PCNN网络的迭代处理频率设定为1 Hz,即显示器每1秒显示一次迭代效果图。图4为显示器前40次的显示效果。图中九宫格代表要处理的3×3输出图像,一个方格代表一个像素点。九宫格中灰色方框神经元点火,即输出为“1”。黑色方框代表神经元未点火,即输出为“0”。
据实验平台的测试结果,与除去VGA模块的硬件模块ModelSim仿真结果进行了对比。图5为除去VGA模块的硬件模块的功能仿真图。图中高电平代表“1”,低电平代表“0”。
果完全符合,这也验证了PCNN网络硬件实现的正确性。此外,由图4和图5看出,神经元1、2、3、4、5、8、9在几次迭代后输出始终为“1”,这是由于神经元的内部活动项始终大于阈值。而由于神经元6和7的图像输入值较小,内部活动项部分和阈值部分不断变化,使得在周围神经元的作用下,呈现周期性的“0”和“1”输出。
5 结论
本文根据脉冲耦合神经网络具有并行计算的特点,提出了一种基于FPGA的神经网络硬件实现方案。利用Verilog硬件描述语言完成了系统模块的设计,构建的PCNN神经网络
在FPGA开发平台上进行了验证。通过处理简单的3x3图像,并观察VGA显示结果,完成了PCNN的FPGA实现,达到了设计要求,图像处理实时性较好。下一步将研究构建更复杂的PCNN网络结构,以处理更大的图像数据。
 电子发烧友App
电子发烧友App























评论