机器学习(Machine Learning, ML)是一门多领域交叉学科,涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。专门研究计算机怎样模拟或实现人类的学习行为,以获取新的知识或技能,重新组织已有的知识结构使之不断改善自身的性能。
严格的定义:机器学习是一门研究机器获取新知识和新技能,并识别现有知识的学问。这里所说的“机器”,指的就是计算机,电子计算机,中子计算机、光子计算机或神经计算机等等。
机器学习概论
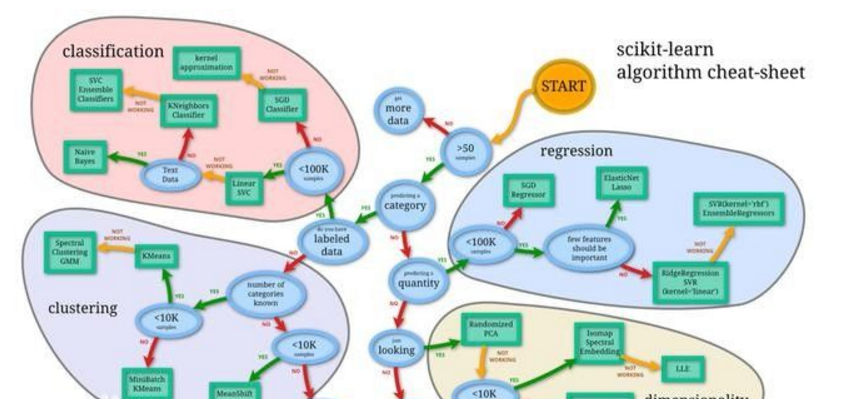
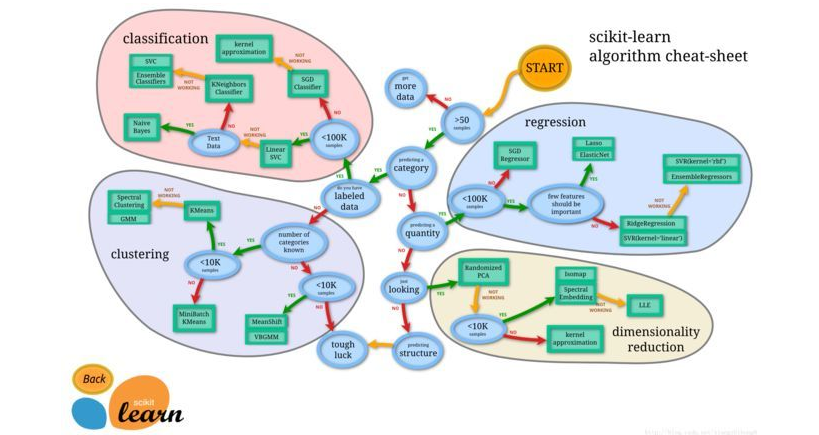
机器学习分为四大块: classification (分类), clustering (聚类), regression (回归), dimensionality reduction (降维)。
classification & regression
举一个简单的例子:
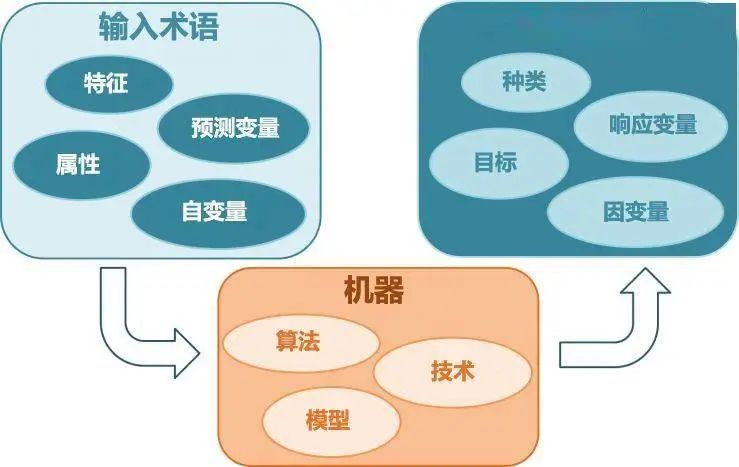
给定一个样本特征 x, 我们希望预测其对应的属性值 y, 如果 y 是离散的, 那么这就是一个分类问题,反之,如果 y 是连续的实数, 这就是一个回归问题。
如果给定一组样本特征 S={x∈RD}, 我们没有对应的 y, 而是想发掘这组样本在 D 维空间的分布, 比如分析哪些样本靠的更近,哪些样本之间离得很远, 这就是属于聚类问题。
如果我们想用维数更低的子空间来表示原来高维的特征空间, 那么这就是降维问题。
无论是分类还是回归,都是想建立一个预测模型 H,给定一个输入 x, 可以得到一个输出 y:
y=H(x)
不同的只是在分类问题中, y 是离散的; 而在回归问题中 y 是连续的。所以总得来说,两种问题的学习算法都很类似。所以在这个图谱上,我们看到在分类问题中用到的学习算法,在回归问题中也能使用。分类问题最常用的学习算法包括 SVM (支持向量机) , SGD (随机梯度下降算法), Bayes (贝叶斯估计), Ensemble, KNN 等。而回归问题也能使用 SVR, SGD, Ensemble 等算法,以及其它线性回归算法。
clustering
聚类也是分析样本的属性, 有点类似classification, 不同的就是classification 在预测之前是知道 y 的范围, 或者说知道到底有几个类别, 而聚类是不知道属性的范围的。所以 classification 也常常被称为 supervised learning, 而clustering就被称为 unsupervised learning。
clustering 事先不知道样本的属性范围,只能凭借样本在特征空间的分布来分析样本的属性。这种问题一般更复杂。而常用的算法包括 k-means (K-均值), GMM (高斯混合模型) 等。
dimensionality reduction
降维是机器学习另一个重要的领域, 降维有很多重要的应用, 特征的维数过高, 会增加训练的负担与存储空间, 降维就是希望去除特征的冗余, 用更加少的维数来表示特征。 降维算法最基础的就是PCA了, 后面的很多算法都是以PCA为基础演化而来。
机器 学习常见算法
机器学习领域涉及到很多的算法和模型,这里遴选一些常见的算法:
正则化算法(Regularization Algorithms)
集成算法(Ensemble Algorithms)
决策树算法(Decision Tree Algorithm)
回归(Regression)
人工神经网络(Artificial Neural Network)
深度学习(Deep Learning)
支持向量机(Support Vector Machine)
降维算法(Dimensionality Reduction Algorithms)
聚类算法(Clustering Algorithms)
基于实例的算法(Instance-based Algorithms)
贝叶斯算法(Bayesian Algorithms)
关联规则学习算法(Association Rule Learning Algorithms)
图模型(Graphical Models)
正则化算法(Regularization Algorithms)
正则化算法是另一种方法(通常是回归方法)的拓展,这种方法会基于模型复杂性对其进行惩罚,它喜欢相对简单能够更好的泛化的模型。
正则化中我们将保留所有的特征变量,但是会减小特征变量的数量级(参数数值的大小θ(j))。这个方法非常有效,当我们有很多特征变量时,其中每一个变量都能对预测产生一点影响。
算法实例:
- 岭回归(Ridge Regression)
- 最小绝对收缩与选择算子(LASSO)
- GLASSO
- 弹性网络(Elastic Net)
- 最小角回归(Least-Angle Regression)
集成算法(Ensemble algorithms)
集成方法是由多个较弱的模型集成模型组,其中的模型可以单独进行训练,并且它们的预测能以某种方式结合起来去做出一个总体预测。这类算法又称元算法(meta-algorithm)。最常见的集成思想有两种bagging和boosting。
boosting
基于错误提升分类器性能,通过集中关注被已有分类器分类错误的样本,构建新分类器并集成。
bagging
基于数据随机重抽样的分类器构建方法。
算法实例:
Boosting
Bootstrapped Aggregation(Bagging)
AdaBoost
层叠泛化(Stacked Generalization)(blending)
梯度推进机(Gradient Boosting Machines,GBM)
梯度提升回归树(Gradient Boosted Regression Trees,GBRT)
随机森林(Random Forest)
总结:当先最先进的预测几乎都使用了算法集成。它比使用单个模型预测出来的结果要精确的多。但是该算法需要大量的维护工作。
决策树算法(Decision Tree Algorithm)
决策树学习使用一个决策树作为一个预测模型,它将对一个 item(表征在分支上)观察所得映射成关于该 item 的目标值的结论(表征在叶子中)。
决策树通过把实例从艮节点排列到某个叶子结点来分类实例,叶子结点即为实例所属的分类。树上的每一个结点指定了对实例的某个属性的测试,并且该结点的每一个后继分支对应于该属性的一个可能值。分类实例的方法是从这棵树的根节点开始,测试这个结点的属性,然后按照给定实例的属性值对应的树枝向下移动。然后这个过程在以新结点的根的子树上重复。
算法实例:
- 分类和回归树(Classification and Regression Tree,CART)
- Iterative Dichotomiser 3(ID3)
- C4.5 和 C5.0(一种强大方法的两个不同版本)
回归(Regression)算法
回归是用于估计两种变量之间关系的统计过程。当用于分析因变量和一个 多个自变量之间的关系时,该算法能提供很多建模和分析多个变量的技巧。具体一点说,回归分析可以帮助我们理解当任意一个自变量变化,另一个自变量不变时,因变量变化的典型值。最常见的是,回归分析能在给定自变量的条件下估计出因变量的条件期望。
算法实例:
普通最小二乘回归(Ordinary Least Squares Regression,OLSR)
线性回归(Linear Regression)
逻辑回归(Logistic Regression)
逐步回归(Stepwise Regression)
多元自适应回归样条(Multivariate Adaptive Regression Splines,MARS)
本地散点平滑估计(Locally Estimated Scatterplot Smoothing,LOESS)
人工神经网络
人工神经网络是受生物神经网络启发而构建的算法模型。它是一种模式匹配,常被用于回归和分类问题,但拥有庞大的子域,由数百种算法和各类问题的变体组成。
人工神经网络(ANN)提供了一种普遍而且实际的方法从样例中学习值为实数、离散值或向量函数。人工神经网络由一系列简单的单元相互连接构成,其中每个单元有一定数量的实值输入,并产生单一的实值输出。
算法实例:
感知器
反向传播
Hopfield 网络
径向基函数网络(Radial Basis Function Network,RBFN)
深度学习(Deep Learning)
深度学习是人工神经网络的最新分支,它受益于当代硬件的快速发展。
众多研究者目前的方向主要集中于构建更大、更复杂的神经网络,目前有许多方法正在聚焦半监督学习问题,其中用于训练的大数据集只包含很少的标记。
算法实例:
深玻耳兹曼机(Deep Boltzmann Machine,DBM)
Deep Belief Networks(DBN)
卷积神经网络(CNN)
Stacked Auto-Encoders
支持向量机(Support Vector Machines)
支持向量机是一种监督式学习 (Supervised Learning)的方法,主要用在统计分类 (Classification)问题和回归分析 (Regression)问题上。支持向量机属于一般化线性分类器,也可以被认为是提克洛夫规范化(Tikhonov Regularization)方法的一个特例。这族分类器的特点是他们能够同时最小化经验误差与最大化几何边缘区,因此支持向量机也被称为最大边缘区分类器。现在多简称为SVM。
给定一组训练事例,其中每个事例都属于两个类别中的一个,支持向量机(SVM)训练算法可以在被输入新的事例后将其分类到两个类别中的一个,使自身成为非概率二进制线性分类器。
SVM 模型将训练事例表示为空间中的点,它们被映射到一幅图中,由一条明确的、尽可能宽的间隔分开以区分两个类别。
降维算法(Dimensionality Reduction Algorithms)
所谓的降维就是指采用某种映射方法,将原高维空间中的数据点映射到低维度的空间中。降维的本质是学习一个映射函数 f : x-》y,其中x是原始数据点的表达,目前最多使用向量表达形式。 y是数据点映射后的低维向量表达,通常y的维度小于x的维度(当然提高维度也是可以的)。f可能是显式的或隐式的、线性的或非线性的。
这一算法可用于可视化高维数据或简化接下来可用于监督学习中的数据。许多这样的方法可针对分类和回归的使用进行调整。
算法实例:
主成分分析(Principal Component Analysis (PCA))
主成分回归(Principal Component Regression (PCR))
偏最小二乘回归(Partial Least Squares Regression (PLSR))
Sammon 映射(Sammon Mapping)
多维尺度变换(Multidimensional Scaling (MDS))
投影寻踪(Projection Pursuit)
线性判别分析(Linear Discriminant Analysis (LDA))
混合判别分析(Mixture Discriminant Analysis (MDA))
二次判别分析(Quadratic Discriminant Analysis (QDA))
灵活判别分析(Flexible Discriminant Analysis (FDA))
聚类算法(Clustering Algorithms)
聚类算法是指对一组目标进行分类,属于同一组(亦即一个类,cluster)的目标被划分在一组中,与其他组目标相比,同一组目标更加彼此相似。
优点是让数据变得有意义,缺点是结果难以解读,针对不同的数据组,结果可能无用。
算法实例:
K-均值(k-Means)
k-Medians 算法
Expectation Maximi 封层 ation (EM)
最大期望算法(EM)
分层集群(Hierarchical Clstering)
贝叶斯算法(Bayesian Algorithms)
贝叶斯定理(英语:Bayes’ theorem)是概率论中的一个定理,它跟随机变量的条件概率以及边缘概率分布有关。在有些关于概率的解说中,贝叶斯定理(贝叶斯更新)能够告知我们如何利用新证据修改已有的看法。贝叶斯方法是指明确应用了贝叶斯定理来解决如分类和回归等问题的方法。
算法实例:
朴素贝叶斯(Naive Bayes)
高斯朴素贝叶斯(Gaussian Naive Bayes)
多项式朴素贝叶斯(Multinomial Naive Bayes)
平均一致依赖估计器(Averaged One-Dependence Estimators (AODE))
贝叶斯信念网络(Bayesian Belief Network (BBN))
贝叶斯网络(Bayesian Network (BN))
关联规则学习算法(Association Rule Learning Algorithms)
关联规则学习方法能够提取出对数据中的变量之间的关系的最佳解释。比如说一家超市的销售数据中存在规则 {洋葱,土豆}=》 {汉堡},那说明当一位客户同时购买了洋葱和土豆的时候,他很有可能还会购买汉堡肉。有点类似于联想算法。
算法实例:
Apriori 算法(Apriori algorithm)
Eclat 算法(Eclat algorithm)
FP-growth
图模型(Graphical Models)
图模型(GraphicalModels)在概率论与图论之间建立起了联姻关系。它提供了一种自然工具来处理应用数学与工程中的两类问题——不确定性(Uncertainty)和复杂性(Complexity)问 题,特别是在机器学习算法的分析与设计中扮演着重要角色。图模型的基本理念是模块化的思想,复杂系统是通过组合简单系统建构的。概率论提供了一种粘合剂使 系统的各个部分组合在一起,确保系统作为整体的持续一致性,提供了多种数据接口模型方法。
图模型或概率图模型(PGM/probabilistic graphical model)是一种概率模型,一个图(graph)可以通过其表示随机变量之间的条件依赖结构(conditional dependence structure)。
算法实例:
贝叶斯网络(Bayesian network)
马尔可夫随机域(Markov random field)
链图(Chain Graphs)
祖先图(Ancestral graph)
责任编辑:Ct
 电子发烧友App
电子发烧友App




















评论