以下是关于Rahul Agarwal 分享的内容,编译整理如下。
数据科学实际上是就是研究算法。
我每天都在努力学习许多算法,所以我想列出一些最常见和最常用的算法。
本文介绍了在处理数据时可以使用的一些最常见的采样技术。
简单随机抽样
假设您要选择一个群体的子集,其中该子集的每个成员被选择的概率都相等。
下面我们从一个数据集中选择 100 个采样点。
sample_df = df.sample(100)
分层采样
假设我们需要估计选举中每个候选人的平均票数。现假设该国有 3 个城镇:
A 镇有 100 万工人,
B 镇有 200 万工人,以及
C 镇有 300 万退休人员。
我们可以选择在整个人口中随机抽取一个 60 大小的样本,但在这些城镇中,随机样本可能不太平衡,因此会产生偏差,导致估计误差很大。
相反,如果我们选择从 A、B 和 C 镇分别抽取 10、20 和 30 个随机样本,那么我们可以在总样本大小相同的情况下,产生较小的估计误差。
使用 python 可以很容易地做到这一点:
from sklearn.model_selection import train_test_splitX_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, test_size=0.25)
水塘采样
我喜欢这个问题陈述:
假设您有一个项目流,它长度较大且未知以至于我们只能迭代一次。
创建一个算法,从这个流中随机选择一个项目,这样每个项目都有相同的可能被选中。
我们怎么能做到这一点?
假设我们必须从无限大的流中抽取 5 个对象,且每个元素被选中的概率都相等。
import randomdef generator(max):
number = 1
while number 《 max:
number += 1
yield number# Create as stream generator
stream = generator(10000)# Doing Reservoir Sampling from the stream
k=5
reservoir = []
for i, element in enumerate(stream):
if i+1《= k:
reservoir.append(element)
else:
probability = k/(i+1)
if random.random() 《 probability:
# Select item in stream and remove one of the k items already selected
reservoir[random.choice(range(0,k))] = elementprint(reservoir)
------------------------------------
[1369, 4108, 9986, 828, 5589]
从数学上可以证明,在样本中,流中每个元素被选中的概率相同。这是为什么呢?
当涉及到数学问题时,从一个小问题开始思考总是有帮助的。
所以,让我们考虑一个只有 3 个项目的流,我们必须保留其中 2 个。
当我们看到第一个项目,我们把它放在清单上,因为我们的水塘有空间。在我们看到第二个项目时,我们把它放在列表中,因为我们的水塘还是有空间。
现在我们看到第三个项目。这里是事情开始变得有趣的地方。我们有 2/3 的概率将第三个项目放在清单中,
现在让我们看看第一个项目被选中的概率:
移除第一个项目的概率是项目 3 被选中的概率乘以项目 1 被随机选为水塘中 2 个要素的替代候选的概率。这个概率是:
2/3*1/2 = 1/3
因此,选择项目 1 的概率为:
1–1/3=2/3
我们可以对第二个项目使用完全相同的参数,并且可以将其扩展到多个项目。
因此,每个项目被选中的概率相同:2/3 或者用一般的公式表示为 K/N
随机欠采样和过采样
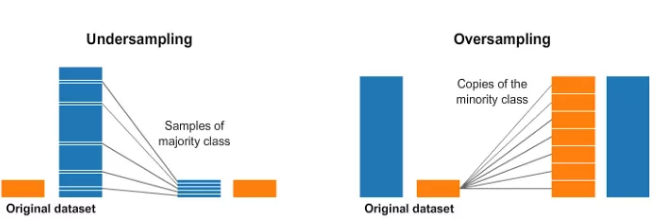
我们经常会遇到不平衡的数据集。
一种广泛采用的处理高度不平衡数据集的技术称为重采样。它包括从多数类(欠采样)中删除样本或向少数类(过采样)中添加更多示例。
让我们先创建一些不平衡数据示例,
from sklearn.datasets import make_classificationX, y = make_classification( n_classes=2, class_sep=1.5, weights=[0.9, 0.1], n_informative=3, n_redundant=1, flip_y=0, n_features=20, n_clusters_per_class=1, n_samples=100, random_state=10)X = pd.DataFrame(X)X[ target ] = y
我们现在可以使用以下方法进行随机过采样和欠采样:
num_0 = len(X[X[ target ]==0])num_1 = len(X[X[ target ]==1])print(num_0,num_1)# random undersampleundersampled_data = pd.concat([ X[X[ target ]==0].sample(num_1) , X[X[ target ]==1] ])print(len(undersampled_data))# random oversampleoversampled_data = pd.concat([ X[X[ target ]==0] , X[X[ target ]==1].sample(num_0, replace=True) ])print(len(oversampled_data))------------------------------------------------------------OUTPUT:90 1020180
使用 imbalanced-learn 进行欠采样和过采样
imbalanced-learn(imblearn)是一个用于解决不平衡数据集问题的 python 包,它提供了多种方法来进行欠采样和过采样。
a. 使用 Tomek Links 进行欠采样:
imbalanced-learn 提供的一种方法叫做 Tomek Links。Tomek Links 是邻近的两个相反类的例子。
在这个算法中,我们最终从 Tomek Links 中删除了大多数元素,这为分类器提供了一个更好的决策边界。
from imblearn.under_sampling import TomekLinks
tl = TomekLinks(return_indices=True, ratio= majority )
X_tl, y_tl, id_tl = tl.fit_sample(X, y)
b. 使用 SMOTE 进行过采样:
在 SMOE(Synthetic Minority Oversampling Technique)中,我们在现有元素附近合并少数类的元素。
from imblearn.over_sampling import SMOTE
smote = SMOTE(ratio= minority )
X_sm, y_sm = smote.fit_sample(X, y)
imbLearn 包中还有许多其他方法,可以用于欠采样(Cluster Centroids, NearMiss 等)和过采样(ADASYN 和 bSMOTE)。
结论
算法是数据科学的生命线。
抽样是数据科学中的一个重要课题,但我们实际上并没有讨论得足够多。
有时,一个好的抽样策略会大大推进项目的进展。错误的抽样策略可能会给我们带来错误的结果。因此,在选择抽样策略时应该小心。
 电子发烧友App
电子发烧友App



























评论