相机标定内参和外参
在图像测量过程以及机器视觉应用中,为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系,必须建立相机成像的几何模型,这些几何模型参数就是相机参数。在大多数条件下这些参数必须通过实验与计算才能得到,这个求解参数的过程就称之为相机标定(或摄像机标定)。无论是在图像测量或者机器视觉应用中,相机参数的标定都是非常关键的环节,其标定结果的精度及算法的稳定性直接影响相机工作产生结果的准确性,做好相机标定和提高标定精度是做好后续工作的前提。
相机标定中所要确定的几何模型参数分为内参和外参两种类型。相机内参的作用是确定相机从三维空间到二维图像的投影关系。相机外参的作用是确定相机坐标与世界坐标系之间相对位置关系。
相机内参共有6个参数(f,κ,Sx,Sy,Cx,Cy),其中:
f为焦距;
κ表示径向畸变量级,如果κ为负值,畸变为桶型畸变,如果为正值,那畸变为枕型畸变。
Sx,Sy是缩放比例因子。一般情况下相机成像单元不是严格的矩形的,其在水平和垂直方向上的大小是不一致的,这就导致在X和Y方向上的缩放因子不一样,所以需要分别定义两个缩放因子。对针孔摄像机来讲,表示图像传感器上水平和垂直方向上相邻像素之间的距离;
Cx,Cy是图像的主点,即过镜头轴心垂直于成像平面与图像平面的交点。对针孔摄像机来讲,这个点是投影中心在成像平面上的垂直投影,同时也是径向畸变的中心 。
摄像机外参共有6个参数(α,β,γ,Tx,Ty,Tz),相机坐标与世界坐标的关系可以表述为:
Pc= RPw + T
其中Pw为世界坐标,Pc是摄像机坐标。式中,T= (Tx,Ty,Tz),是平移向量,R =R(α,β,γ)是旋转矩阵,分别是绕摄像机坐标系z轴旋转角度为γ,绕y轴旋转角度为β,绕x轴旋转角度为α。6个参数组成(α,β,γ,Tx,Ty,Tz)为摄像机外参。
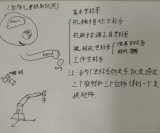
通常情况下,通过镜头,一个三维空间中的物体会被映射成一个倒立缩小的像,然后被成像传感器感知到。
●理想情况下,镜头的光轴(就是通过镜头中心垂直于传感器平面的直线)应该是穿过图像的正中间的,但是,实际由于安装精度的问题,总是存在误差,即光轴偏移,这种误差需要用内参来描述;
●理想情况下,相机对x方向和y方向的尺寸的缩小比例是一样的,但实际上,镜头如果不是完美的圆,传感器上的像素如果不是完美的紧密排列的正方形,都可能会导致这两个方向的缩小比例不一致。内参中包含两个参数可以描述这两个方向的缩放比例,不仅可以将用像素数量来衡量的长度转换成三维空间中的用其它单位(比如米)来衡量的长度,也可以表示在x和y方向的尺度变换的不一致性;
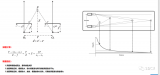
●理想情况下,镜头会将一个三维空间中的直线也映射成直线(即射影变换),但实际上,镜头无法这么完美,通过镜头映射之后,直线会变弯,所以需要相机的畸变参数来描述这种变形效果。以下三种畸变分别为枕形畸变、桶形畸变和线性畸变。



相机标定的方法
相机标定方法有:传统相机标定法、相机自标定法、主动视觉相机标定方法。
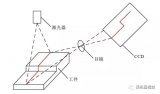
传统相机标定法需要使用尺寸已知的标定物,通过建立标定物上坐标已知的点与其图像点之间的对应,利用一定的算法获得相机模型的内外参数。根据标定物的不同可分为三维标定物和平面型标定物。三维标定物可由单幅图像进行标定,标定精度较高,但高精密三维标定物的加工和维护较困难。平面型标定物比三维标定物制作简单,精度易保证,但标定时必须采用两幅或两幅以上的图像。传统相机标定法在标定过程中始终需要标定物,且标定物的制作精度会影响标定结果。同时有些场合不适合放置标定物也限制了传统相机标定法的应用。
传统的相机标定方法的优点是可以使用于任意的摄像机模型,标定精度高,缺点是标定过程复杂,需要高精度的标定模板,在一些场合下无法使用标定块。
目前出现的自标定算法中主要是利用相机运动的约束。相机的运动约束条件太强,因此使得其在实际中并不实用。利用场景约束主要是利用场景中的一些平行或者正交的信息。其中空间平行线在相机图像平面上的交点被称为消失点,它是射影几何中一个非常重要的特征,所以很多学者研究了基于消失点的相机自标定方法。自标定方法灵活性强,可对相机进行在线定标。但由于它是基于绝对二次曲线或曲面的方法,其算法鲁棒性差。仅仅依靠多幅图像之间的对应关系进行标定,优点是仅需要建立图像之间的对应,灵活性强,潜在应用范围广,缺点是非线性标定,鲁棒性不高。
基于主动视觉的相机标定法是指已知相机的某些运动信息对相机进行标定。该方法不需要标定物,但需要控制相机做某些特殊运动,利用这种运动的特殊性可以计算出相机内部参数。基于主动视觉的相机标定法的优点是算法简单,往往能够获得线性解,故鲁棒性较高,缺点是系统的成本高、实验设备昂贵、实验条件要求高,而且不适合于运动参数位置或无法控制的场合。
主动视觉相机标定方法应用的前提是已知相机的某些运动信息,优点是可以线性求解,鲁棒性较好,缺点是不能使用与相机运动信息未知和无法控制相机运动的场合。
标定模板
标定模板(标定板 Calibration Target) 在机器视觉、图像测量、摄影测量、三维重建等应用中,为校正镜头畸变;确定物理尺寸和像素间的换算关系;以及确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系,需要建立相机成像的几何模型。通过相机拍摄带有固定间距图案阵列平板、经过标定算法的计算,可以得出相机的几何模型,从而得到高精度的测量和重建结果。而带有固定间距图案阵列的平板就是标定模板(标定板 Calibration Target)。
常见标定模板种类
1)等间距实心圆阵列图案 Ti-times CG-100-D

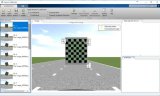
2)国际象棋盘图案 Ti-times CG-076-T

一般需要20张图片,这只是一个经验值,实际上太多也不好,太少也不好。单纯从统计上来看,可能越多会越好,但是,实际上图片太多可能会让参数优化的结果变差,因为棋盘格角点坐标的确定是存在误差的,而且这种误差很难说是符合高斯分布的,同时,标定过程所用的非线性迭代优化算法不能保证总是得到最优解,而更多的图片,可能会增加算法陷入局部最优的可能性。
拍照时的标定板位置和朝向的多样性,会让内参的估计更为准确。准确的内参可以较好地把整个图像的畸变都进行矫正,但如果给定的标定板的位置过于单一,比如都是在图像的左上角,那么优化得到的内参也可能只会比较好地纠正图像左上角的畸变。推荐找个畸变较大的镜头做做实验,会更形象。·
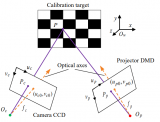
世界坐标系、相机坐标系、图像坐标系
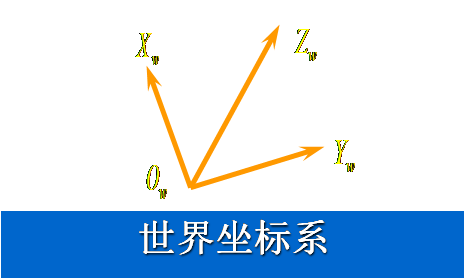
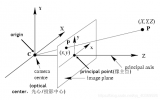
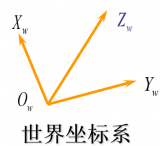
世界坐标系(Xw、Yw、Zw)
是由用户定义的空间三维坐标系,用来描述三维空间中的物体和相机之间的坐标位置,满足右手法则,世界坐标系是物理世界中反映物体位置的真实坐标。
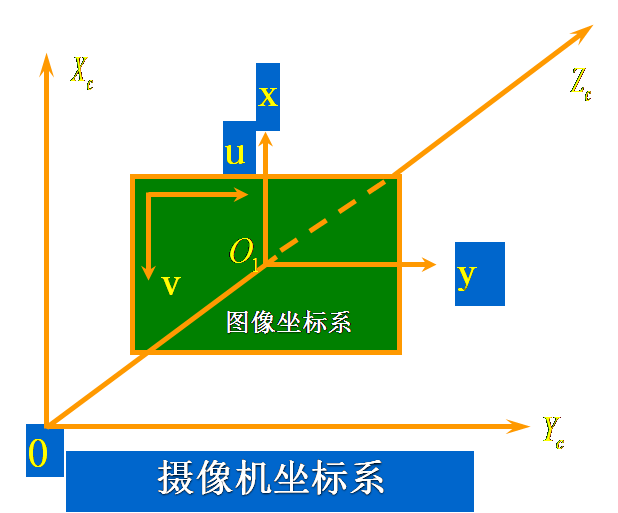
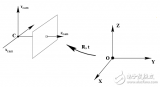
相机坐标系(Xc、Yc、Zc)
以相机的光心作为原点,Zc轴与光轴重合,并垂直于成像平面,且取摄影方向为正方向,Xc、Yc轴与图像物理坐标系的x、y轴平行。
图像坐标系(u、v)或(x、y)
是以图像的左上角为原点的图像坐标系(u,v),以像素为单位,
张正友标定方法
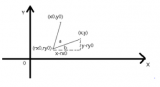
通过在图像上一个二维点m=[u,t]后加上一个1的向量,在相机坐标系中一个3D点M=[X,Y,Z]后也加上一个1的向量,在针孔模型中,3D点M和它的图像投影m的关系为:
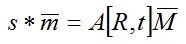
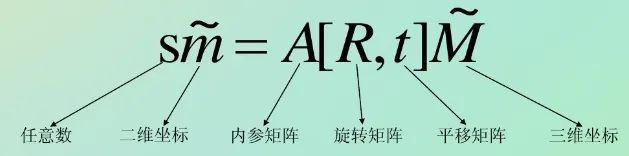
其中内参A为:
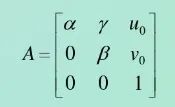
若定义H=A[R,t],有s*m=H*M,则H就是通常说的单应性矩阵,在这里描述的是空间中平面三维点和相机平面二维点之间的关系,相机平面中的坐标点可以通过图像处理寻找角点的方式获取,空间平面三维点可以通过尺寸已知的标定板获取,所以说针对每张图图片都可以计算出来一个对应的H矩阵。
转动标定模板,从不同的角度拍摄棋盘标定模板的n幅图像,求出内参矩阵和外参矩阵,就有了相机坐标和图像坐标的投射矩阵,就可以将空间中的某一点映射到图片上的某一个点上: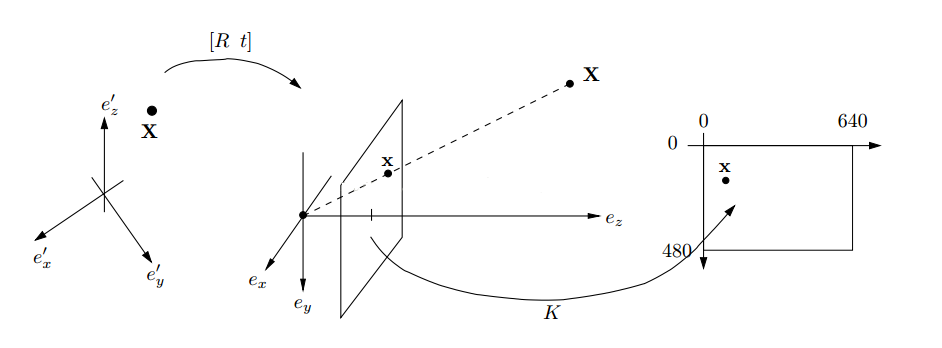
张正友相机标定流程
1. 打印棋盘标定纸,附加到一个平坦的表面上;
2. 通过移动相机或者平面拍摄标定板各种角度的图片,一般拍摄20张;
3. 检测图片中的特征点;
4. 计算5个内部参数和所有的外部参数;
5. 通过最小二乘法先行求解径向畸变系数;
6. 通过求最小参数值,优化所有参数;
张正友的平面标定方法是介于传统标定方法和自标定方法之间的一种方法,它既避免了传统方法设备要求高,操作繁琐等缺点,又较自标定方法精度高,符合通用的桌面视觉系统(DVS)的标定要求。该方法的缺点是确定模板上点阵的物理坐标以及图像和模板之间的点的匹配,专业性要求比较高。
编辑:黄飞
 电子发烧友App
电子发烧友App




























评论