深度解析深度学习的知识蒸馏技术

问题来源

最近读到一篇模型蒸馏的文章 [1]，其中在设计软标签的损失函数时使用了一种特殊的 softmax：  

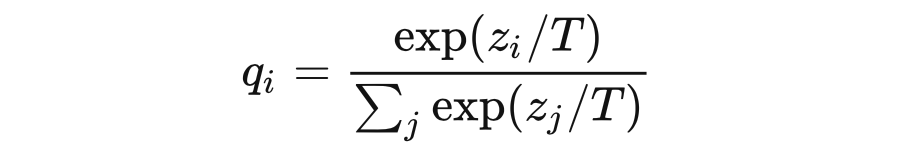
文章中只是简单的提了一下，其中 T 是 softmax 函数的温度超参数，而没有做过多解释。这说明这种用法并非其首创，应该是流传已久。经过一番调研和学习，发现知乎上最高赞的文章《深度学习中的 temperature parameter 是什么》[13] 对超参数 T 的讲解具有很强的误导性，所以在此重新写一篇文章为其正名。   本文的标题有两个双关。一个是知识蒸馏的方法用于深度学习，同时也需要深入学习；另一个则是本文的核心：蒸馏中如何合理运用温度，让隐藏的知识更好地挥发和凝结。下面我将详细讲解以上 softmax 公式中温度系数的由来以及它起到的作用。    

蒸馏模型

模型蒸馏或知识蒸馏，最早在 2006 年由 Buciluǎ 在文章 Model Compression [14] 中提出（很多博主把人名都写错了。其后，Hinton 进行了归纳和发展，并在 2015 年发表了经典之作 Distilling the Knowledge in a Neural Network [15]。正是在这篇文章 [2] 中，Hinton 首次提出了 Softmax with Temperature 的方法。   先简要概括一下模型蒸馏在做什么。出于计算资源的限制或效率的要求，深度学习模型在部署推断时往往需要进行压缩，模型蒸馏是其中一种常见方法。将原始数据集上训练的重量级（cumbersome）模型作为教师，让一个相对更轻量的模型作为学生。   对于相同的输入，让学生输出的概率分布尽可能的逼近教师输出的分布，则大模型的知识就通过这种监督训练的方式「蒸馏」到了小模型里。小模型的准确率往往下降很小，却能大幅度减少参数量，从而降低推断时对 CPU、内存、能耗等资源的需求。   对于传统的监督训练，损失函数可以写为 KL-散度 ，表示用分布 拟合分布 带来的误差。其中 是输出的真实分布，我们的数据集的标签 就从这个分布中采样而来，对于一个 分类问题， 常常会表示为 one-hot 向量，包含 1  个 1 和 个 0。对于模型蒸馏，损失函数可以表示为 ，表示用学生模型的输出 来拟合教师模型的输出 。   我们知道模型在训练收敛后，往往通过 softmax 的输出不会是完全符合 one-hot 向量那种极端分布的，而是在各个类别上均有概率，推断时通过 argmax 取得概率最大的类别。Hinton 的文章就指出，教师模型中在这些负类别（非正确类别）上输出的概率分布包含了一定的隐藏信息。比如 MNIST 手写数字识别，标签为 7 的样本在输出时，类别 7 的概率虽然最大，但和类别 1 的概率更加接近，这就说明 1 和 7 很像，这是模型已经学到的隐藏的知识。   我们在使用 softmax 的时候往往会将一个差别不大的输出变成很极端的分布，用一个三分类模型的输出举例：  

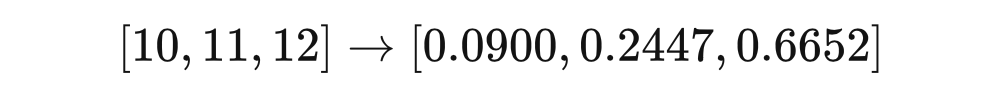
可以看到原本的分布很接近均匀分布，但经过 softmax，不同类别的概率相差很大。这就导致类别间的隐藏的相关性信息不再那么明显，有谁知道 0.09 和 0.24 对应的类别很像呢？为了解决这个问题，我们就引入了温度系数。    

温度系数

我们看看对于随机生成的相同的模型输出，经过不同的函数处理，分布会如何变化：  

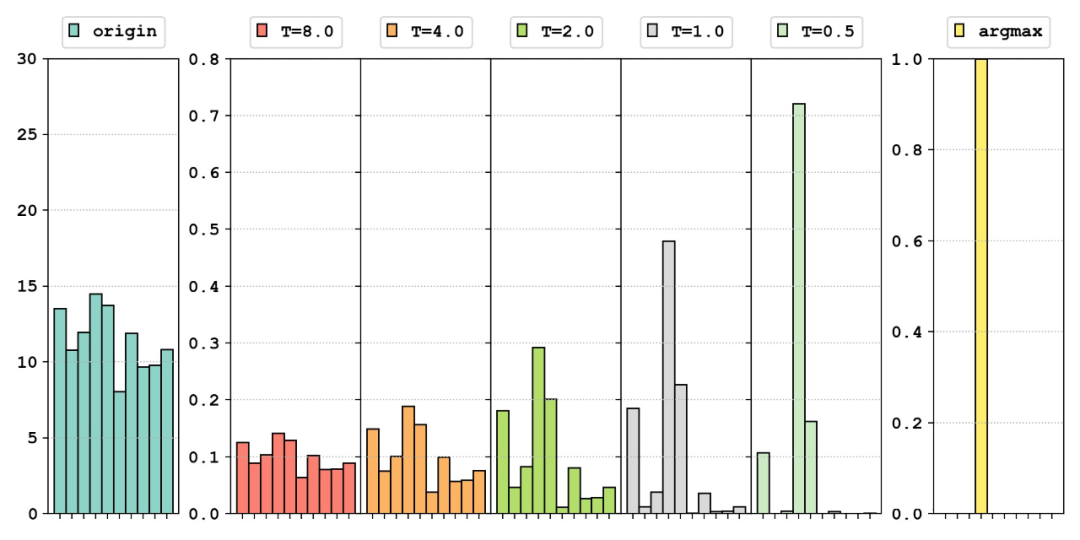
最左边是我们随机生成的分布来模拟模型的输出：。中间五幅图是使用 softmax 得到的结果；其中温度系数 时相当于原始的 softmax；右侧对比了 argmax 得到的结果。可以看出，从左到右，这些输出结果逐渐从均匀分布向尖锐分布过渡，其中保留的除正确类别以外的信息越来越少。下图 [3] 更加直观地展示了不同的温度系数 对输出分布的影响。  

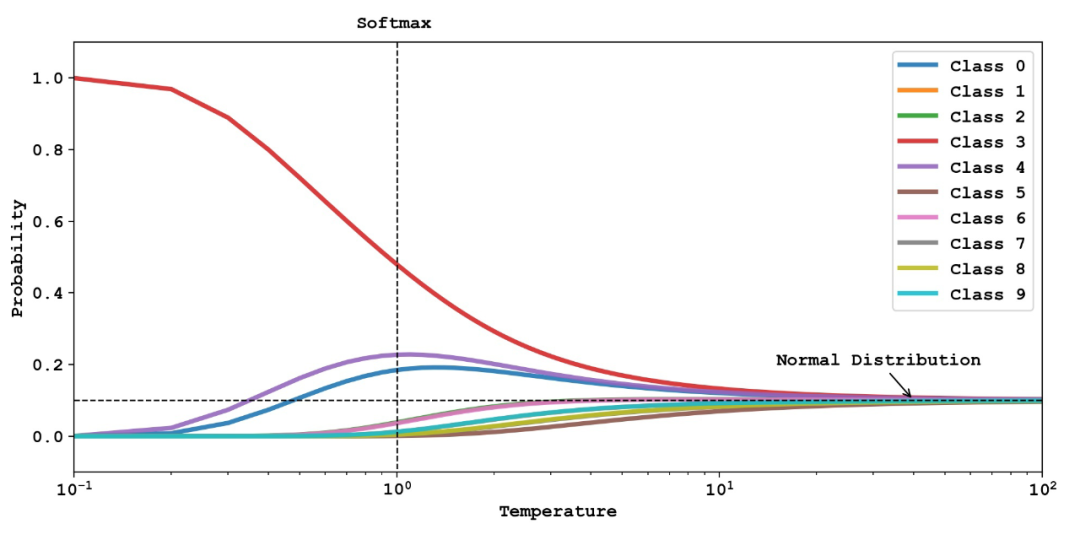
灵感来源：https://www.youtube.com/watch?v=tOItokBZSfU

不同的曲线代表不同类别上的概率输出，同样 时代表传统的 softmax，在 时，分布逐渐极端化，最终等价于 argmax，在 时，分布逐渐趋于均匀分布，10 个类别的概率都趋近于1/10。   这两幅画很好的说明了 softmax 的本质。相对于 argmax 这种直接取最大的「hardmax」，softmax 采用更温和的方式，将正确类别的概率一定程度地突显出来。而引入温度系数的本质目的，就是让 softmax 的 soft 程度变成可以调节的超参数。  

而至于这个系数为啥叫 Temperature，其实很有深意。我们知道这个场景最早用于模型蒸馏，一般来说蒸馏需要加热，而加热会导致熵增。我们发现，提高温度系数会导致输出分布的信息熵增大！[4] 而在 Hinton 的这篇论文里，为了充分利用教师模型负类别的 dark 信息，一般会选用一个较高的温度系数，这也是本文标题叫做高温蒸馏的原因。   我们可以轻松地推导出 趋于无穷大时，分布将趋于均匀分布，此时信息熵趋于最大  

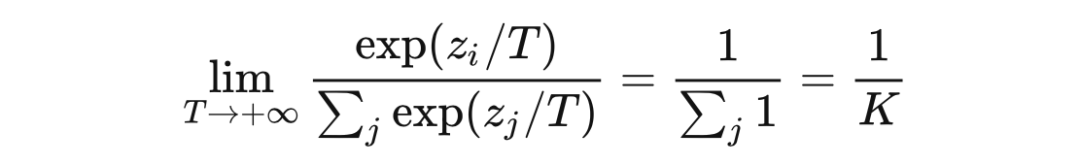
而当 趋于 0 时，正确类别的概率接近 1，softmax 的效果逼近 argmax  

 

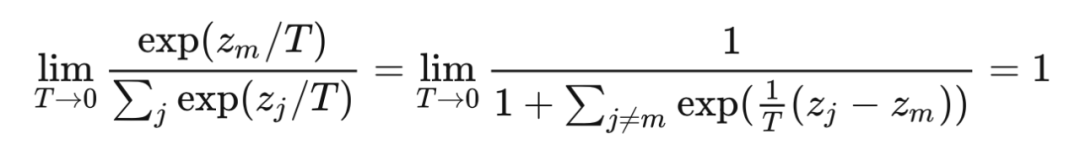
反对意见

在最高赞的那篇文章中提到：

如果我们在训练时将t设置比较大，那么预测的概率分布会比较平滑，那么loss会很大

首先，如果原文考虑的问题中数据的标签是 one-hot 向量而不是蒸馏这种软标签， 较大时 loss 确实会较大，因为输出分布比较均匀，不能很好地凸显正类别上的概率优势。但在蒸馏时并非如此，Hinton 给出的 Loss 函数如下图 [5] 所示，分为两项：  

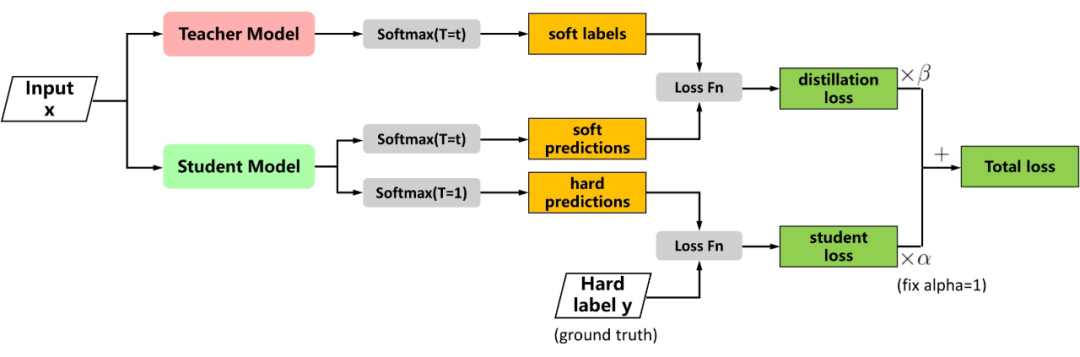
图源：https://nni.readthedocs.io/en/stable/sharings/kd_example.html

第一项  是教师模型与学生模型的输出之间的交叉熵，第二项 是学生模型与真实标签之间的交叉熵。传统训练模型时只有 项，所以 可以看做是引入的正则项。文中指出这个正则项使得学生模型能够学到教师模型中的高度泛化的知识，从而需要更少的真实训练样本。   文中的实验只用了 3% 的训练样本，就达到了近似教师模型的准确率。我们可以看到这里的 项中，两个模型都使用了同样的、较大的温度系数 ，对输出的作用是相同的，未必会使 loss 变大。  

……那么loss会很大，这样可以避免我们陷入局部最优解。

为什么 loss 大就可以避免陷入局部最优呢？我猜作者想表达的是 loss 很大，从而随机梯度下降的时候梯度很大，步长就会很大，从而更容易跳出局部最优。该文章的评论区也有同样的声音，但可惜这并不正确。我们还以硬标签 监督训练为例，使用交叉熵损失函数，设 softmax 的输出为 ，我们可以推导 loss 对于模型输出 的梯度：  

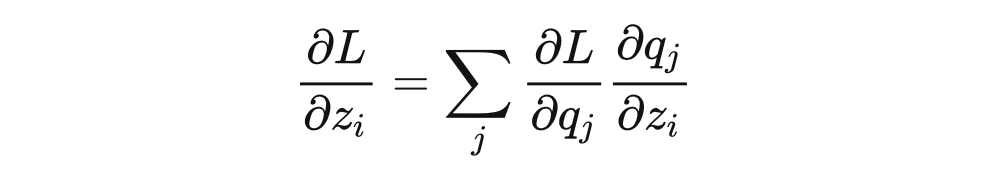
交叉熵的梯度  

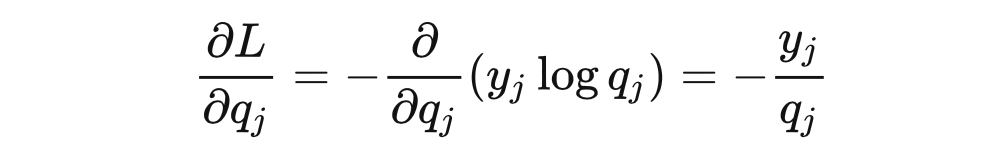
softmax 的梯度  

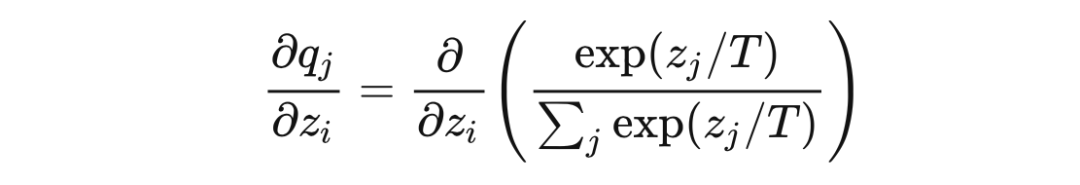
当 时  

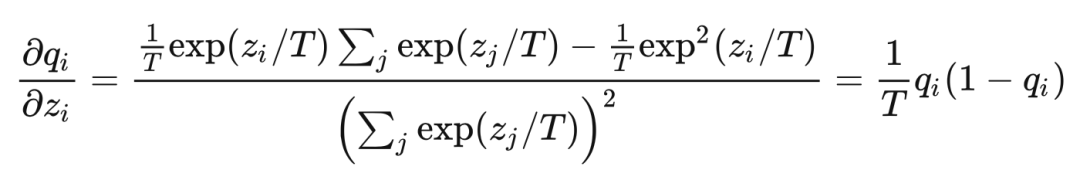
当 时  

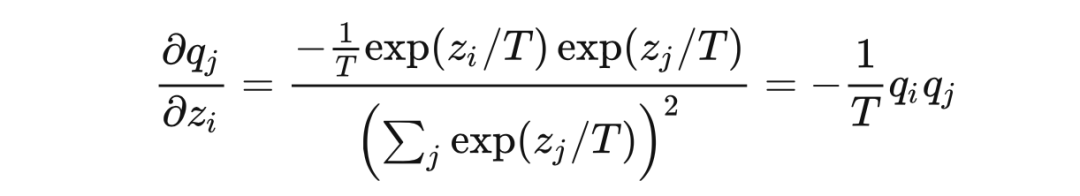
代入链式法则，最终的梯度为（推导参考了 [6][7]）  

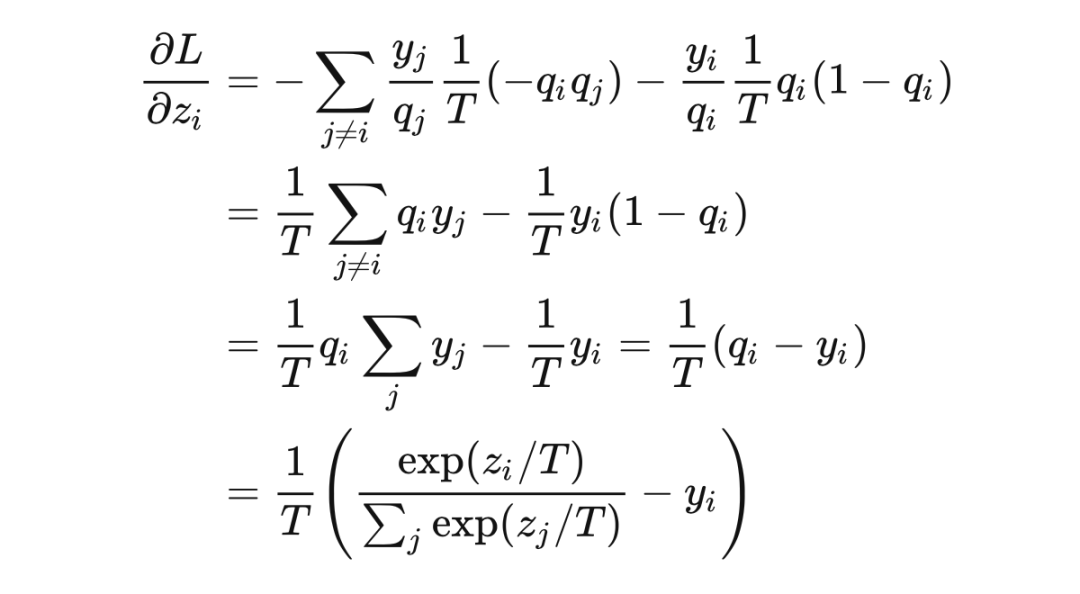
显然标签 与 softmax 的输出 之差不总能增长 倍，大家可以自己举一些反例，会发现大多数情况下，梯度都不是增大的。那么对于 Hinton 这篇论文，由于 loss 的数量级没有变化，所以梯度实际是减小的，所以文章中特意强调了要将系数 设置大一些来补偿，比如设置为 ，在这里给出的 Pytorch 实现 [16] 中也是这么做的。   文章中给出了一个高温情况下的等价，在 时，利用等价无穷小或者是泰勒展开得到：  

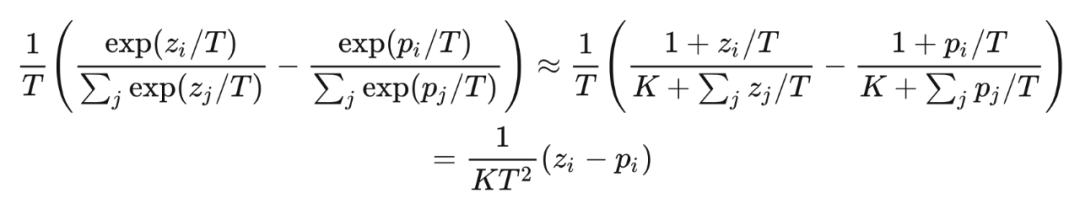
可以清晰的看出这里是 的关系。  

随着训练的进行，我们将 t 变小，也可以称作降温，类似于模拟退火算法，这也是为什么要把 t 称作温度参数的原因。变小模型才能收敛。

我不知道将这里的温度系数类比模拟退火算法的温度系数有什么依据（Quora 上有个类似的 [8]），但它们真的是不怎么像。同样也未必是温度系数变小模型才能收敛，需要分情况：如果是模型蒸馏， 项始终都使用较大的温度；如果是使用真实标签训练，确实选取较小的温度系数，更利于模型收敛。   可以这样理解，温度系数较大时，模型需要训练得到一个很陡峭的输出，经过 softmax 之后才能获得一个相对陡峭的结果；温度系数较小时，模型输出稍微有点起伏，softmax 就很敏感地把分布变得尖锐，认为模型学到了知识。   所以，使用一个固定的小于 1 的温度系数是合理的，这也是那篇文章里提到的推荐系统所做的，它没有降温过程，直接设置了 T=0.05 。如果大家在哪篇文章中看到了降温过程，还请在评论区指正。    

其他场景

  这里我们天马行空地设想一个场景：在一些序列生成任务中，比如 seq2seq 的机器翻译模型，或者是验证码识别的 CTC 算法 [9] 中，输出的每一个时间步都会有一个分布。最终的序列会使用 BeamSearch [10] 或者 Viterbi [11] 等算法搜索 Top-K 概率的序列。   这类方法介于逐时间步 argmax 的完全贪心策略和全局动态规划的优化策略之间。虽然 BeamSearch 中我们不需要提前 softmax，但假如我们做了带温度系数的 softmax，就可以控制输出分布的尖锐程度。对于这类逐步计算累积概率的算法，在每个时间步的概率分布较为均匀时就容易输出不同的结果。所以在这类问题下，高温可能导致输出序列的多样性。   对于这类场景，我没有进行严格证明也没有很深的经验，只是一个猜想。这里有类似的说法 [12]，但都不能作为参考依据。大家感兴趣的话可以将 softmax with temperature 引入 BeamSearch 看看会不会对输出的丰富性造成影响。假如算法只依赖每个时间步的概率大小关系，那输出就是确定的，说明我们猜想失败。或者有相关经验的同学也可以在评论区给出参考文献。    

后话

写完这篇文章才发现，潘小小【经典简读】知识蒸馏（Knowledge Distillation）经典之作 [17] 一文中已有类似的探讨。尽管如此，我相信这篇文章还是可以起到一定的科普作用，让那些和我一样对知识蒸馏不太了解的同学，从温度系数这个关键词入手，能够快速得到想要的答案。   读完 Hinton 的文章，有两个强烈的感受：一是感觉他太牛了，3 句话让我读了  18 遍，全文很少用公式，基本没有配图，但把算法讲得清清楚楚；二就是，他的写作中长从句实在太多了，一句话 60 个单词，读起来很不友好。如果对这篇文章感兴趣，也可以看上面潘小小的那篇解读。文章最后讲到了一种和 MOE 很像的分布式集成学习方法，在潘的文章中没有介绍，由于这不是今天的主题，所以我也没用笔墨，大家如果对这部分感兴趣也可以来找我讨论。   说出来很难相信，我其实不是做 AI 方向的，我是做系统的，所以欢迎大家怼我（°ー°〃）。      

参考文献

[1] Group knowledge transfer: Federated learning of large cnns at the edgehttps://proceedings.neurips.cc/paper/2020/file/a1d4c20b182ad7137ab3606f0e3fc8a4-Paper.pdf

[2]Distilling the Knowledge in a Neural Network https://arxiv.org/abs/1503.02531

[3] PR-009: Distilling the Knowledge in a Neural Network (Slide: English, Speaking: Korean) https://www.youtube.com/watch?v=tOItokBZSfU

[4] What is the role of temperature in Softmax?https://stats.stackexchange.com/questions/527080/what-is-the-role-of-temperature-in-softmax#answer-527082

[5] Knowledge Distillation on NNIhttps://nni.readthedocs.io/en/stable/sharings/kd_example.html

[6] softmax, CrossEntropyLoss 与梯度计算公式https://blog.csdn.net/jiongjiongai/article/details/88324000

[7] 关于Softmax的数值稳定性和梯度反向传播https://zhuanlan.zhihu.com/p/92714192

[8] What is the temperature parameter in deep learning?https://www.quora.com/What-is-the-temperature-parameter-in-deep-learning

[9] 详解CTChttps://zhuanlan.zhihu.com/p/42719047

[10] 文本生成解码之 Beam Searchhttps://zhuanlan.zhihu.com/p/43703136

[11] 如何通俗地讲解 viterbi 算法？https://www.zhihu.com/question/20136144/answer/763021768

[12]What is Temperature in LSTM? https://www.quora.com/What-is-Temperature-in-LSTM

[13] https://zhuanlan.zhihu.com/p/132785733 

[14] https://dl.acm.org/doi/abs/10.1145/1150402.1150464 

[15] https://arxiv.org/abs/1503.02531 

[16] https://nni.readthedocs.io/en/stable/sharings/kd_example.html 

[17] https://zhuanlan.zhihu.com/p/102038521

编辑：黄飞