神经网络的联想记忆功能可以分为两种,一是自联想记忆,另一种是异联想记忆。Hopfield神经网络就属于自联想记忆。由Kosko B.1988 年提出的双向联想记忆神经网络BAM(Bidirectional Associative Memory)属于异联想记忆。BAM有离散型﹑连续型和自适应型等多种形式。
8. CMAC模型
BP神经网络﹑Hopfield神经网络和BAM双向联想记忆神经网络分别属于前馈和反馈神经网络,这主要是从网络的结构来划分的。如果从神经网络的函数逼近功能这个角度来分,神经网络可以分为全局逼近网络和局部逼近网络。当神经网络的一个或多个可调参数(权值和阈值)在输入空间的每一点对任何一个输出都有影响,则称该神经网络为全局逼近网络,多层前馈BP网络是全局逼近网络的典型例子。对于每个输入输出数据对,网络的每一个连接权均需进行调整,从而导致全局逼近网络学习速度很慢,对于有实时性要求的应用来说常常是不可容忍的。如果对网络输入空间的某个局部区域只有少数几个连接权影响网络输出,则称网络为局部逼近网络。对于每个输入输出数据对,只有少量的连接权需要进行调整,从而使局部逼近网络具有学习速度快的优点,这一点对于有实时性要求的应用来说至关重要。目前常用的局部逼近神经网络有CMAC网络、径向基函数RBF网络和B样条网络等,其结构原理相似。
1975年J.S.Albus提出一种模拟小脑功能的神经网络模型,称为Cerebellar Model Articulation Controller,简称CMAC。CMAC网络是仿照小脑控制肢体运动的原理而建立的神经网络模型。小脑指挥运动时具有不假思索地作出条件反射迅速响应的特点,这种条件反射式响应是一种迅速联想。
CMAC 网络有三个特点:
(1)、作为一种具有联想功能的神经网络,它的联想具有局部推广(或称泛化)能力,因此相似的输入将产生相似的输出,远离的输入将产生独立的输出;
(2)、对于网络的每一个输出,只有很少的神经元所对应的权值对其有影响,哪些神经元对输出有影响则有输入决定;
(3)、CMAC的每个神经元的输入输出是一种线性关系,但其总体上可看做一种表达非线性映射的表格系统。由于CMAC网络的学习只在线性映射部分,因此可采用简单的δ算法,其收敛速度比BP算法快得多,且不存在局部极小问题。CMAC最初主要用来求解机械手的关节运动,其后进一步用于机械人控制、模式识别、信号处理以及自适应控制等领域。
9. RBF模型
对局部逼近神经网络,除CMAC神经网络外,常用的还有径向基函数RBF网络和B样条网络等。径向基函数(RBF,Radial Basis Function)神经网络,是由J.Moody 和C.Darken于20世纪80年代末提出的一种神经网络,径向基函数方法在某种程度上利用了多维空间中传统的严格插值法的研究成果。在神经网络的背景下,隐藏单元提供一个“函数”集,该函数集在输入模式向量扩展至隐层空间时为其构建了一个任意的“基”;这个函数集中的函数就被称为径向基函数。径向基函数首先是在实多变量插值问题的解中引入的。径向基函数是目前数值分析研究中的一个主要领域之一。
最基本的径向基函数(RBF)神经网络的构成包括三层,其中每一层都有着完全不同的作用。输入层由一些感知单元组成,它们将网络与外界环境连接起来;第二层是网络中仅有的一个隐层,它的作用是从输入空间到隐层空间之间进行非线性变换,在大多数情况下,隐层空间有较高的维数;输出层是线性的,它为作用于输入层的激活模式提供响应。
基本的径向基函数RBF网络是具有单稳层的三层前馈网络。由于它模拟了人脑中局部调整、相互覆盖接受域(或称感受域,Receptive Field)的神经网络结构,因此,RBF网络是一种局部逼近网络,现已证明它能以任意精度逼近任一连续函数.
RBF网络的常规学习算法,一般包括两个不同的阶段:
(1)、隐层径向基函数的中心的确定阶段。常见方法有随机选取固定中心法;中心的自组织选择法等。
(2)、径向基函数权值学习调整阶段。常见方法有中心的监督选择法;正则化严格插值法等。
10. SOM模型
芬兰Helsink大学Kohonen T.教授提出一种自组织特征映射网络SOM(Self-organizing feature Map),又称Kohonen网络。Kohonen认为,一个神经网络接受外界输入模式时,将会分为不同的对应区域,各区域对输入模式有不同的响应特征,而这个过程是自动完成的。SOM网络正是根据这一看法提出的,其特点与人脑的自组织特性相类似。
自组织神经网络结构
(1)、定义:自组织神经网络是无导师学习网络。它通过自动寻找样本中的内在规律和本质属性,自组织、自适应地改变网络参数与结构。
(2)、结构:层次型结构,具有竞争层。典型结构:输入层+竞争层。
输入层:接受外界信息,将输入模式向竞争层传递,起“观察”作用。
竞争层:负责对输入模式进行“分析比较,寻找规律,并归类。
自组织神经网络的原理
(1)、分类与输入模式的相似性:分类是在类别知识等导师信号的指导下,将待识别的输入模式分配到各自的模式类中,无导师指导的分类称为聚类,聚类的目的是将相似的模式样本划归一类,而将不相似的分离开来,实现模式样本的类内相似性和类间分离性。由于无导师学习的训练样本中不含期望输出,因此对于某一输入模式样本应属于哪一类并没有任何先验知识。对于一组输入模式,只能根据它们之间的相似程度来分为若干类,因此,相似性是输入模式的聚类依据。
(2)、相似性测量:神经网络的输入模式向量的相似性测量可用向量之间的距离来衡量。常用的方法有欧氏距离法和余弦法两种。
(3)、竞争学习原理:竞争学习规则的生理学基础是神经细胞的侧抑制现象:当一个神经细胞兴奋后,会对其周围的神经细胞产生抑制作用。最强的抑制作用是竞争获胜的“唯我独兴”,这种做法称为“胜者为王”,(Winner-Take-All)。竞争学习规则就是从神经细胞的侧抑制现象获得的。它的学习步骤为:A、向量归一化;B、寻找获胜神经元;C、网络输出与权调整;D、重新归一化处理。
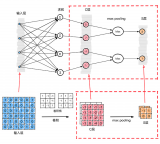
SOM网络的拓扑结构:SOM网络共有两层。即:输入层和输出层。
(1)、输入层:通过权向量将外界信息汇集到输出层各神经元。输入层的形式与BP网相同,节点数与样本维数相同。
(2)、输出层:输出层也是竞争层。其神经元的排列有多种形式。分为一维线阵,二维平面阵和三维栅格阵。最典型的结构是二维形式。它更具大脑皮层的形象。
输出层的每个神经元同它周围的其他神经元侧向连接,排列成棋盘状平面;输入层为单层神经元排列。
SOM权值调整域
SOM网采用的算法,称为Kohonen算法,它是在胜者为王WTA(Winner-Take-All)学习规则基础上加以改进的,主要区别是调整权向量与侧抑制的方式不同:WTA:侧抑制是“封杀”式的。只有获胜神经元可以调整其权值,其他神经元都无权调整。Kohonen算法:获胜神经元对其邻近神经元的影响是由近及远,由兴奋逐渐变为抑制。换句话说,不仅获胜神经元要调整权值,它周围神经元也要不同程度调整权向量。
SOM网络运行原理
SOM网络的运行分训练和工作两个阶段。在训练阶段,网络随机输入训练集中的样本,对某个特定的输入模式,输出层会有某个节点产生最大响应而获胜,而在训练开始阶段,输出层哪个位置的节点将对哪类输入模式产生最大响应是不确定的。当输入模式的类别改变时,二维平面的获胜节点也会改变。获胜节点周围的节点因側向相互兴奋作用也产生较大影响,于是获胜节点及其优胜邻域内的所有节点所连接的权向量均向输入方向作不同程度的调整,调整力度依邻域内各节点距离获胜节点的远近而逐渐减小。网络通过自组织方式,用大量训练样本调整网络权值,最后使输出层各节点成为对特定模式类敏感的神经元,对应的内星权向量成为各输入模式的中心向量。并且当两个模式类的特征接近时,代表这两类的节点在位置上也接近。从而在输出层形成能反应样本模式类分布情况的有序特征图。
11. CPN模型
1987年美国学者RobertHecht —Nielson提出了对偶传播神经网络(Counter--propagation Networks,简记为CPN)。CPN最早是用来实现样本选择匹配系统的。它能存储二进制或模拟值的模式对,因此CPN网络可以用作联想存储﹑模式分类﹑函数逼近和数据压缩等用途。与BP网相比,CPN的训练速度要快很多,所需的时间大约是BP网所需时间的1%。但是,它的应用面却因网络的性能相对来说比较窄。
从网络的拓扑结构来看,CPN与BP网类似,CPN是一个三层的神经网络,只不过这竞争层和输出层执行的训练算法是不同的。所以,称CPN 是一个异构网。与同构网相比,网络的异构性使它更接近于人脑。在人脑中存在有各种特殊的模块,它们使用完成不同的运算。例如,在听觉通道的每一层,其神经元与神经纤维在结构上的排列与频率的关系十分密切,对某一些频率,其中某些相应的神经元会获得最大的响应。这种听觉通道上的神经元的有序排列一直延续到听觉皮层。尽管许多低层次上的神经元是预先排列好的,但高层次上的神经元的组织则是通过学习自组织形成的。
在RobertHecht—Nielson提出的CPN神经网络中,其竞争层和输出层分别执行较早些时候出现的两个著名算法:即Kohonen l981年提出的自组织映射SOM算法和Grossberg l969年提出的外星(Outstar)算法。人们将执行自组织映射的层称为Kohonen层,执行外星算法的层则被称为Grossberg层。按这种方法将这两种算法组合在一起后所获得的网络,不仅提供了一种设计多级网训练算法的思路,解决了多级网络的训练问题,突破了单极网的限制,而且还使得网络具有了许多新的特点。多级网络的训练问题主要是在解决隐藏层神经元相应的联接权调整时,需要通过隐藏层神经元的理想输出来实现相关误差的估计。然而,它们对应的理想输出又是未知的。在无导师训练中是不需要知道理想输出的,因此可以考虑让网络的隐藏层执行无导师学习。这是解决多级网络训练的另一个思路。实际上,CPN就是将无导师训练算法与有导师训练算法结合在一起,用无导师训练解决网络隐藏层的理想输出未知的问题,用有导师训练解决输出层按系统的要求给出指定的输出结果的问题。
Kohonen提出的自组织映射由四部分组成,包括一个神经元阵列(用它构成CPN的Kohonen层),一种比较选择机制,一个局部互联,一个自适应过程。实际上,这一层将实现对输入进行分类的功能。所以,该层可以执行无导师的学习,以完成对样本集中所含的分类信息的提取。
Grossberg层主要用来实现类表示。由于相应的类应该是用户所要求的,所以,对应每—个输入向量,用户明确地知道它对应的理想输出向量,故该层将执行有导师的训练。两层的有机结合,就构成—个映射系统。所以,有人将CPN 看成一个有能力进行一定的推广的查找表(Look—up table)。它的训练过程就是将输入向量与相应的输出向量对应起来。这些向量可以是二值的,也可以是连续的。一旦网络完成了训练,对一个给定的输入就可以给出一个对应的输出。网络的推广能力表明,当网络遇到一个不太完整的、或者是不完全正确的输入时,只要该“噪音”是在有限的范围内,CPN 都可以产生一个正确的输出。这是因为Kohonen 层可以找到这个含有噪音的输入应该属于的分类,而对应的Grossberg层则可以给出该分类的表示。从整个网络来看,就表现出一种泛化能力。这使得网络在模式识别、模式完善、信号处理等方面可以有较好的应用。另外,上述映射的逆映射如果存在的话,可以通过对此网的简单扩展,来实现相应的逆变换。这被称为全对传网。
12. ART模型
在神经网络学习中,当网络规模给定后,由权矩阵所能记忆的模式类别信息量总是有限的,新输入的模式样本必然会对已经记忆的模式样本产生抵消或遗忘,从而使网络的分类能力受到影响。靠无限扩大网络规模解决上述问题是不现实的。如何保证在适当增加网络规模的同时,在过去记忆的模式和新输入的训练模式之间作出某种折中,既能最大限度地接收新的模式信息,同时又能保证较少地影响过去的样本模式呢? ART网络在一定程度上能较好解决此问题。
1976年,美国Boston大学CarpenterG.A.教授提出了自适应共振理论ART(Adaptive Resonance Theory)。随后Carpenter G.A.又与他的学生GrossbergS.合作提出了ART神经网络。
经过多年的研究和发展,ART 网络已有几种基本形式:
(1)、ART1型神经网络:处理双极性和二进制信号;
(2)、ART2型神经网络:它是ART1型的扩展,用于处理连续型模拟信号;
(3)、ART综合系统:将ART1和ART2综合在一起,系统具有识别﹑补充和撤消等综合功能。即所谓的3R(Recognition﹑Reinforcement﹑Recall)功能。
(4)、ART3型神经网络:它是一种分级搜索模型,兼容前两种结构的功能并将两层神经网络扩大为任意多层神经元网络,由于ART3型在神经元的模型中纳入了生物神经元的生物电-化学反应机制,因而它具备了很强的功能和扩展能力。
13. 量子神经网络
量子神经网络的概念出现于上个世纪90年代后期,一经提出后便引起了不同领域的科学家的关注,人们在这个崭新的领域进行了不同方向的探索,提出了很多想法和初步的模型,充分体现了量子神经网络研究的巨大潜力。主要研究方向可以概括为:
(1)、量子神经网络采用神经网络的连接思想来构造量子计算机,通过神经网络模型来研究量子计算中的问题;
(2)、量子神经网络在量子计算机或量子器件的基础上构造神经网络,充分利用量子计算超高速、超并行、指数级容量的特点,来改进神经网络的结构和性能;
(3)、量子神经网络作为一种混合的智能优化算法在传统的计算机上的实现,通过引入量子理论中的思想对传统神经网络改进,利用量子理论中的概念、方法(如态叠加、“多宇宙”观点等),建立新的网络模型;改善传统神经网络的结构和性能;
(4)、基于脑科学、认知科学的研究。
以上整理的内容主要摘自:
1. 《人工神经网络原理及应用》,2006,科学出版社
2. 《神经网络邮件分类算法研究》,2011,硕论,电子科技大学
3. 《人工神经网络原理、分类及应用》,2014,期刊,科技资讯
 电子发烧友App
电子发烧友App





















评论