基数估计算法就是使用准确性换取空间。 为了说明这一点,我们用三种不同的计算方法统计所有莎士比亚作品中不同单词的数量。请注意,我们的输入数据集增加了额外的数据以致比问题的参考基数更高。 这三种技术是:Java HashSet、Linear Probabilistic Counter以及一个Hyper LogLog Counter。结果如下:
该表显示,我们统计这些单词只用了512 bytes,而误差在3%以内。相比之下,HashMap的计数准确度最高,但需要近10MB的空间,你可以很容易地看到为什么基数估计是有用的。在实际应用中准确性并不是很重要的,这是事实,在大多数网络规模和网络计算的情况下,用概率计数器会节省巨大的空间。
再者,如果我们要实现记录网站每天访问的独立IP数量这样的一个功能:
集合实现:
使用集合来储存每个访客的 IP ,通过集合性质(集合中的每个元素都各不相同)来得到多个独立 IP,然后通过调用 SCARD 命令来得出独立 IP 的数量。
举个例子,程序可以使用以下代码来记录 2017 年 12 月 5 日,每个网站访客的 IP :
ip = get_vistor_ip() SADD'2017.12.5::unique::ip'ip
然后使用以下代码来获得当天的唯一 IP 数量:
SCARD'2017.12.5::unique::ip'
集合实现的问题
使用字符串来储存每个IPv4 地址最多需要耗费15 字节(格式为 ‘XXX.XXX.XXX.XXX’,比如’202.189.128.186’)。
下表给出了使用集合记录不同数量的独立 IP 时,需要耗费的内存数量:
独立IP数量 一天 一个月 一年
一百万 15 MB 450 MB 5.4 GB
一千万 150 MB 4.5 GB 54 GB
一亿 1.5 GB 45 GB 540 GB
随着集合记录的 IP 越来越多,消耗的内存也会越来越多。另外如果要储存 IPv6 地址的话,需要的内存还会更多一些。为了更好地解决像独立 IP 地址计算这种问题,Redis 在 2.8.9 版本添加了 HyperLogLog 结构。
Redis数据结构HyperLogLog
Redis HyperLogLog 是用来做基数统计的算法,HyperLogLog 的优点是,在输入元素的数量或者体积非常非常大时,计算基数所需的空间总是固定的、并且是很小的。在Redis 里面,每个 HyperLogLog 键只需要花费 12 KB 内存,就可以计算接近 2^64 个不同元素的基数。这和使用集合计算基数时,元素越多耗费内存就越多的集合形成鲜明对比。但是,因为 HyperLogLog 只会根据输入元素来计算基数,而不会储存输入元素本身,所以 HyperLogLog 不能像集合那样,返回输入的各个元素。
什么是基数?
比如数据集 {1, 3, 5, 7, 5, 7, 8}, 那么这个数据集的基数集为 {1, 3, 5 ,7, 8}, 基数(不重复元素)为5。 基数估计就是在误差可接受的范围内,快速计算基数。
估算值:算法给出的基数并不是精确的,可能会比实际稍微多一些或者稍微少一些,但会控制在合理的范围之内。
几个命令
将元素添加至 HyperLogLog
1、PFADD key element [element …]
将任意数量的元素添加到指定的 HyperLogLog 里面。
这个命令可能会对 HyperLogLog 进行修,以便反映新的基数估算值,如果 HyperLogLog 的基数估算值在命令执行之后出现了变化,那么命令返回1,否则返回0。
命令的复杂度为 O(N) ,N 为被添加元素的数量。
2、PFCOUNT key [key …]
返回给定 HyperLogLog 的基数估算值。
当只给定一个 HyperLogLog 时,命令返回给定 HyperLogLog 的基数估算值。
当给定多个 HyperLogLog 时,命令会先对给定的 HyperLogLog 进行并集计算,得出一个合并后的HyperLogLog ,然后返回这个合并 HyperLogLog 的基数估算值作为命令的结果(合并得出的HyperLogLog 不会被储存,使用之后就会被删掉)。
当命令作用于单个 HyperLogLog 时, 复杂度为 O(1) , 并且具有非常低的平均常数时间。
当命令作用于多个 HyperLogLog 时, 复杂度为 O(N) ,并且常数时间也比处理单个 HyperLogLog 时要大得多。
PFADD 和 PFCOUNT 的使用示例
redis>PFADD unique::ip::counter'192.168.0.1'(integer)1redis>PFADD unique::ip::counter'127.0.0.1'(integer)1redis>PFADD unique::ip::counter'255.255.255.255'(integer)1redis>PFCOUNT unique::ip::counter(integer)3
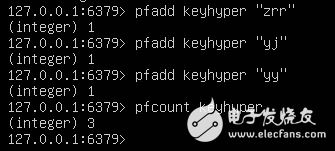
合并多个 HyperLogLog
3、PFMERGE destkey sourcekey [sourcekey …]
将多个 HyperLogLog 合并为一个 HyperLogLog ,合并后的 HyperLogLog 的基数估算值是通过对所有给定 HyperLogLog 进行并集计算得出的。
PFMERGE 的使用示例
redis> PFADD str1"apple""banana""cherry"(integer)1redis> PFCOUNT str1 (integer)3redis> PFADD str2"apple""cherry""durian""mongo"(integer)1redis> PFCOUNT str2 (integer)4redis> PFMERGE str1&2str1 str2 OK redis> PFCOUNT str1&2(integer)5Hyperloglog算法浅说
这个算法的目的:比如给你一个数组,int a[]={1,1,2,6,9,8,5,4,1,2},则这个数组里一共有十个元素,其中distinct的数一共有7个,它们是1,2,4,5,6,8,9。
这个算法就是判断输入流中互不相同的元素一共有多少个。这个算法是概率算法,但是它的精确度很高。
该算法出自论文《HyperLogLog the analysis of a near-optimal cardinality estimation algorithm》,下载链接:。具体论文的理论推导不详细介绍,简述下其思想核心。
在理想状态下,将一堆数据hash至[0,1],每两点距离相等,1/间距即可得出这堆数据的基数。然而实际情况往往不能如愿,只能通过一些修正不断的逼近这个实际的基数。实际采用的方式一是分桶,二是取kmax。分桶将数据分为m组,每组取第k个位置的值,所有组中得到最大的kmax,(k-1)/kmax得到估计的基数。
HLL算法的另一个主观上的理解可以用抛硬币的方式来理解。以当硬币抛出反面为一次过程,当你抛n次硬币全为正面的概率为1/2^n。当你经历过k(k很大时)次这样的过程,硬币不出现反面的概率基本为0。假设反面为1,正面为0,每抛一次记录1或者0,当记录上显示为0000000…001时,这种可以归结为小概率事件,基本不会发生。转换到基数的想法就是,可以通过第一个1出现前0的个数n来统计基数,基数大致为2^(n+1)时。硬币当中可以统计为(1/2*1+1/4*2+1/8*3…),大致可以这么去想。
我们首先需要以下几个辅助函数或者数据
1、int hash(type input);//将输入的元素hash成一个32bit的整数,输入可能是整数,也可能是字符串,甚至是结构体,etc
2、unsigned int position(int input);//返回input的二进制表示中,从左往右数,第一个1出现的位置,比如
position(1000000100000111110)=1position(0001111000011100000)=4position(000000)=7
3、m=2^b,其中b在[4,16]之间
4、几个常数
constdoublea16=0.673constdoublea32=0.697constdoublea64=0.709constdoubleam=0.7213/(1+1.079/m) (m>=128)
有了这四个准备之后,我们就可以开始用hyperloglog来实现计数了:m=2^b个计数器,M[1]到M[m]都初始化为0
for(v=input) {x=hash(v); j=1+
 电子发烧友App
电子发烧友App























评论