方向梯度直方图(Histogram of Oriented Gradient, HOG)
特征是一种在计算机视觉和图像处理中用来进行物体检测的特征描述子。HOG特征通过计算和统计图像局部区域的梯度方向直方图来构成特征。
在一副图像中,局部目标的表象和形状能够被梯度或边缘的方向密度分布很好地描述。其本质为:梯度的统计信息,而梯度主要存在于边缘的地方
Hog特征结合SVM分类器已经被广泛应用于图像识别中,尤其在行人检测中获得了极大的成功。
实现方法:
2、首先将图像分成小的连通区域,这些连通区域被叫做细胞单元。然后采集细胞单元中各像素点的梯度的或边缘的方向直方图。最后把这些直方图组合起来,就可以构成特征描述符。
3、性能提高:
将这些局部直方图在图像的更大的范围内(叫做区间)进行对比度归一化,可以提高该算法的性能,所采用的方法是:先计算各直方图在这个区间中的密度,然后根据这个密度对区间中的各个细胞单元做归一化。通过这个归一化后,能对光照变化和阴影获得更好的效果。
因此HOG特征是特别适合于做图像中的人体检测的 。
1、色彩和伽马归一化。
A)、什么是图像的归一化
图像归一化是指对图像进行了一系列标准的处理变换,使之变换为一固定标准形式的过程,该标准图像称作归一化图像。
这样可以减少光照因素的影响
2、计算图像梯度
计算图像横坐标和纵坐标方向的梯度,计算每个像素位置的梯度方向值;
从原始图像当中抽象出来的数据图像数字符号等等的这些标记称为图像特征。
唯一性,完整性,几何变换不变性,名感性,抽象性
运用图像分割的方法,进行处理成为
1) 面积
2) 位置为图像执行的位置,图像的之心的计算法方法是
位置为质心所在的位置
为转动惯量最小的那个轴,使得所有的点距离该轴的距离的欧氏距离最小。
使用链码表示物体的边界
链码就是用来表示目标物体边界上的点的数值序列,可以结婚时呢个存储信息,而且可以准确的去顶物体的一些信息。
链码就是用来表示目标物体边界上的点的数值序列,可以结婚时呢个存储信息,而且可以准确的去顶物体的一些信息。
什么是链码表
原链码:
归一化链码:
原链码具有平移不变性,但是当起点不同时候,会有不同的链码,所以要使用归一化链码,确定那个起始点,使得链码的存储数据最小。
差分码:
由于归一化链码不具有旋转不变性,于是定义了差分链码。
傅里叶描述子(傅里叶变换的一个作用就是使得在信息量不发生变化的情况下将数据的表达形式发生变化,例如卷积,就是将数据从以为变化到二维空间当中)。
采用傅里叶描述的一个优点是讲二维问题转化为一维问题,
使用傅里叶描述子的方法是:省略后面的n-m个点。
除此之外还有偏心度。
什么叫做矩:
矩在统计学中可以表征随机变量的分布,而在力学中用于表征特征物质的分布。
二值图是一种二维密度的分布函数。
二维矩不变理论p+q阶矩的定义:
P+q阶矩的定义
其中,x拔和y拔是图像的灰度的中心点。
直方图特征
数字图像可以看作是一个二维随机过程的一个样本,用联合该类分布来描述。
例如:图像灰度直方图可以描述图像的灰度分布情况,(图像的灰度直方图就是使用概率分布来表述这些特征在图像中的分布的情况。)
B表示了灰度级别,该灰度b在图像中出现的频率P(b)m表示了图像中的总像素数目。N(b)表示像素为灰度值b的数目。
P(b)表示了区域的概率密度函数。
直方图给出了灰度图像额全局描述。在实际当中使用从直方图中提取出来的一阶统计测度。来区别类别间的特征差异
有均值,方差,能量,熵、偏度
偏度:
数据集关于中心点u分布的对称情况。
如果大于零,则表示图像像素偏于中心点的右边。
在图像处理领域当中,均值u反应图像的平均亮度,方差反应图像灰度级分布的分散性。但是这两个值容易受到图像采样情况的影响。 所以应该对他图像进行归一化处理。。使得所有图像中的所有图像都具有相同的均值和方差。 能量是灰度分布对于原点的二阶矩,如果图像灰度值的等概率分布,则能量最小,熵是图像中信息量多少的反应,对于等概率分布,熵最大。
2、特征直方图
设 N(xi)为图像II中某一特征值为xi的像素个数.M为像素总数。
图象的特征直方图为
特征直方图就是某一个特征的该类分布,例如,对于灰度图像,直方图就是灰度的概率分布。
3、什么是梯度方向直方图
即将梯度的方向正在(-Pi/2,pi/2)中分成k个均匀的区域,
或者是梯度幅值的其他形式。但是他们都可以在一定的程度上反应像素上一定的边缘信息。
每一个像素点附近的梯度特征是一个k维向量。
图像的梯度方向直方图就是图像中所有像素点的k维团体都特征进行的直方图统计。
3.1、梯度主要存在与边缘的地方重点内容**
使用hog特征对物体来进行特征描述。
1、 图像的归一化,传统的图像归一化一般采用gamma标准化形式:
b) 根据梯度计算的公式讲每个像素的梯度赋值和方向。
c) 直方图统计的放个单元划分。将图像分成单元和块。一个图像由若干个放个单元组成,
d) 计算一个块当中的hog特征向量。计算一个放个单元的k个梯度特征,对于由n*n个相邻方格组成的块,将每个方格单元的梯度特征组合在一起,就可以得到这个块的特征向量。该特征向量是n*n*k维度。
e) 对hog特征向量进行归一化,归一化操作是对块进行的,主要是为了使得特征向量空间对光照阴影和变化具有鲁棒性。归一化常用的函数如下:
6)特征向量的生成
在图像上以一个放个单元为步长对块进行华东,将每个块的特征组hi在一起,就可以得到图像的hog特征。
这样得到的hog特征向量是
3.2 hog特征提取的快速算法
上面给出的是穷举搜索算法,计算量偏大,基于积分直方图的hog的特征提取方法。
使用H(x,y,k) = H(x-1,y,k)+ H(x,y-1,k)+ H(x-1,y-1,k)+Q(x,y)。这个迭代的式子来计算(x,y)点出的积分直方图。
其中q(x,y)为在点(x,y)处的梯度向量计算公式。
计算处各个点处的对应的直方图之后,图8-13中区域v的直方图Hv计算公式为:
这样计算出来的梯度方向直方图,可以节省大量的计算时间。
第二篇:csdn上的学习资料重点内容
Hog方向梯度直方图和svm支持向量机的结合是图像识别中的广泛使用的一种方法。
HOG+SVM进行行人检测的方法是法国研究人员Dalal在2005的CVPR上提出的。
先将图像划分为许多小的联通区域(细胞单元),然后采集细胞单元中各个像素点的梯度或者边缘的方向直方图。最后将这些直方图组合起来就可以构成特征描述器。
此处的计算梯度方向的方法的原理是使用偏微分,实际上使用的是使用微分的定义式来进行的。这里使用的是一个以为的离散微分模板,将图像同时在水平方向和垂直方向进行处理。
注意:微分的计算公式是dy/dx,在这里没有除以dx,是因为dx就等于1.
把各个细胞单元组合成大的、空间上连通的区间(blocks)。这样,一个block内所有cell的特征向量串联起来便得到该block的HOG特征。这些区间是互有重叠的,这就意味着:每一个单元格的特征会以不同的结果多次出现在最后的特征向量中。我们将归一化之后的块描述符(向量)就称之为HOG描述符。
行人检测的最佳参数设置是:3×3细胞/区间、6×6像素/细胞、9个直方图通道。则一块的特征数为:3*3*9;
Hog的核心的思想是物体的边缘你的梯度直方图能够被边缘方向的直方图和光强强度梯度描述。所以就使用边缘方向来描述物体的边界,进而为区分物体做好基础。而直方图能够表述整个图像的各种特征信息在图像上的分布情况。
此步就是为图像的每个细胞单元构建梯度方向直方图。细胞单元中的每一个像素点都为某个基于方向的直方图通道投票。
投票是采取加权投票(weighted voting)的方式,即每一票都是带权值的,这个权值是根据该像素点的梯度幅度计算出来。
可以采用幅值本身或者它的函数来表示这个权值,实际测试表明: 使用幅值来表示权值能获得最佳的效果,当然,也可以选择幅值的函数来表示,比如幅值的平方根、幅值的平方、幅值的截断形式等。
细胞单元可以是矩形的,也可以是星形的。直方图通道是平均分布在无向(0~180度)或有向(0~360度)范围内。
作者发现,采用无向的梯度和9个直方图通道,能在行人检测试验中取得最佳的效果。
把细胞单元组合成大的区间。
由于局部光照的变化以及前景-背景对比度的变化,使得梯度强度的变化范围非常大。这就需要对梯度强度做归一化。
梯度强度归一化采取的办法是:把各个细胞单元组合成大的、空间上连通的区间(blocks)。 这样以来,HOG描述器就变成了由各区间所有细胞单元的直方图成分所组成的一个向量(就是说,hog描述器就是一个向量,向量中每一个元素就是每一个细胞单元的直方图而每一个细胞单元的直方图就是在k个方向上梯度的投影所组成的向量)。
这些区间是互有重叠的,这就意味着:每一个细胞单元的输出都多次作用于最终的描述器。区间有两个主要的几何形状:矩形区间(R-HOG)和环形区间(C-HOG)。
R-HOG区间大体上是一些方形的格子,它可以有三个参数来表征:每个区间中细胞单元的数目、每个细胞单元中像素点的数目、每个细胞的直方图通道数目。作者通过实验表明,行人检测的最佳参数设置是:3×3细胞 /区间、6×6像素/细胞、9个直方图通道。
作者还发现,在对直方图做处理之前,给每个block加一个高斯空域窗口(Gaussian spatial window)是非常必要的,因为这样可以降低边缘的周围像素点的权重。R- HOG跟SIFT描述器看起来很相似,但他们的不同之处是:R-HOG是在单一尺度下、密集的网格内、没有对方向排序的情况下被计算出来;而SIFT描述器是在多尺度下、稀疏的图像关键点上、对方向排序的情况下被计算出来。补充一点,R-HOG是各区间被组合起来用于对空域信息进行编码,而SIFT的各描述器是单独使用的。
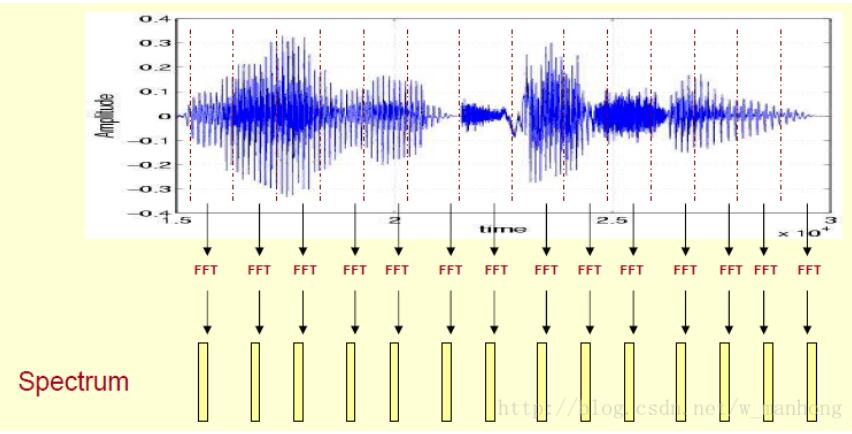
照这个直方图来看的话,就是
对梯度进行归一化处理: 区间归一化(Block normalization Schemes) 引入v表示一个还没有被归一化的向量它包含了给定区间(block)的所有直方图信息。| | vk | |表示v的k阶范数,这里的k去1、2。用e表示一个很小的常数。这时,归一化因子可以表示如下:
 电子发烧友App
电子发烧友App










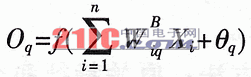

















评论