从零开始在FPGA上实现IIR滤波器

描述

滤波可能是任何嵌入式工程师必须设计的最常见的 DSP 算法，无论他们是为 STM32、TI DSP 还是为 FPGA 开发的算法。滤波非常重要，因为大多数应用程序都连接到现实世界，因此它们需要捕获具有所有真实信号都具有的不良元素的真实信号，即噪声、偏移……此外，我们需要获取的信号，并非总是如此将是我们获取的主要信号，例如，对于生物信号，我们将获取与电网频率相对应的 50 或 60 Hz 的高电平。在这种情况下，我们将需要一个过滤器。

作为本博客的读者，您肯定知道，在数字系统上，我们有 2 种滤波器，FIR（有限脉冲响应）滤波器，它只使用现在输入的值和过去的值，以及 IIR（无限脉冲Response），它使用现在和过去的输入值，以及过去输出的值。FIR 滤波器很容易为许多应用设计，但它们的响应对于低阶滤波器是有限的。另一方面，使用 IIR 滤波器，我们可以实现更积极的响应，但它们的缺点是滤波器在某些情况下可能不稳定。在本文中，我们将了解如何逐步实现二阶滤波器，从滤波器设计到 Verilog 实现。

设计 IIR 滤波器的过程始终相同。首先我们要使用它的连续传递函数来设计滤波器，然后，一旦选择了滤波器的固有频率、阶数和品质因数，我们将得到相应的 s

功能。为了将该滤波器数字化，下一步是应用一些变换来用 z 替换变量s ，这个过程称为离散化。为了离散化连续传递函数，我们可以使用多种方法，其中一种易于使用的方法是Tustin或双线性变换。

双线性变换基于将连续传递函数中的s变量替换为z的函数。在下一个示例中，我们可以看到应用双线性变换对单极点低通滤波器进行离散化。接下来是我们必须在连续传递函数中执行的替换。

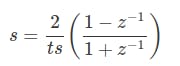
对于单极点滤波器，这些将是执行双线性变换的步骤。低通单极滤波器的方程如下：

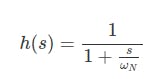
应用转换，我们有：

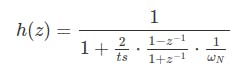
与分母运算以获得共同的分母，

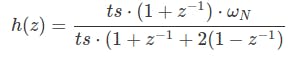
然后，我们需要将元素与其他元素中的z分开，最后我们将得到一个z函数，该函数取决于滤波器的采样频率和固有频率。

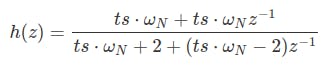
在 MATLAB 中，我们可以使用以下命令进行此转换hz = c2d(hs,ts,'Tustin')

接下来是 100 Hz 低通滤波器的整个 MATLAB 代码。

%% single pole filter discretization

% continuos filter declaration
s = tf('s');

% define characteristics of the filter
fc = 100; 

% compute angular frequency
wc = 2*pi*fc;

% Write the transfer function of a low pass single pole filter
hs = 1/(1+s/wc);

% show its bode diagram
bode(hs)

% discretization using tustin method

% Sampling frequency
fs = 100e3;

ts = 1/fs;

hz = c2d(hs,ts,'Tustin')

赫兹的结果是

hz =
 
  0.003132 z + 0.003132
  ---------------------
       z - 0.9937
 
Sample time: 1e-05 seconds
Discrete-time transfer function.

为了验证我们手动获得的方程是否正确，我们必须使用我们之前获得的值创建一个传递函数。

hz_man = tf([ts*wc, ts*wc],[ts*wc+2 ts*wc-2], ts)

这种情况下的结果是

hz_man =
 
  0.006283 z + 0.006283
  ---------------------
     2.006 z - 1.994
 
Sample time: 1e-05 seconds
Discrete-time transfer function.

我们可以看到，将分子和分母除以 2.006，方程与使用c2c命令得到的方程相同。

双线性变换与其他任何离散化方法一样，都是一种近似，因此我们将引入一些误差。该误差的大小与采样频率有关，因为在某些情况下，非常（非常）高的采样频率可能看起来是连续的。在实际系统中，采样频率取决于 ADC 和许多实际组件，我们可以使用高采样频率，但在其他情况下，我们会引入显着误差。

在双线性变换的情况下，我们将引入的误差之一是频率扭曲。这种效应会产生滤波器固有频率的偏移。这种影响在低通滤波器的情况下可以忽略不计，但在窄带滤波器的情况下，该误差可能使滤波器不起作用。

为了找到由双线性变换引起的误差，我们需要找到模拟频率与离散频率之间的关系。首先，我们将从双线性变换方程开始。

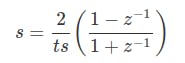
将z替换为其极坐标形式e^(jωd) ，我们有

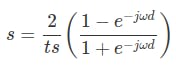
现在，我们将使用半角分割指数。

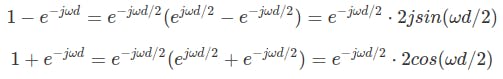
将分子和分母替换为上述等式，我们有：

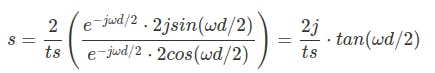
现在，我们将使用半角分割指数。

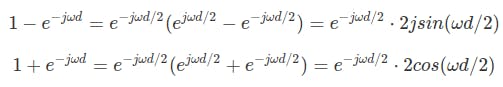
将分子和分母替换为上述等式，我们有：

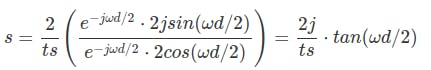
然后，我们必须找到与类比的关系，所以我们要使两个方程相等

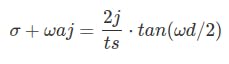
我们可以验证实部为 0，而虚部wwa直接为

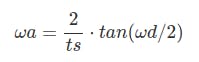
请注意，当ts趋于零时，极限是ωa = ωd。

在 MATLAB 中，我们可以很容易地检查这个偏差。在这种情况下，我们将声明一个二阶连续带阻滤波器。然后使用 Tustin 方法对滤波器进行离散化。

close all
clear all
clc

% define filter
fc = 3000;
wn = 2*pi*fc;
q = 5;%1/sqrt(2); % butterworth

s = tf('s');

h = (s^2+wn^2)/(s^2+wn/q*s+wn^2)

%bode(h)

% discretize filter
fs = 100e6/2048 % prescale FPGA frequency by factor of 2048
ts = 1/fs;

hz = c2d(h,ts,'tustin');

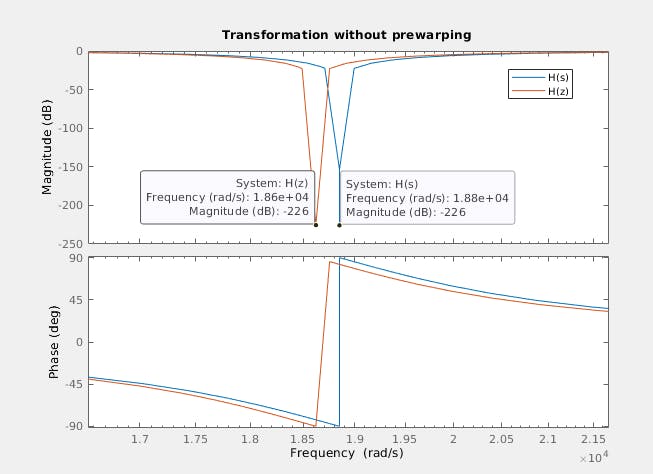
我们可以看到数字滤波器的频率是如何移动的。然后我们将对自然频率应用预变形，并使用这个新频率重新离散化滤波器。

% calculate prewarping
wp = 2/ts*tan(wc*ts/2);
hw = (s^2+wp^2)/(s^2+wp/q*s+wp^2)
hwz = c2d(hw,ts,'tustin');

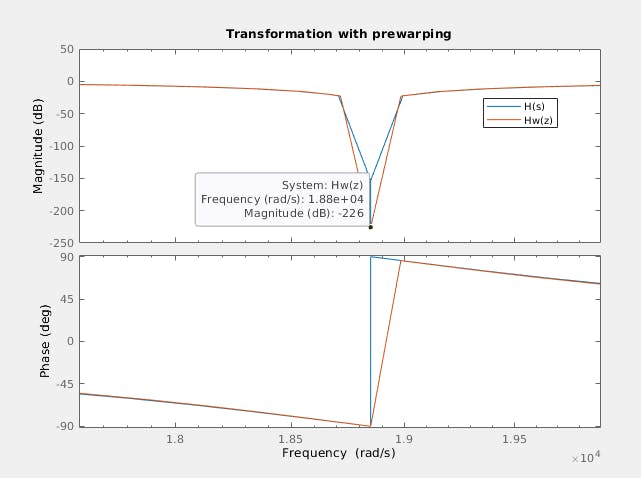
我们可以看到在这种情况下，两个频率是相同的，所以误差是固定的。

为了在现实世界中验证这种行为，我们将在 Verilog 中实现这个二阶带阻滤波器，然后我们将检查扭曲错误，然后如何使用预扭曲来修复它。

在开始编码之前，我们必须考虑我们想要创建的模块是什么。在我的情况下，能够参数化模块是非常重要的，这样，如果我改变输入的宽度，或者输出的宽度，那只代表一个参数的改变，而不需要修改模块的代码因为这意味着模块的新测试。此外，我们必须考虑我们将使用什么数字格式。对于这种过滤器，很明显我们需要有符号格式，以及管理十进制数的能力. 为了达到这个要求，我们必须在定点和浮点之间进行选择，对我来说决定很明确，我想要一个可以单独实例化的代码，没有外部浮点单元，所以格式将是定点的。如果我们加上参数的要求，和定点格式，我们需要参数来定义信号的宽度，还有小数部分的宽度，这与我们需要的精度有关。此外，将选择精度以获得与设计尽可能相似的实施滤波器的响应。现在，我们需要参数化多少宽度？我们可以定义一个宽度，用于输入和输出以及系数，但是这样，系数的宽度将根据数据生成器的宽度来选择，对于某些过滤器，系数在稳定极限上，这可能代表一个问题。因此，至少我们将定义 2 种不同的宽度，一种用于输入和输出，根据数据消耗和数据源，另一种根据我们需要的分辨率。另一个我们要考虑宽度的事情，是内部运算的分辨率，因为在某些情况下，稳定性问题与系数本身的宽度无关，而是运算分辨率，所以在这一点上，将是有趣的解耦将在 MATLAB 或 Python 上生成的系数的宽度，以及内部滤波器操作的宽度。最后，过滤器参数将如下所示。一个用于输入和输出，根据数据消耗和数据源，另一个根据我们需要的分辨率。另一个我们要考虑宽度的事情，是内部运算的分辨率，因为在某些情况下，稳定性问题与系数本身的宽度无关，而是运算分辨率，所以在这一点上，将是有趣的解耦将在 MATLAB 或 Python 上生成的系数的宽度，以及内部滤波器操作的宽度。最后，过滤器参数将如下所示。一个用于输入和输出，根据数据消耗和数据源，另一个根据我们需要的分辨率。另一个我们要考虑宽度的事情，是内部运算的分辨率，因为在某些情况下，稳定性问题与系数本身的宽度无关，而是运算分辨率，所以在这一点上，将是有趣的解耦将在 MATLAB 或 Python 上生成的系数的宽度，以及内部滤波器操作的宽度。最后，过滤器参数将如下所示。稳定性问题与系数本身的宽度无关，而与运算分辨率有关，因此在这一点上，将在 MATLAB 或 Python 上生成的系数的宽度与内部滤波器操作的宽度解耦会很有趣. 最后，过滤器参数将如下所示。稳定性问题与系数本身的宽度无关，而与运算分辨率有关，因此在这一点上，将在 MATLAB 或 Python 上生成的系数的宽度与内部滤波器操作的宽度解耦会很有趣. 最后，过滤器参数将如下所示。

parameter inout_width = 16,
parameter inout_decimal_width = 15,
parameter coefficient_width = 16,
parameter coefficient_decimal_width = 15,
parameter internal_width = 16,
parameter internal_decimal_width = 15

接下来我们必须考虑接口。在模块之间以连续方式传输数据的应用中，AXI4-Stream 将是最佳选择。在输入和输出字段中，我们将定义主从 AXI4-Stream 接口来获取和发送数据。尽管输入和输出宽度是参数化的，但如果我们想将模块连接到现有的 AXI4-Stream IP，则此宽度受限于总线的宽度。

input aclk,
input resetn,

/* slave axis interface */
input [inout_width-1:0] s_axis_tdata,
input s_axis_tlast,
input s_axis_tvalid,
output s_axis_tready,

/* master axis interface */
output reg [inout_width-1:0] m_axis_tdata,
output reg m_axis_tlast,
output reg m_axis_tvalid,
input m_axis_tready,

关于系数，插入它们最好是使用 AXI4-Lite 接口，但我想设计这个模块而不需要使用 Zynq 或 Microblaze，所以插入系数的简单方法是作为输入。

/* coefficients */
input signed [pw_coefficient_width-1:0] b0,
input signed [pw_coefficient_width-1:0] b1,
input signed [pw_coefficient_width-1:0] b2,
input signed [pw_coefficient_width-1:0] a1,
input signed [pw_coefficient_width-1:0] a2

现在，在定义了所有输入和输出之后，我们必须考虑数据流。首先，由于我们定义了不同的格式，为了能够在系数和数据之间进行运算，我们必须将所有信号的格式更改为内部格式，内部格式由内部宽度和小数宽度定义。使用的整数宽度被定义为一个localparam，并且对应于宽度和小数宽度之间的差异。要更改格式，我们将在信号的低端填充零，直到完成小数部分。对于整数部分，由于使用的格式是有符号的，我们必须进行符号扩展，即填充 MSb 的值，直到整数部分完成。请注意，这是有效的，因为内部宽度大于或等于输入输出和系数宽度。

/* resize signals to internal width */
assign input_int = { {(internal_integer_width-inout_integer_width){s_axis_tdata[inout_width-1]}},
                          s_axis_tdata,
                          {(internal_decimal_width-inout_decimal_width){1'b0}} };
assign b0_int = { {(internal_integer_width-coefficient_integer_width){b0[coefficient_width-1]}},
                          b0,
                          {(internal_decimal_width-coefficient_decimal_width){1'b0}} };
assign b1_int = { {(internal_integer_width-coefficient_integer_width){b1[coefficient_width-1]}},
                          b1,
                          {(internal_decimal_width-coefficient_decimal_width){1'b0}} };
assign b2_int = { {(internal_integer_width-coefficient_integer_width){b2[coefficient_width-1]}},
                          b2,
                          {(internal_decimal_width-coefficient_decimal_width){1'b0}} };
assign a1_int = { {(internal_integer_width-coefficient_integer_width){a1[coefficient_width-1]}},
                          a1,
                          {(internal_decimal_width-coefficient_decimal_width){1'b0}} };
assign a2_int = { {(internal_integer_width-coefficient_integer_width){a2[coefficient_width-1]}},
                          a2,
                          {(internal_decimal_width-coefficient_decimal_width){1'b0}} };

数字滤波器，无论是 FIR 还是 IIR，都需要存储过去输入的值，而 IIR 还需要存储过去输出的值，因此我们需要一个流水线结构来存储过去的值。

/* pipeline registers */
always @(posedge aclk)
  if (!resetn) begin
    input_pipe1 <= 0;
    input_pipe2 <= 0;
    output_pipe1 <= 0;
    output_pipe2 <= 0;
  end
  else
    if (s_axis_tvalid) begin
      input_pipe1 <= input_int;
      input_pipe2 <= input_pipe1;
      output_pipe1 <= output_int;
      output_pipe2 <= output_pipe1;
    end

现在，接下来是执行过滤器计算。一个二阶滤波器需要执行 5 次乘法，记住这并不意味着模块使用 5 个 DSP slice。我开发的代码执行组合乘法。这允许 0 个时钟周期延迟，但会限制滤波器的速度。如果您的时序约束没有得到满足，您可以注册乘法器的输入，然后进行重新定时，让 Vivado 选择更有效的放置寄存器的位置。

/* combinational multiplications */
assign input_b0 = input_int * b0_int;
assign input_b1 = input_pipe1 * b1_int;
assign input_b2 = input_pipe2 * b2_int;
assign output_a1 = output_pipe1 * a1_int;
assign output_a2 = output_pipe2 * a2_int;

乘法的结果将在输入的情况下相加，在输出的情况下相减，以获得滤波器输出。由于乘积的输出大小是操作数的两倍，因此加法必须是相同的宽度。要在乘法上使用输出，我们必须执行移位以删除额外的小数位。关于额外的整数位置将在分配时被截断。

assign output_2int = input_b0 + input_b1 + input_b2 - output_a1 - output_a2;
assign output_int = output_2int >>> (internal_decimal_width);

最后，输出的值将被重新格式化为输入输出宽度。

assign m_axis_tdata = output_int >>> (internal_decimal_width-inout_decimal_width);

对于 AXI4-Stream 管理信号，由于滤波器作为桥接器，有 1 个周期延迟，因此管理信号会以 1 个周期延迟通过滤波器。

至此，我们已经实现了 Verilog 模块并准备好用作带阻滤波器。接下来是使用该tfdata函数在 MATLAB 中获取系数。关于过滤器的宽度，我们将使用 18 位分辨率用于小数部分，2 用于整数部分，以使过滤器达到 +-2。接下来是获取定点系数的 MATLAB 代码。

% filter implemetation

[num, den] = tfdata(hwz)

b0 = num{1}(1)
b1 = num{1}(2)
b2 = num{1}(3)
a1 = den{1}(2)
a2 = den{1}(3)

% quantize

fracBits = 18;

b0_qq = floor(b0*2^fracBits)
b1_qq = floor(b1*2^fracBits)
b2_qq = floor(b2*2^fracBits)

a1_qq = floor(a1*2^fracBits)
a2_qq = floor(a2*2^fracBits)

这将返回下一个结果。

b0_qq =

      252631


b1_qq =

     -468081


b2_qq =

      252631


a1_qq =

     -468081


a2_qq =

      243119

一旦我们有了五个系数，我们必须将它们作为输入引入 Verilog 模块中的系数输入。

axis_biquad_v1_0 #(
  .inout_width(15),
  .inout_decimal_width(13),
  .coefficient_width(20),
  .coefficient_decimal_width(18),
  .internal_width(20),
  .internal_decimal_width(18)
  ) axis_biquad_inst0 (
  .aclk(clk100mhz),
  .resetn(pll_locked),
  /* slave axis interface */
  .s_axis_tdata({axis_data_signal_ch1[13], axis_data_signal_ch1}),
  .s_axis_tlast(),
  .s_axis_tvalid(&filter_prescaler),
  .s_axis_tready(),
  /* master axis interface */
  .m_axis_tdata(axis_data_signal_filt),
  .m_axis_tlast(),
  .m_axis_tvalid(),
  .m_axis_tready(),
  /* coefficients */
  .b0(20'd252631),
  .b1(-20'd468081),
  .b2(20'd252631),
  .a1(-20'd468081),
  .a2(20'd243119)
  );

为了验证这种效果是否发生，并使用预变形修复，我将使用带有 ZMOD Scope 和 ZMOD AWG的Digilent 的 Eclypse Z7 。此外，为了生成信号并验证滤波器的响应，我将使用全新的 Analog Discovery PRO 5250 ，它具有信号 125 Msps 信号发生器以及能够获取高达 1 Gsps 的两通道示波器。

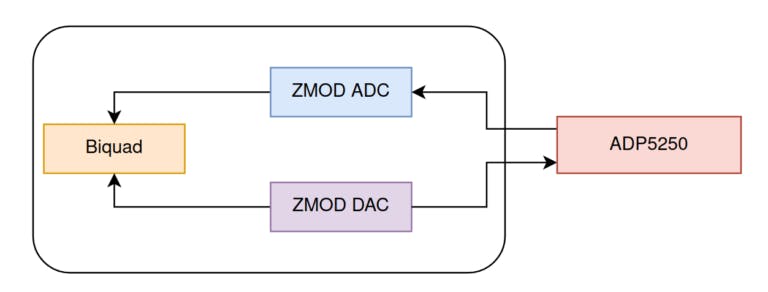
为了获得自然离散频率 ( ωd )，我将使用 ADP 5250 的一个非常有用的功能，它执行频率扫描，为每个频率获取滤波器的增益，因此结果将是滤波器的波特图. 要配置此模式，我们需要打开工具网络。

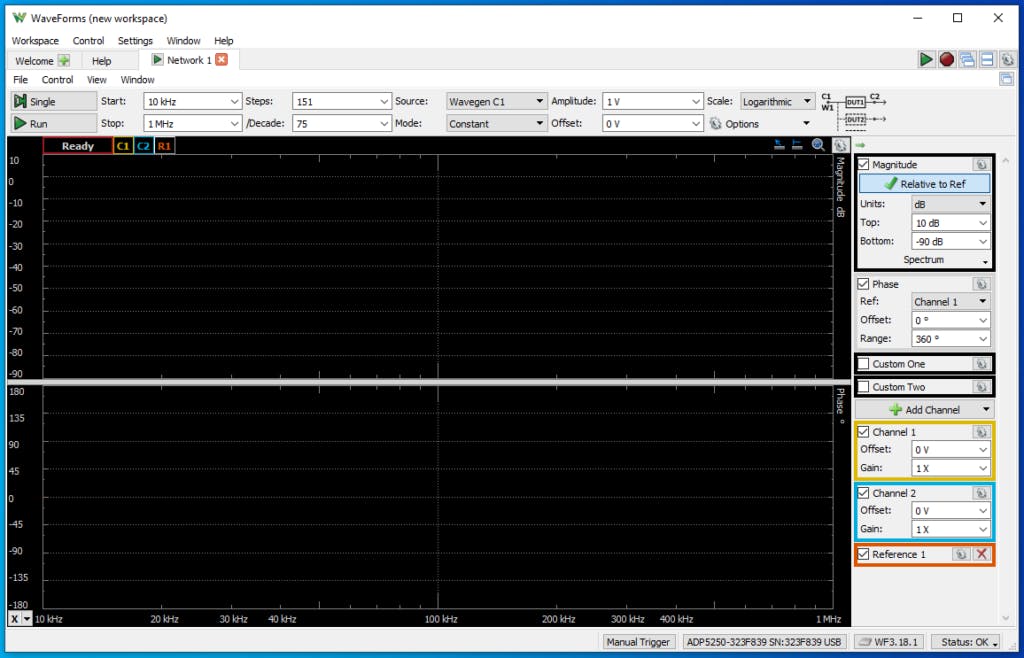
打开此工具后，我们需要配置点数，以及最小和最大频率。我们还需要配置发生器将产生的信号幅度。在这种情况下，我的滤波器的固有频率是 3 kHz，所以如果幅度为 1V，频率范围为 500 Hz 到 10 kHz，我将使用配置。点数将配置频率步长。就我而言，我已根据需要更改了点数。

首先，我将双二阶滤波器配置为带阻巴特沃斯滤波器，固有频率为 3 kHz。这次我没有纠正频率扭曲。然后，单击 Single，ADC 5250 将执行一个完整的交换。结果如下图所示。

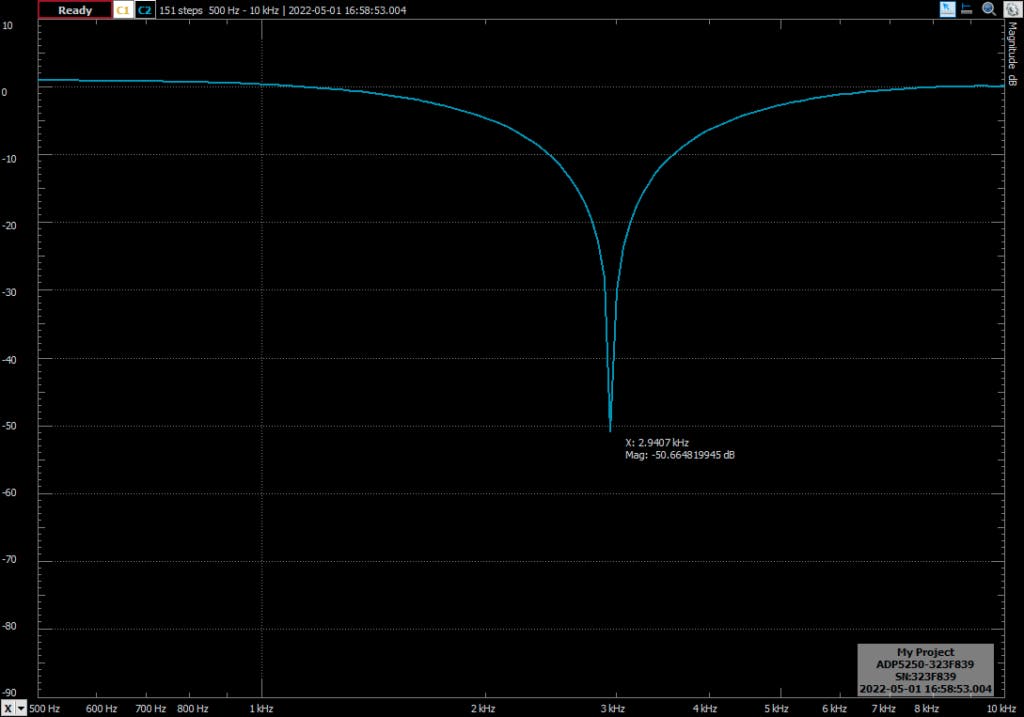
您可以看到滤波器的响应如何是预期的，但自然频率为 2.9407 khz，比预期频率低 59.3 Hz。对频率应用预变形，滤波器的响应是下一个（注意图像的缩放不同）。

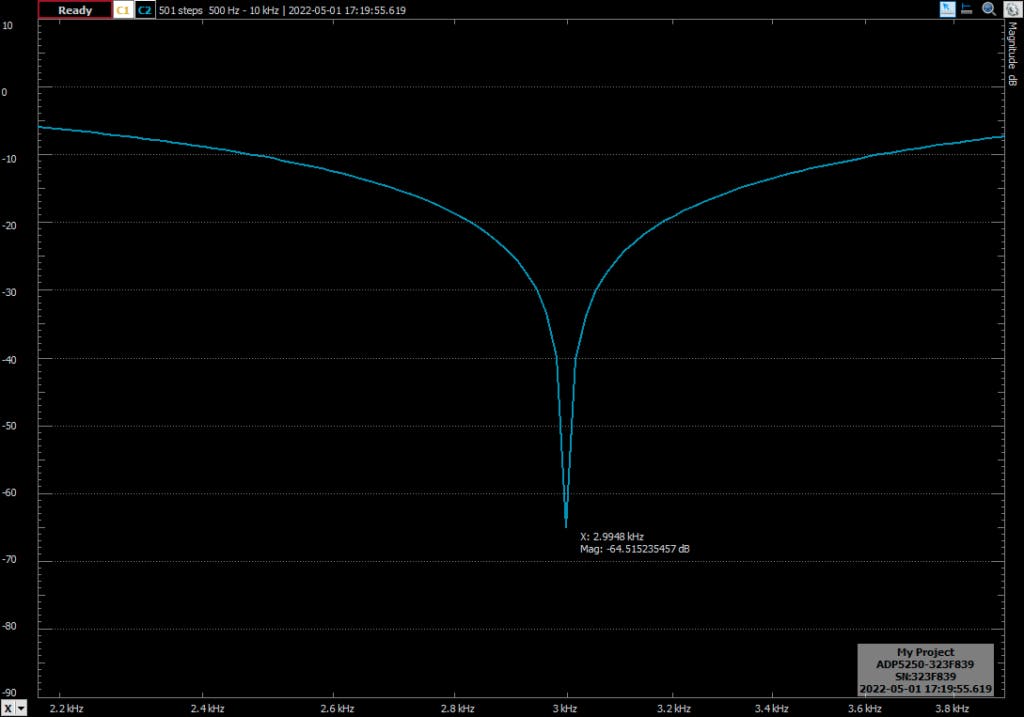
通过频率校正，误差如果为0.0052 Hz，这是一个卑鄙的误差。在接下来的测试中，我将滤波器的品质因数增加到 5。这将对陷波的带宽产生影响，从而获得更窄带的滤波器。

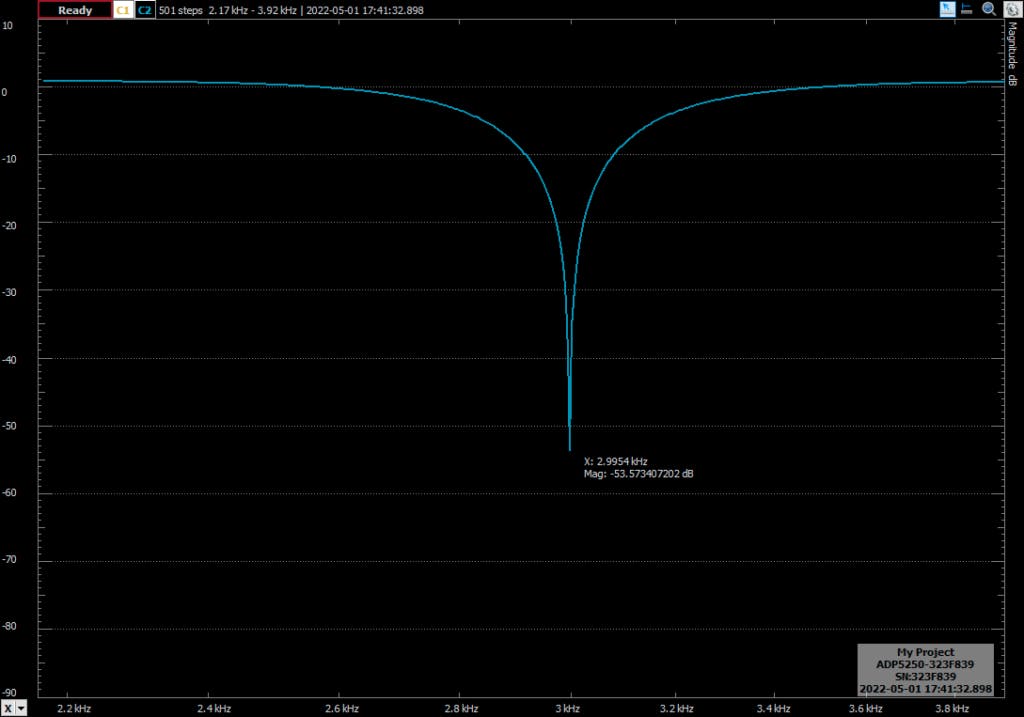
双线性变换因其简单性而被广泛用于设计 IIR 滤波器。我们只需要用 z 函数替换连续传递函数中的 s。其他方法如脉冲不变性需要部分分数展开代数，所以过程有点复杂。此外，双线性变换映射整个 s 平面，因此没有混叠误差。另一方面，它会在频率上产生扭曲，但使用预扭曲，正如我们在这篇文章中看到的，我们可以修复该频率偏差。