CUDA与Jetson Nano:并行Pollard Rho测试

描述

数学很难。当你的老师不喜欢教它时。

根据维基百科，

CUDA （Compute Unified Device Architecture）是由Nvidia创建的并行计算平台和应用程序编程接口（API）模型。它允许软件开发人员和软件工程师使用支持 CUDA 的图形处理单元 (GPU) 进行通用处理——一种称为 GPGPU（图形处理单元上的通用计算）的方法。CUDA平台是一个软件层，可直接访问 GPU 的虚拟指令集和并行计算元素，以执行计算内核。

CUDA （Compute Unified Device Architecture）是由Nvidia创建的并行计算平台和应用程序编程接口（API）模型。它允许软件开发人员和软件工程师使用支持 CUDA 的图形处理单元 (GPU) 进行通用处理——一种称为 GPGPU（图形处理单元上的通用计算）的方法。CUDA平台是一个软件层，可直接访问 GPU 的虚拟指令集和并行计算元素，以执行计算内核。

换句话说，英伟达提供了一个新的开发框架，由硬件和软件组成，用于并行计算任务，从而减少完成时间。

CUDA 范例由具有多个处理器的专用硬件和 C/C++ 语言的巧妙扩展组成，能够通过简单的任务来处理每个处理器的功能。当您必须执行搜索、查询、排序和卷积等重复性任务时，您可以（部分）摆脱繁重的循环，并将一小部分操作安排给不同的工作人员。由于数千个工作线程并行运行，完成任务的时间大大减少。

当然也有一些注意事项：虽然串行冯诺依曼调度只需要一个输入、一个在指令后完成详细说明的黑盒和一个输出，但并行架构需要考虑数据存储在哪里，谁在处理它（以及如何），一些数据何时可以免费用于下一次评估。并发分析并不容易，但是一旦你知道了基础，它就变得简单了。

CUDA 硬件 – Jetson Nano

CUDA 迎来了它的第 10 个化身，展示了作为一个强大而稳定的开发工具。CUDA 作为一种图形架构诞生，能够在显示器上快速处理像素并驱动其颜色，如今已成为一个完整的并行开发系统。虽然它的名气仍然存在于图形数据处理和成像领域，但越来越多的开发人员投入时间和精力来揭示和利用隐藏在裸机中的并行能力。工程师和数学研究人员重构了众所周知的串行算法，以利用多处理的惊人速度。

没错。我们开发了一种带有 CUDA GPU 的并行分解算法，比原始 CPU 方法快 1,000 倍。只需将一个线程专用于 960 个残差类（共 4620 个）中的每一个，我们就有了如此巨大的加速。但是Jetson Nano没有 960 个备用计算单元，虽然它仍然可以从 128 个 CUDA 内核中受益，但我们将在其上测试不同的分解算法。

我们将尝试一种完全不同的方法，而不是使用 125 cu 将工作细分为 8 个块，但确定性稍差，但这将利用Jetson Nano使用统计模拟的有限 CUDA。

 

分解——Pollard Rho 算法

来自维基百科：

假设我们需要分解一个数 n = p*q，其中 p 是一个非平凡的因子。一个多项式模 n，称为 g(x)（例如，g(x) = (x2 + 1) mod n，用于生成伪随机序列。选择一个起始值，比如 2，序列继续为 x1 =g(2), x2=g(g(2)), x3=g(g(g(2))) 等。该序列与另一个序列{xk mod p}有关。由于事先不知道p ，这个序列在算法中是无法明确计算的，但算法的核心思想就在其中。

因为这些序列的可能值的数量是有限的（模运算保证了它），所以 {xk} 序列（即 mod n）和 {xk mod p} 序列最终都会重复，即使我们不知道后者. 假设序列表现得像随机数。由于生日悖论（我们将在另一篇文章中分析），重复发生之前的 xk 的数量预计为 O(√N)，其中 N 是可能值的数量。所以序列 {xk mod p} 可能会比序列 {xk} 更早地重复。一旦一个序列有一个重复的值，这个序列就会循环，因为每个值只依赖于它之前的值。这种最终循环的结构产生了“Rho 算法”的名称，因为当值 x1 mod p、x2 mod p 等时，它与希腊字符 ρ 的形状相似。

假设我们需要分解一个数 n = p*q，其中 p 是一个非平凡的因子。一个多项式模 n，称为 g(x)（例如，g(x) = (x2 + 1) mod n，用于生成伪随机序列。选择一个起始值，比如 2，序列继续为 x1 =g(2), x2=g(g(2)), x3=g(g(g(2))) 等。该序列与另一个序列{xk mod p}有关。由于事先不知道p ，这个序列在算法中是无法明确计算的，但算法的核心思想就在其中。
因为这些序列的可能值的数量是有限的（模运算保证了它），所以 {xk} 序列（即 mod n）和 {xk mod p} 序列最终都会重复，即使我们不知道后者. 假设序列表现得像随机数。由于生日悖论（我们将在另一篇文章中分析），重复发生之前的 xk 的数量预计为 O(√N)，其中 N 是可能值的数量。所以序列 {xk mod p} 可能会比序列 {xk} 更早地重复。一旦一个序列有一个重复的值，这个序列就会循环，因为每个值只依赖于它之前的值。这种最终循环的结构产生了“Rho 算法”的名称，因为当值 x1 mod p、x2 mod p 等时，它与希腊字符 ρ 的形状相似。

好的。现在让我们深吸一口气，看看上一段的真正含义。

假设我们在一条长长的圆形赛道上跑步。我们怎么知道我们已经完成了一个周期？一个聪明的解决方案是让两个跑步者 A 和 B 跑得比 A 快两倍。他们从同一个位置开始，当 B 超过 A 时，我们知道 B 至少循环了一次。

我们有以下算法：

x = 2; y = 2; d = 1
while d == 1:
x = g(x)
y = g(g(y))
d = gcd(|x - y|, n)
if d == n:
return failure
else:
return d

假设我们想分解数字 8051。我们有

n = 8051
x = 2
y = 2
g(x) = (x^2 + 1)
g(g(x)) = g(x^2 + 1)

应用该算法，我们得到以下解决步骤：

迭代示例

 

从不同的 x 和/或 y 开始，我们可以找到 8051、83 的另一个除数

如果我们使用朴素的试因式分解算法，我们应该测试 N 的平方根以下的所有质因数。试制因式算法随着数字 (2n/2) 的位数呈指数增长。

Pollard Rho 算法在其运行时间和它找到一个因子的概率之间提供了一种权衡。在 O(√d) <= O(n1/4) 次迭代中，可以以大约 0.5 的概率实现素数除数。这是一个启发式的主张，对算法的严格分析仍然是开放的。

从理论到实践

为了展示实际的算法（以及并行实现如何加速结果），我们准备了一个简短的源代码，使用一个 CPU、通过 OpenMP 的多个 CPU 和 GPU 运行 Pollard Rho 分解。提供了要分解的候选者列表，以显示：

• 随着因子的增长，算法如何变慢
• 放缓是如何归因于因子大小，而不是因子数量
• GPU 开销如何使并行算法在较小的因素上比 CPU 慢
• 正确选择 GPU 的块大小和块数如何带来更好的结果
• 并行算法的整体增益是多少。

 

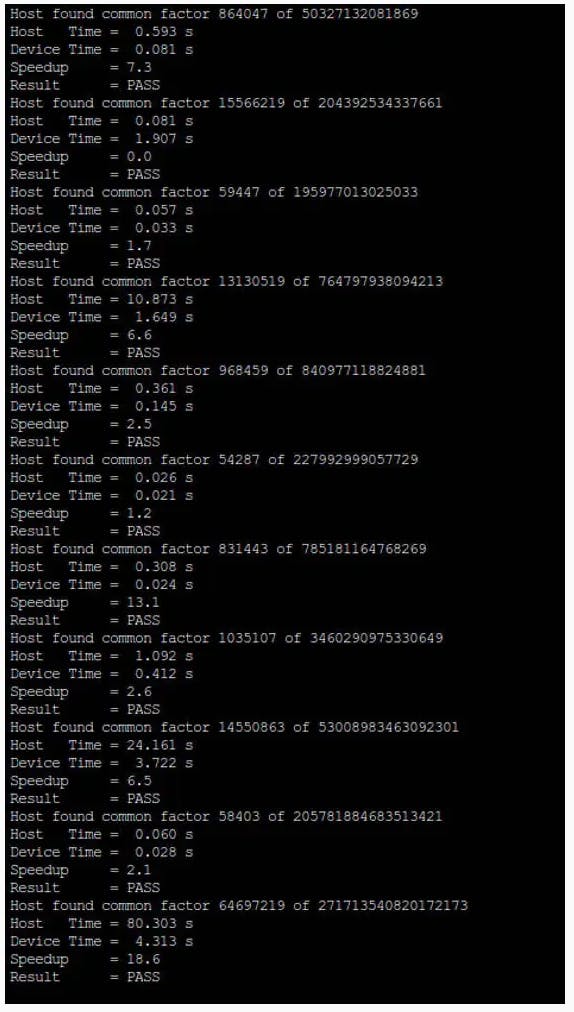
我们提出的算法仅限于 64 位数字，但很容易将其扩展到多精度算术。无论如何，众所周知，Pollard Rho 的效率随着因子的长度而降低：一般情况下，当 N 超过 40 位时，应选择其他方法（如 P-1 和 ECM）。

该算法对于具有小因子的数字非常快，但在所有因子都很大的情况下较慢。The ρ algorithm's most remarkable success was the factorization of the eighth Fermat number , F 8 = 1238926361552897 * 93461639715357977769163558199606896584051237541638188580280321. The ρ algorithm was a good choice for F 8 because the prime factor p = 1238926361552897 is much smaller than the other factor. UNIVAC 1100/42 的分解耗时 2 小时。

您可以在我的FermatSearch网站上找到有关费马分解和素数证明的更多信息。

CPU和GPU实现的区别

我们有两个不同的内核作为主机和设备运行。

主机内核在 CPU（或启用 OpenMP 时的 CPU）上运行。它需要对数字进行分解，然后循环直到找到解决方案。

设备内核在 GPU 上运行。x 和 y 的（随机）值被预先计算、索引并存储在数组中。数组在要分解的数字之后异步复制。然后启动块。设备代码的每个线程同时访问数组的一部分，计算其步长 (g(x), g(g(x)), 和的绝对值和 gcd)，然后将结果存储回数组中，然后检查 GCD 是否大于 1。如果是，我们有一个因子。该值保存在结果位置。一旦这个单程循环完成，结果就会被传送回主机内存，并返回给调用主程序。

它的表现如何？

我们使用了 19 个数字的列表，并在 2 个不同的平台上对它们进行了测试：一台配备Intel Core i7 9800X处理器和Nvidia RTX 2060 GPU的 PC ，以及 Nvidia Jetson Nano板。

PC给出了以下结果：

Overall results:
Host   Time = 503.134 s
Device Time =   1.576 s
Speedup     = 319.2

换句话说，即使是 CUDA 中算法的简单实现也显示出 320 倍的加速。当我们有 1920 个计算单元时，我们在 GPU 上运行 256×256 网格，并且没有利用共享内存加速或寄存器优化。

在 Nano 上，我们实现了以下时序：

Overall results:
Host   Time = 1893.795 s
Device Time =   39.448 s
Speedup     =   48.0

Nano 上的 GPU 是 Maxwell，具有少量内核和低于 1 GHz 的时钟，但相对于 CPU，我们实现了 48 倍的加速。

我们还注意到，使用并行算法的 Jetson Nano 的 CUDA 比Intel 9800X 快 12 倍以上。对于成本比 PC 系统低 15 倍的电路板来说还不错。

Github上提供了使用 Jetson Nano 试验 CUDA 的源代码。我们将很快测试其他背靠背 CPU vs GPU 算法，不仅展示并行计算的乐趣，也展示 CUDA 图形加速的惊人之处。