完善资料让更多小伙伴认识你,还能领取20积分哦,立即完善>
标签 > LDPC

LDPC是Low Density Parity Check Code英文缩写,意思是低密度奇偶校验码,最早在20世纪60年代由Gallager在他的博士论文中提出。
LDPC码最早在20世纪60年代由Gallager在他的博士论文中提出,但限于当时的技术条件,缺乏可行的译码算法,此后的35年间基本上被人们忽略,其间由Tanner在1981年推广了LDPC码并给出了LDPC码的图表示,即后来所称的Tanner图。1993年Berrou等人发现了Turbo码,在此基础上,1995年前后MacKay和Neal等人对LDPC码重新进行了研究,提出了可行的译码算法,从而进一步发现了LDPC码所具有的良好性能,迅速引起强烈反响和极大关注。经过十几年来的研究和发展,研究人员在各方面都取得了突破性的进展,LDPC码的相关技术也日趋成熟,甚至已经开始有了商业化的应用成果,并进入了无线通信等相关领域的标准。LDPC码是通过校验矩阵定义的一类线性码,为使译码可行,在码长较长时需要校验矩阵满足“稀疏性”,即校验矩阵中1的密度比较低,也就是要求校验矩阵中1的个数远小于0的个数,并且码长越长,密度就要越低。
LDPC是Low Density Parity Check Code英文缩写,意思是低密度奇偶校验码,最早在20世纪60年代由Gallager在他的博士论文中提出。
发展历史
LDPC码最早在20世纪60年代由Gallager在他的博士论文中提出,但限于当时的技术条件,缺乏可行的译码算法,此后的35年间基本上被人们忽略,其间由Tanner在1981年推广了LDPC码并给出了LDPC码的图表示,即后来所称的Tanner图。1993年Berrou等人发现了Turbo码,在此基础上,1995年前后MacKay和Neal等人对LDPC码重新进行了研究,提出了可行的译码算法,从而进一步发现了LDPC码所具有的良好性能,迅速引起强烈反响和极大关注。经过十几年来的研究和发展,研究人员在各方面都取得了突破性的进展,LDPC码的相关技术也日趋成熟,甚至已经开始有了商业化的应用成果,并进入了无线通信等相关领域的标准。LDPC码是通过校验矩阵定义的一类线性码,为使译码可行,在码长较长时需要校验矩阵满足“稀疏性”,即校验矩阵中1的密度比较低,也就是要求校验矩阵中1的个数远小于0的个数,并且码长越长,密度就要越低。
应用热点
LDPC码即低密度奇偶校验码(Low Density Parity Check Code,LDPC),它由Robert G.Gallager博士于1963年提出的一类具有稀疏校验矩阵的线性分组码,不仅有逼近Shannon限的良好性能,而且译码复杂度较低, 结构灵活,是近年信道编码领域的研究热点,目前已广泛应用于深空通信、光纤通信、卫星数字视频和音频广播等领域。LDPC码已成为第四代通信系统(4G)强有力的竞争者,而基于LDPC码的编码方案已经被下一代卫星数字视频广播标准DVB-S2采纳。
译码算法
对同样的LDPC码来说,采用不同的译码算法可以获得不同的误码性能。优秀的译码算法可以获得很好的误码性能,反之,采用普通的译码算法,误码性能则表现一般。LDPC码的译码算法包括以下三大类:硬判决译码,软判决译码和混合译码。1. 硬判决译码将接收的实数序列先通过解调器进行解调,再进行硬判决,得到硬判决0,1序列,最后将得到的硬判决序列输送到硬判决译码器进行译码。这种方式的计算复杂度固然很低,但是硬判决操作会损失掉大部分的信道信息,导致信道信息利用率很低,硬判决译码的信道信息利用率和译码复杂度是三大类译码中最低的。常见的硬判决译码算法有比特翻转(bit-flipping, BF)算法、一步大数逻辑(one-step majority-logic, OSMLG)译码算法。2. 软判决译码可以看成是无穷比特量化译码,它充分利用接收的信道信息(软信息),信道信息利用率得到了极大的提高,软判决译码利用的信道信息不仅包括信道信息的符号,也包括信道信息的幅度值。信道信息的充分利用,极大地提高了译码性能,使得译码可以迭代进行,充分挖掘接收的信道信息,最终获得出色的误码性能。软判决译码的信道信息利用率和译码复杂度是三大类译码中最高的。最常用的软判决译码算法是和积译码算法,又称置信传播 (belief propagation, BP)算法。3. 与上述的硬判决译码和软判决译码相比,混合译码结合了软判决译码和硬判决译码的特点,是一类基于可靠度的译码算法,它在硬判决译码的基础上,利用部分信道信息进行可靠度的计算。常用的混合译码算法有、加权比特翻转(weighted BF, WBF)算法、加权OSMLG(weighted OSMLG, WMLG)译码算法。
LDPC初级之Decoder基础
LDPC (Low-Density Parity-Check,低密度奇偶校验) 强大的纠错能力使其应用范围越来越广。LDPC可以简单的分成编码器(Encoder),信道模型(Channel model),解码器(Decoder)三部分。其中Decoder在这三部分中最为简单,为此,初级系列先介绍decoder,便于大家对LDPC有一个初步的了解。
如今LDPC的Decoder多采用sum-product decoding。而在介绍sum-product之前,有必要先介绍message-passing和bit-flipping decoding,了解它们对于了解sum-product,以及后续深入学习LDPC有很大的帮助。
Tanner Graph
直观认识message-passing工作原理的最佳工具是Tanner Graph。每个parity-check matrix H都有一个对应的Tanner Graph。以一个例子说明Tanner Graph的构造原理,如下H矩阵:
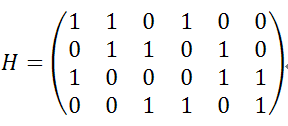 (1)
(1)
H阵的每一行对应的都是一个parity-check,将第m行中每个“1”所处的第n列,即bit cn,归纳成一个组合
比如, ,
.因此,第m行的parity-check可以表述成:
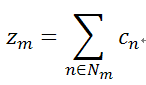
其中是第m行中元素。
同时,定义
![]()
为第m行中除了第n列,其它元素为“1”的列。比如, ,
.
除了组合每行中的元素“1”的列位置,还需组合每列中元素“1”所处的行位置。定义:
![]()
为第n列(bit cn)所处元素为“1”的行。比如, ,
.
定义:
![]()
为第n列中除了第m行,其它对应元素为”1”的行。如:, .
了解这些,除了对创建Tanner Graph有帮助外,还对了解后续的bit-flipping, sum-product等帮助。
Tanner Graph由三种元素构成:
- bit nodes:代表H阵中的列,也就是codeword的每个bit;
- check nodes:代表H阵中的行,也就是parity-check约束;
- edge:如果Hmn=1,则第n个bit node和第m个check node之间会互连,即一条edge。
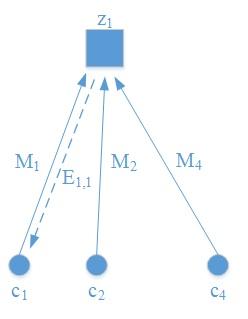
根据以上的H矩阵,其对应的Tanner Graph如下图:
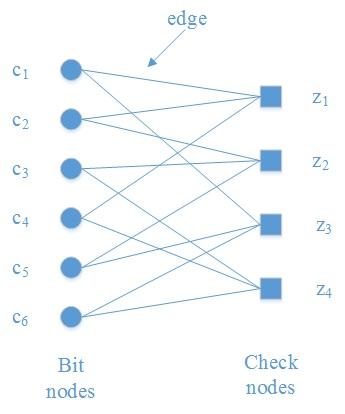
因为, 则check node z1与c1, c2, c4之间有edge。因为
,则bit node c1与z1, z3之间有edge。
Message-Passing
Message-passing是指信息在相连的check nodes和bit nodes间传递。Bit-flipping和sum-product decoding都属于message-passing,所不同的是,二者传递的信息不一样。下面以BEC(Bit Erasure Channel)为例,介绍message-passing的工作原理,让大家对其有一个直观的了解。
所谓BEC,是指在其通道中传输的信号要么被接收器正确的接收,要么被通道erase掉,使得接收器没有接收到此信号。由于接收到的信号都是正确的,因此Decoder只需要处理那些没有接收到的未知信号即可。
回想Decoder判断接收信号为codeword的基本原理,
以H阵的z1为例,则需满足如下关系
![]()
假设bit c1=r1=”0”,c2=r2=”1”,c4在经过BEC通道时出错,导致r4未知:r4=”x”,则可以推断出c4=“1”,由此完成对c4在纠错。因此,BEC的message-passingdecoding可以简化如下:
1. 初始化:接收到信号(”x”代表对应bit被BEC erase)视为由bit nodes传递给相连check nodes的初始信息。
2. check nodes update: 如果传递到check node zm的信息中没有”x”,则check nodes无需生成新信息;如果只有cn=”x”,则需根据
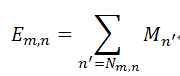
其中为mod 2求和,
为check node zm生成的信息,并将其传递给bit cn。如果有两个及以上的bit node为”x”,则zm无法纠错,
.
3. bit nodes update: 如果bit nodes的状态为”x”,则将其更新为接收到的信息。
4. 如果bit nodes没有了”x”,则decoding结束;否则从步骤2处开始,继续迭代。
Example:
由方程(1)中的H矩阵,编码得到一个codeword c=[0 0 1 0 1 1]。经过BEC通道后,接收到的信号r=[0 0 1 x x x]。 Message-passing decoding的纠错过程如下:
1. 初始化:bit nodes传递给check nodes的初始信息M=[0 0 1 x x x]。
2. Check nodes update:
由H矩阵及其Tanner Graph可知,z1与c1, c2, c4相连,其中M4=”x”,则check nodez1生成信息
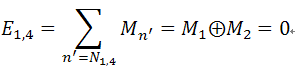
z2与c2, c3, c5相连,其中M5=”x”,则check nodez2生成信息
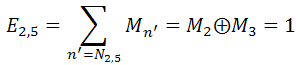
z3与c1, c5, c6相连,其中M5=”x”,M6=”x”。因为有两个未知信息,所以check nodez3无法纠错,因此z3生成信息
![]()
z4与c3, c4, c6相连,其中M4=”x”,M6=”x”。则
![]()
3. Bit nodes update
因为M4=”x”,,则Bit node c4=”0”。
因为M5=”x”,, 则Bit node c5=”1”。
因为M6=”x”, ,,则Bit node c6=”x”。
Bit nodes update结束后,各Bit node的信息更新为M=[0 0 1 0 1 x]。因此重复Check nodes update,继续迭代。
4. Check nodes update
z3与c1, c5, c6相连,其中M6=”x”。则
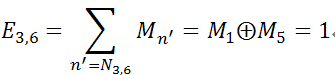
z4与c3, c4, c6相连,其中M6=”x”。则
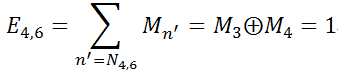
5. Bit nodes update
目前只有M6=”x”, , 则Bit node c6的信息更新为1,M=[0 0 1 0 1 1]。
6. End
至此,所有bit nodes的信息都为0/1,不再有”x”,纠错结束。
通过以上的分析,想必大家对message-passing decoding中的message和passing有了直观的了解。BEC的特性决定了接收到的信息一定是正确的,所以其decoding的方法只是syndrome decoding。但是在BSC (Binary Symmetric Channel)和AWGN (Additive White Gaussian Noise)通道中,由于接收到的数据并不能明确知道其对错,导致decoding的方法会与BEC有所不同。
尽管BEC的message-passing decoding方法非常简单,但是其中也存在缺陷。请大家思考一个问题:什么情况下,无论进行多少次的迭代计算,BEC的message-passing decoding依然无法纠错成功?后续的文章中会对此做专题分析。
Bit-Flipping Decoding
Bit-flipping是message-passing中的hard-decision算法,在bit nodes 和check nodes中,传递的信息是0/1。Check node依然利用syndrome decoding的方法来生成信息。与BEC中的message-passing decoding不同的是,由于每个接收到的bit信息都存在出错的可能性,所以check nodes需要针对每个与之相连的bit node生成信息。具体decoding步骤如下:
1. 初始化:接收到信号视为由bit nodes传递给相连check nodes的初始信息。
2. check nodes update: check node zm根据接收到的信息,针对每个与之相连的bit node生成信息
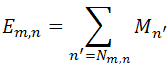
其中 为mod 2求和。
3. bit nodes update: bit node接收与之相连的check nodes传递来的信息。如果接收到的大部分信息与原bit node值不同,则bit node值翻转。
4. 如果bit nodes的值满足syndrome decoding,则decoding成功;否则从2开始继续迭代。
Example:
由方程(1)中的H矩阵,编码得到一个codeword c=[0 0 1 0 1 1]。经过BSC通道后,接收到的信号r=[1 0 1 0 1 1]。 Bit-flipping decoding的纠错过程如下:
1. 初始化:bit nodes传递给check nodes的初始信息M=[1 0 1 0 1 1]。
2. Check nodes update: check node z1接收来自bit node c1, c2, c4的信息,则
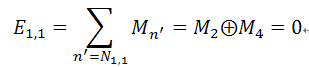
即反馈给c1的信息, 如下图所示。
反馈给c2的信息
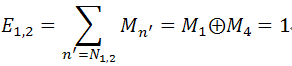
反馈给c4的信息
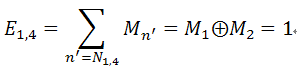
同理,依次计算出:
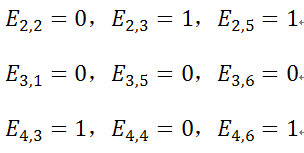
3. Bit nodes update:
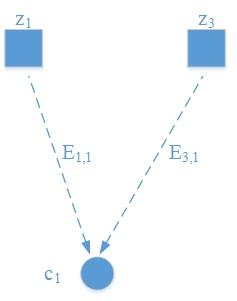
bit node c1与check nodes z1,z3相连,如下图所示。, 而
。根据服从大多数的原则,c1的信息要翻转,则
;
bit node c2与check nodes z1,z2相连,
![]()
不满足大多数的原则,保持不变;
bit node c3与check nodes z2,z4相连,
![]()
则保持不变;
bit node c4与check nodes z1,z4相连,
![]()
保持不变;
bit node c5与check nodes z2,z3相连,
![]()
保持不变;
bit node c6与check nodes z3,z4相连,
![]()
保持不变。
Bit nodes update完成后,M=[0 0 1 0 1 1]。
4. 验证M是否满足syndrome decoding.
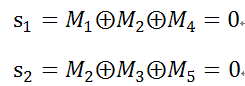
同理,。因此纠错成功,c=[0 0 1 0 1 1]为发送codeword.
通过对BEC中的Message-passing decoding,以及Bit-flipping decoding的介绍,了解各decoding方法中的message和passing后,对于message-passing的工作过程及基本原理会有一个直观的影响。这对于掌握sum-product decoding会有很好的帮助。


为了早日实现5G,Qualcomm 积极致力于5G设计,以促进并加快其发展。想要真正让5G NR和 5G愿景变成现实,就不得不说五大关键无线发明。
LDPC码(低密度奇偶校验码)的校验矩阵具有非常强的稀疏性,也就是校验矩阵里面“0”占了大多数,“1”的数量极少。“1”元素的分布非常稀疏,...
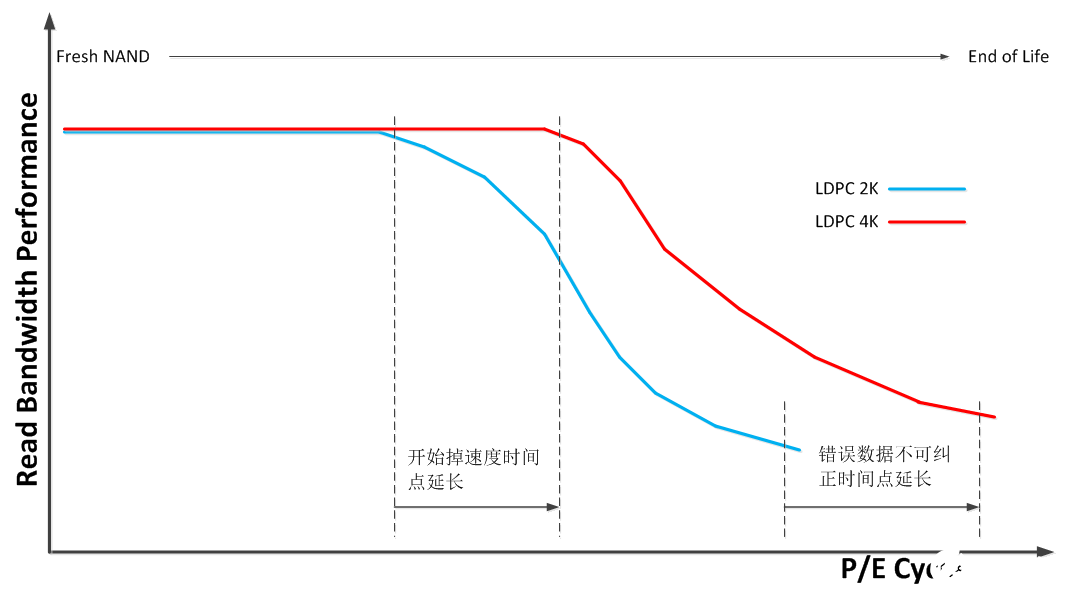
联芸成功实现基于4K LDPC纠错的第三代Agile ECC 3闪存信号处理技术的开发和验证 可极大延长NAND的使用寿命
追求存储密度以降低存储成本不断推动着NAND闪存技术的发展。NAND闪存技术已经从最初的SLC时代,跨越MLC、TLC向QLC时代快速演进,并且从最初的...
一种输出格式可控的多码率LDPC编码器实现 0 引 言 目前,LDPC码已广泛应用于深空通信、光纤通信、数字音视频广播等领域。由于有着较Turb...
AccelerComm推出完全集成的PUSCH解码器,为性能关键的信道加快5G NR
这一高度集成的解决方案基于公司的信道编码和调制/解调IP产品组合,使5G基站能够受益于AccelerComm一流的LDPC解码器性能,同时最大限度地缩短...
如今SSD固态硬盘早已不是什么新鲜事物,但是说起选购来,可能很多朋友并不清楚同样是1TB容量的SSD固态硬盘,在性能上到底有何差别,或许有些朋友能够说出...

国内首颗,精准纠错!德明利TWSC2985系列:支持4K LDPC技术的存储芯片
TWSC 2985 系列SD6.0存储芯片 国内首颗支持4K LDPC纠错技术 增强纠错、耐久可靠、性能升级 随着移动计算和AI技术对数据存储需求的...
编辑推荐厂商产品技术软件/工具OS/语言教程专题
| 电机控制 | DSP | 氮化镓 | 功率放大器 | ChatGPT | 自动驾驶 | TI | 瑞萨电子 |
| BLDC | PLC | 碳化硅 | 二极管 | OpenAI | 元宇宙 | 安森美 | ADI |
| 无刷电机 | FOC | IGBT | 逆变器 | 文心一言 | 5G | 英飞凌 | 罗姆 |
| 直流电机 | PID | MOSFET | 传感器 | 人工智能 | 物联网 | NXP | 赛灵思 |
| 步进电机 | SPWM | 充电桩 | IPM | 机器视觉 | 无人机 | 三菱电机 | ST |
| 伺服电机 | SVPWM | 光伏发电 | UPS | AR | 智能电网 | 国民技术 | Microchip |
| 开关电源 | 步进电机 | 无线充电 | LabVIEW | EMC | PLC | OLED | 单片机 |
| 5G | m2m | DSP | MCU | ASIC | CPU | ROM | DRAM |
| NB-IoT | LoRa | Zigbee | NFC | 蓝牙 | RFID | Wi-Fi | SIGFOX |
| Type-C | USB | 以太网 | 仿真器 | RISC | RAM | 寄存器 | GPU |
| 语音识别 | 万用表 | CPLD | 耦合 | 电路仿真 | 电容滤波 | 保护电路 | 看门狗 |
| CAN | CSI | DSI | DVI | Ethernet | HDMI | I2C | RS-485 |
| SDI | nas | DMA | HomeKit | 阈值电压 | UART | 机器学习 | TensorFlow |
| Arduino | BeagleBone | 树莓派 | STM32 | MSP430 | EFM32 | ARM mbed | EDA |
| 示波器 | LPC | imx8 | PSoC | Altium Designer | Allegro | Mentor | Pads |
| OrCAD | Cadence | AutoCAD | 华秋DFM | Keil | MATLAB | MPLAB | Quartus |
| C++ | Java | Python | JavaScript | node.js | RISC-V | verilog | Tensorflow |
| Android | iOS | linux | RTOS | FreeRTOS | LiteOS | RT-THread | uCOS |
| DuerOS | Brillo | Windows11 | HarmonyOS |