CDMA移动台功率控制与校准原理及设计
为了保证每一个CDMA移动台的射频指标都满足行业标准(3GPP2)的要求,保证CDMA网络的性能,必须对每部移动台进行射频校准。在进行射频校准算法论述之前,首先对CDMA移动台功率控制算法原理进行说明。CDMA移动台的射频电路存在大量的模拟器件,模拟器件具有很大的器件离散性。
RASRAM线性控制原理
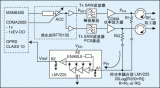
基带移动台功率控制算法采用RASRAM线性控制原理。由于中频(IF)AGC放大器线性度不好,增益衰减量与增益控制电压大小不成正比。换句话说,衰减的变化与控制电压的变化不成正比,衰减与增益控制电压函数非线性化。RAS (Rf Analog System)RAM linearizer产生可变的增益放大控制电压, 使Pulse Density Modulation(以下简称PDM) 驱动电路补偿上述非线性特性。RAS RAM linearizer是一个简单的转换函数,它通过一个可编程的分段线性函数,使校准后的RAS RAM linearizer输入和衰减线性化。
CDMA移动台射频校准算法
基准信道(功率控制的参考信道)的功率校准部份是整个CDMA移动台校准系统最基本最重要的部分,它的准确程度关系到整个系统的功率准确度。在各种功率校准算法中,业界普遍应用的算法主要有两种:功率迭代测量算法和线性拟合算法。下面分别介绍这两种算法的原理和在CDMA移动台功率校准中的实现过程。
1 线性拟合基本算法
线性拟合算法分为最优差补与外延两种算法,两种算法的计算数学模型都是一样的。下面以最优差补算法为例来介绍。
假定移动台理想输出功率数组为:
Table[i]=-66.8;-63.6;-60.4;-57.2;-54;-50.8;-47.6;-44.4;-41.2;-38;-34.8;-31.6;-28.4;-25.2;-22;-18.8;-15.6;-12.4;-9.2;-6;-2.8;0.4;3.6;6.8;10;13.2;16.4;18;19.6;21.2;22.8;24.4;26;27.6;
29.2;30.8;32.4;34;35.6;37.2;38.8;40.4;42;45.2;48.4;单位:dBm。
对于每一个理想输出功率测试点来说,理想输出功率Table[i]确定后,即可通过其他最近相邻功率测试点插值求出PDM的补偿值。
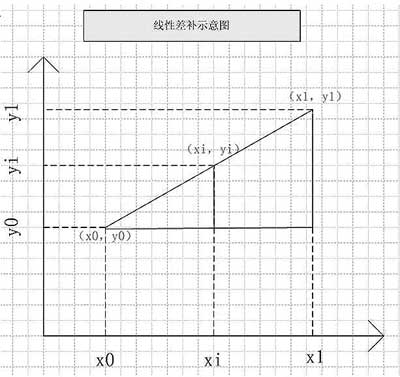
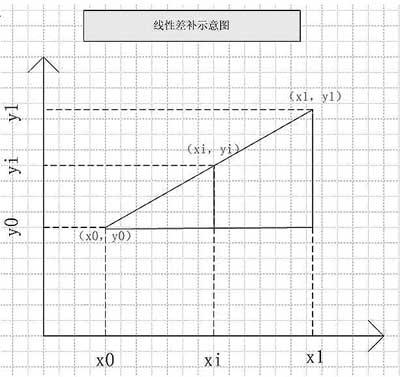
图1 线性差补法
由图1可知,
Yi-y0=K (xi-x0)=(y1-y0)/(x1-x0)*(xi-x0) (1)
将y0移到右边得,
Yi=K (xi-x0)=( y1-y0)/(x1-x0)*(xi-x0)+y0 (2)
已知Yi=Table[i], y1、y0为最近相邻测试功率值,x0、x1为最近相邻测试点的测试功率对应PDM值,xi即为所求理想输出功率的对应PDM值。
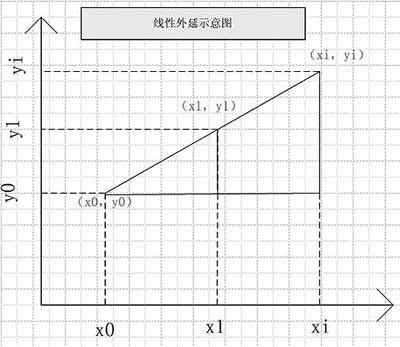
图2 线性外延法
如果所求理想输出功率电平落在测试功率电平的范围之外,那么需要用如图2所示外延方法计算,原理同上,不再赘述。
2 线性拟合实现过程
首先把CDMA输出功率等级分为高功率等级和低功率等级两组。在每一组中按照功率控制的动态范围分为若干个测试点,测试过程中测试各个点得出对应的功率控制管脚的电压(对应PDM值)和功率放大器输出功率的数值,然后通过线性拟合得出在该功率等级上的功率控制管脚的电压和功率放大器输出功率之间的近似线性关系。
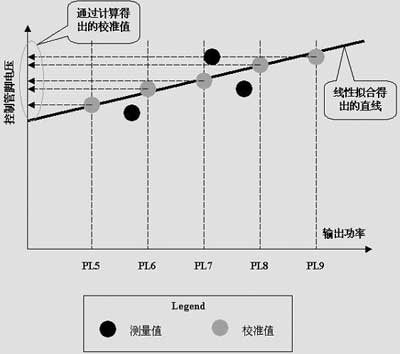
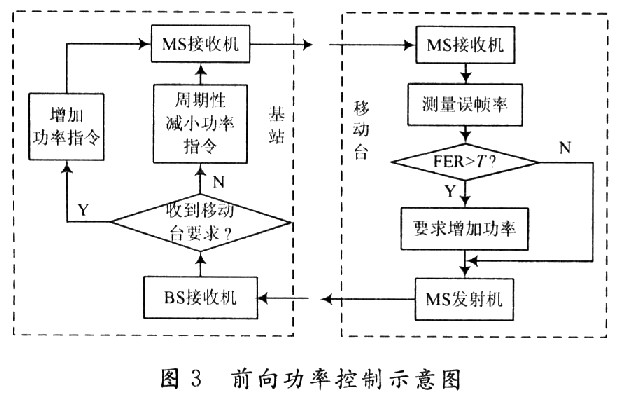
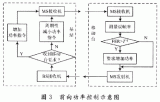
图3 实际生产中采用的一种校准算法
最后再根据该功率等级组中不同功率等级所需要的理想输出功率计算出所对应的功率控制管脚的电压值。
这一校准过程需要在高、低二个功率等级上分别进行。最多时可以测试多达64个点。经过上述校准以后的CDMA移动台,其发射功率的精度可以达到 ±0.4dB左右。
3 线性拟合特点
优点:每个功率点校正仅进行一次测量,校准速度较快,生产节拍快,生产成本低。
缺点:如果测量的功率值没有落在最优差补的区间范围内,由于模拟射频硬件的阴极特性,功率电压曲线是非线性的,但是程序算法会按照线性外延算法计算,因而导致计算值与理想的功率值存在较大的精度差距,测试精度较低。
4 功率迭代测量基本算法
移动台功率电压的特性曲线可以看作是一个非线性函数。一个非线性函数的功率电压特性曲线可以通过划分成36个小段的曲线来拟合,而每一段可以看作是一线性关系的函数。
针对不同的功率曲线线段的特性,为了提高收敛速度,增加收敛因子K的概念,将上述CDMA功率的功率迭代测量公式转化为分段迭代公式,参数实例化如下:
X1(n+1)-X1(n)=(int)4*(Y1(n)-Ynd) 初值Xd为物理特性为驱动电压值。 Xd[36]={100,120,140,170,……460,480} Ynd为理想输出功率为。 Ynd[36]={48.4,45.2;42,38.8,35.6,32.4,29.2,26,22.8,19.6,16.4,13.2,10,6.8,3.6,0.4, 其中,单位为dBm,收敛因子K=3、4、5、6。 迭代算法是用计算机解决问题的一种基本方法。它利用计算机运算速度快、适合做重复性操作的特点,让计算机对一组指令(或一定步骤)进行重复执行,在每次执行这组指令(或这些步骤)时,都从变量的原值推出它的一个新值。但利用迭代算法解决问题,需要有以下三步。 确定迭代变量。在可以用迭代算法解决的问题中,至少存在一个直接或间接地不断由旧值递推出新值的变量,这个变量就是迭代变量。 建立迭代关系式。所谓迭代关系式,指如何从变量的前一个值推出其下一个值的公式(或关系)。迭代关系式的建立是解决迭代问题的关键,通常可以使用递推或倒推的方法来完成。 对迭代过程进行控制。在什么时候结束迭代过程?这是编写迭代程序必须考虑的问题。不能让迭代过程无休止地重复执行下去。迭代过程的控制通常可分为两种情况:一种是所需的迭代次数是个确定的值,可以计算出来;另一种是所需的迭代次数无法确定。对于前一种情况,可以构建一个固定次数的循环来实现对迭代过程的控制;对于后一种情况,需要进一步分析出用来结束迭代过程的条件。对于要实现移动台的功率校正功能算法来说,属于后一种情况,迭代中止规则通常采用fabs(Y(n)-Yd) <ε(其中ε>0,是设定的相对误差容限)。这里,根据测试系统的系统误差,我们取ε=0.2dB。 根据PA的电路驱动原理,在某一段特性曲线内,输出功率对PA输入电压可以近似看作K倍的线性关系,因此可有△x=K△y+θ,也就是说:X(i+1)-X(i)=K(Y(i)-Y(d))+θ,θ是一个固定的常数。我们可以将此作为迭代公式,运用计算机求对应某个功率的准确电压值(在一定的迭代精度ε前提条件下)。 单点功率三次迭代过程如图4所示。 图4 迭代算法原理 显然,单点迭代次数受收敛因子K的影响很大,K越大,迭代次数越少,但是迭代精度越低;相反,K越小,迭代次数越多,但是迭代精度越高。 根据以上分析,对于每个功率点,实现CDMA功率迭代测量公式可以用数学语言描述如下: X(n+1)-X(n)=(int)K*(Y(n)-Yd) K是收敛因子,Y(n) 是移动台发送X(n) PDM值时由测量仪表测量获得;Yd是移动台功率电压曲线为线性时发送的理想输出功率。 初始条件:X(0)=Xd Xd是移动台的迭代发送PDM初始值。 5 功率迭代测量实现过程 把CDMA输出功率等级分为二组:高功率等级和低功率等级。在每一组中按照功率控制的动态范围分为若干个测试点。 测试过程中,首先根据该功率等级组中选定的不同功率测试点所需要的理想输出功率,采用功率迭代测量算法逐步发送PDM,并测量发出的功率值,直到达到理想输出功率为止,然后将得到的PDM写入计算链表。 根据计算链表,结合未选择的不同功率等级所需要的理想输出功率,通过插补与外延得出在该功率等级上的功率控制管脚的电压和功率放大器理想输出功率之间的对应计算链表。 为了能够满足CDMA移动台功率控制精度要求。这一校准过程需要在高、低二个功率等级上分别进行。经过上述校准以后的CDMA移动台,其发射功率的精度可以控制在系统的测试误差范围之内。 6 功率迭代测量特点 特点:校准速度较慢,生产成本高,精度较高。 优点:由于测量值与理想输出功率之间的误差可以通过调整相对误差容限来控制,因此测试精度可以控制的比较高(最好情况下,控制在测试系统的系统误差内),也可以控制比较低。 缺点:每个功率点测量因为选择的迭代因子K不同,导致迭代次数或多或少,并且每个点至少进行一次功率测量,因此校准速度较慢,生产节拍慢,会占用较多的宝贵生产仪表测试资源,因此生产成本比较高。 结束语 综上所述,功率迭代测量算法和线性拟合算法各有利弊。鉴于CDMA系统功率控制精度按照1dB的步长控制移动台的功率变化精度,同时考虑移动台测试校准的生产成本,结合线性拟合算法速度快,并且校准精度也满足系统要求,因此,在生产和研发工程实践中,一般选择线性拟合算法实现CDMA移动台的生产功率校正算法。
(Y1(n)-Y1d)<4, Y1(n)<17dbm, 0
(Y2(n)-Y2d)>=4,Y2(n)<17dbm,0
(Y3(n)-Y3d)<3,Y3(n)>=17dbm,0
(Y4(n)-Y4d)>=3,Y4(n)>=17dbm,0
-2.8,-6,-9.2,-12.4,-15.6,-18.8,-22,-25.2,-28.4,-31.6,-34.8,-38,-41.2,-44.4,-47.6,-50.8,-54,-57.2,-60.4} 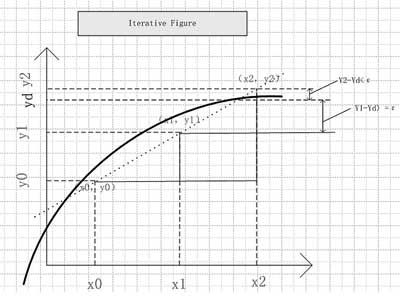
第一次迭代:X0=Xd,Y0-Yd>ε,不满足|Y0-Yd|<ε迭代停止条件,继续迭代;
第二次迭代:X1=X0,Y1-Yd>ε,不满足|Y0-Yd|<ε迭代停止条件,继续迭代;
第三次迭代:X2=X1,Y2-Yd<ε,满足|Y0-Yd|<ε迭代停止条件,停止迭代;X2即为所求的PA输入电压值(迭代精度ε前提条件:ε=0.2dB)。
 电子发烧友App
电子发烧友App






















评论