Rotman透镜多波束形成网络的数值分析
本文利用平板波导模型法与轮廓积分方程法结合分析了一种重要的多波束形成网络—Rotman透镜.首先建立了考虑色散效应的透镜的等效平板波导模型,然后选择适当的波导模式函数展开透镜端口上的场,并利用Galerkin法求解其边缘上电场满足的轮廓积分方程即可得到透镜的多模式散射参数.再根据网络思想,将端口存在的高阶模作为加载.从而得到主模激励的散射参数,计算结果与实验结果吻合得很好.
关键词:多波束网络;Rotman透镜,平面波导模型法;轮廓积分方程法
Numerical Analysis of Rotman Lens-type Multiple Beamforming Networks
YUAN Ning,LIANG Chang-hong,ZHENG Jia-jun
(Dept.of Microwave Telecommunications Engineering,Xidian University,Xi'an 710071,China)
Abstract:The analysis of Rotman lens,an important multiple beamforming network is accomplished by the contour integral equation method along with the planar waveguide model method.First,the planar waveguide models for Rotman lens and its feed lines which incorporate the dispersion effect with frequencies are set up.Then the aperture electric fields at lens ports are expanded by appropriate waveguide mode functions and substituted into the contour integral equation.The multimode scattering matrix of the lens can be acquired by solving the contour integral equation by using Galerkin method.To obtain the scattering matrix corresponding to the dominant mode,higher order modes aroused at lens ports are treated as loads of the network.It is proved that the calculated results are in good agreement with the experimental ones.
Key words:multiple beam forming network;Rotman lens;planar waveguide model method;contour integral equation method
一、引 言
Rotman透镜是一种产生多波束体制的有效手段,近年来在电子战、预警系统及个人通讯系统中得到了越来越广泛的应用.与其他多波束馈电系统相比,它具有一些显著的优点[1]:(1)由于它是基于等光程原理,因此波束的指向不随频率变化;(2)每个波束具有全口径增益;(3)常以微带形式实现,因而电路简单,体积小,重量轻;(4)具有很好的宽带性,可达倍频程带宽.
当参数给定后,Rotman透镜的输入输出轮廓可由几何光学设计公式确定[1].但对透镜性能有重要影响的虚端口轮廓不受设计方程的约束,是设计的自由度.为了对透镜参数及虚端口进行优化设计,必须对透镜边缘的场分布有所了解.本文将平面波导模型法与轮廓积分方程法相结合对Rotman透镜进行了严格的分析.由于Rotman透镜常工作在较高的频率(几GHz~十几GHz)及较宽的频带内,因此在建立其等效平板波导模型时,考虑了等效参数对频率的色散效应,从而计入了高阶模的影响,并能更精确地反映实际情况.在求得透镜及相连馈线的等效平板波导模型后,根据透镜内部场的特性,在其端口上采用适当的波导模式函数展开电场,并代入场满足的轮廓积分方程,用Galerkin法求解这些展开系数,便可得到透镜的多模式散射参数.通常,透镜端口由渐变线连接至只传输主模的馈线上,因而本文将由于端口非均匀性引起的高阶模看作网络的加载,从而得到TEM模激励的透镜的散射参数.本文方法考虑了高阶模的影响、轮廓间的多次反射效应以及各端口之间的耦合,因而能较准确地反映透镜性能,且该方法的收敛性很好,只需取前几个展开模式,因而计算量小,速度快,非常适用于电尺寸较大的Rotman透镜的数值分析.
二、等效平板波导模型的建立
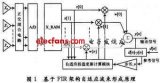
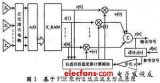
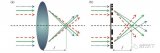
图1给出了一微带线及其等效的平板波导模型的剖面图.在图1(b)的波导模型中,上、下端为电壁,左、右端为磁壁,其中充满了介电常数为εe(f)的介质,模型的高度h等于微带介质基板的厚度.

|
图1 微带线及其等效的平板波导模型 为了使该等效模型能反映高阶模的效应,在整个频带内均适用,我们考虑了等效参数的色散效应,动态等效介电常数εe(f)和等效宽度we(f)随频率变化的关系为[2]:
其中εeff和weff分别为静态等效介电常数和等效宽度,fT是最低阶模的截止频率,定义为:
式中c为自由空间的光速,Δw代表微带边缘的边缘场效应.对于不同的宽高比w/h,Z0和εeff的表达式也不尽相同,本文采用Gupta的经验公式[3]计算Z0,εeff和Δw.静态等效宽度weff可由下式确定:
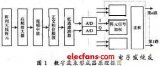
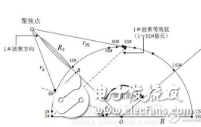
计算出fT、εeff和weff后,就可根据式(1),(2)求出不同频率时的εe(f)和we(f),由此可将微带线等效为相应的平面波导模型.对于图2所示的微带型Rotman透镜,其等效平板波导模型应为原透镜的相似形.当透镜的形状确定后,其所有端口的宽度就可以知道,利用前述方法可求出每个端口的等效宽度,再以这些等效端口宽度作为约束条件,并保持透镜的中心不变且等效轮廓的每一段均平行于原透镜的相应段,求原透镜的相似形就可得到满足以上频率色散效应的等效平板波导模型的轮廓,以下的分析均是针对此等效模型进行的. |

|
图2 Rotman透镜示意图 三、多模式散射参数及高阶模式的处理
其中H(2)0和H(2)1表示第二类零阶和一阶汉克尔函数,s和s′分别表示轮廓c上的场点和源点,r=r
因为透镜腔内只有Ez,Hx,Hy三个分量不为零,因而在与其相连的平面波导中,只有TEp0(p=0,1,2,…)模式存在,用这些正交模式函数来表示端口上的场分布(即M个模式):
式中Akp和Bkp分别表示在第k个端口处入射和反射的p阶模,Ykp和γkp分别为其模式导纳和传播常数,wk是第k个端口的宽度,εp为纽曼常数,当p=0(对应TEM模)时,εp=1,p≠0时,εp=2.采用本地坐标系统分析各端口,则由式(7)可得下式:
根据式(7)写出Ez(sm)和Ez(s′n)的展开式,与式(8)一起代入式(6)可得:
采用Galerkin法,取权函数
其中:
当m≠n即场点和源点位于不同区域时,上两式的二重积分可用数值积分法方便地求得,当m=n即场点和源点位置于同一区域时,Gmnij=0,而Fmnij出现奇异性,可用变量代换结合奇异点去除法巧妙求解[6]. CB=DA (13) 其中矩阵C和D的元素分别为: Ckl=(Ynj)-1(γnjFmnij-kdGmnij), A、B分别代表如下的列矢量: A=[A10A20…AN0 A11…AN1…A1M-1…ANM-1]T (16) 其中Akp和Bkp分别表示第k个端口第p阶模的入射波和反射波.解式(13)的矩阵方程可得Rotman透镜的多模式散射矩阵: S=C-1D (18) 通常情况下,透镜端口通过渐变线连接到只传输主模的传输线上,端口激励起的高阶模式的能量在渐变线内不断反射回透镜腔,最终只有主模传播.我们把这些凋落的高阶模看作透镜这个多端口网络的加载.第m个端口的第i阶模的特性阻抗Zm0i可用下式计算[7]:
则第m个端口的第i阶模对应的负载反射系数为: Γ(i-1)N+m=(Zm0i-Zm0)/(Zm0i+Zm0) (20) 其中Zm0为相应端口的等效平面波导的特性阻抗.设在所有N×M个端口中,主模对应的第1~N个端口为Ⅰ区,其余(M-1)×N个高阶模式对应的端口N+1~N×M为第Ⅱ区,则由主模激励,高阶模加载的透镜的单模散射矩阵[Sm]可由式(18)得到的多模式S矩阵的元素按下式求出[8]: [Sm]=[SⅡ]+[SⅠ Ⅱ]{[Γ]-1-[SⅡ Ⅱ]}-1[SⅡ Ⅰ] (21) 其中[Γ]为由高阶模式端口N+1~N×M的负载反射系数组成的对角矩阵. 四、算例与讨论 |

|
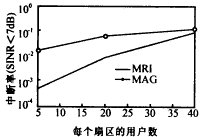
图3 计算和实验所用的32×32元Rotman透镜 图4(a)中方框线代表波束口1激励时,实验测得的输出端口的幅度分布,圆圈线为理论计算的结果,图4(b)为相应的相位分布.图5(a)和5(b)分别为中心波束口16激励时,输出端口的幅度和相位分布.由图可见,边缘端口的幅度起伏比较大,而中心端口的幅度较为平稳,而无论对于边缘端口还是中心端口,实验结果与计算结果均吻合得很好,除个别点外,幅度误差通常在0.5dB左右,相位误差一般在十度以下,证明了本文方法的正确性和有效性.本例的透镜由于焦角选择得比较合适,因而虽然输入端口较多,但相互之间的耦合很小,隔离较好,由表1给出的波束口1和16与其他波束口之间的隔离度即可看出这一点.
图4 (a)输入端口1激励时输出端口的幅度分布;(b)输入端口1激励时输出端口的相位分布 |

|
图5 (a)输入端口16激励时输出端口的幅度分布;(b)输入端口16激励时输出端口的相位分布 表1 输入端口之间的隔离度 |
| 波束口序号 | 1-2 | 1-4 | 1-8 | 1-12 | 1-16 | 1-20 | 1-24 | 1-28 | 1-32 |
| 隔离度(dB) | -17.78 | -24.89 | -26.93 | -45.81 | -24.88 | -27.26 | -31.83 | -26.08 | -29.32 |
| 波束口序号 | 16-1 | 16-4 | 16-8 | 16-12 | 16-17 | 16-20 | 16-24 | 16-28 | 16-32 |
| 隔离度(dB) | -25.73 | -26.54 | -27.45 | -23.5 | -13.01 | -24.21 | -28.82 | -26.1 | -31.14 |
| 五、结 论 本文首先建立了Rotman透镜的含色散效应的平面波导模型,然后利用波导模式函数展开待求电场,结合轮廓积分方程法完成了对Rotman透镜性能的分析.由于方法的收敛性较好,只需取前几个展开模式,因而本文方法较边界元法计算量小,计算速度快,且由于考虑了高次模的影响,从而更能反映实际情况,计算所得结果与实验吻合得很好.利用本文方法可方便地考察透镜各参数及虚端口轮廓对其性能的影响,实现透镜轮廓的优化设计. |
 电子发烧友App
电子发烧友App






 (6)
(6) (8)
(8) (9)
(9) (10)
(10) (12)
(12)
















评论