故障特征提取的方法研究

摘要：针对常规特征提取方法存在着问题不足，提出了基于BP神经网络和基于互信息熵的特征提取方法，并通过特征提取实例加以说明。结果表明这两种方法是可行和有效的。

随着科学技术的发展，现代设备的结构日趋复杂，其故障类型越来越多，反映故障的状态、特征也相应增加。在实际故障诊断过程中，为了使诊断准确可靠，总要采集尽可能多的样本，以获得足够的故障信息。但样本太多，会占用大量的存储空间和计算时间，太多的特征输入也会引起训练过程耗时费工，甚至妨碍训练网络的收敛，最终影响分类精度。因此要从样本中提取对诊断故障贡献大的有用信息。这一工作就是特征提取。

特征提取就是利用已有特征参数构造一个较低维数的特征空间，将原始特征中蕴含的有用信息映射到少数几个特征上，忽略多余的不相干信息。从数学意义上讲，就是对一个n维向量X＝[x1，x2，…，xn]T进行降维，变换为低维向量Y＝[y1，y2，…，ym]T，m

特征提取的方法有很多，常用的方法主要有欧式距离法、概率距离法、统计直方图法、散度准则法等。本文针对现有方法的局限性，研究基于BP神经网络的特征提取方法和基于互信息熵的特征提取方法。

1 基于BP神经网络的特征提取方法

要从N个特征中挑选出对诊断贡献较大的n个特征参数(n

εij=|(аYi)/(аXj)|

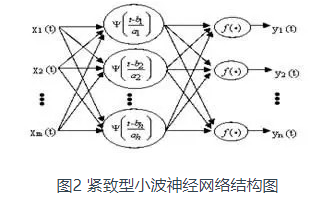
采用三层BP网络，输入层n个单元对应n个特征参数，输出层m个单元对应m种模式分类，取中间隐层单元数为q，用W B iq表示输入层单元i与隐层单元q之间的连接权；用w O qj表示隐层单元q与输出层单元j之间的连接权，则隐层第q单元的输出Oq，为：

输出层第j个单元输出yj为：

式中j=1，2，…，m；εj为阈值。

则特征参数xi对模式类别yj的灵敏度为：

代入（1）式，则特征参数Xi的灵敏度εij和特征参数Xk的灵敏度εkj之差可整理为：

大量的试验和研究表明，当网络收敛后有：a1≈a2≈…≈aq。

从上式可以看出，如果：

则必有：εij＞εki

即特征参数Xi对第j类故障的分类能力比特征参数Xk强。

将特征参数X和分类模式分类结果y组成的样本集作为BP网络的学习样本，对网络进行训练。设Wiq和Wkq分别为与特征参数Xi和Xk对应输入单元与隐层单元q之间的连接权系数，记：

│Wεi│=│Wi1│+|Wi2|+…+|Wiq|

│Wεk│=│Wk1│+|Wk2|+…+|Wkq|

如果│Wεi│>│Wεk│，则可以认为Xi的特征灵敏度εi比特征参数Xk的灵敏度εk大。这样可知特征参数Xi的分类能力比特征参数Xk的分类能力强。

2 基于互信息熵的特征提取方法

由信息特征可知，当某特征获得最大互信息熵，该特征就可获得最大识别熵增量和最小误识别概率，因而具有最优特性。特征提取过程就是在由给定的n个特征集X二{XI~X2，…，zn)所构成的初始特征集合情况下，寻找一个具有最大互信息熵的集合：X＝{X1，X2，…，Xk}，k

在一定的初始特征集合下，识别样本的后验熵是一定的。在实现特征优化过程中，随着特征的删除，会有信息的损失，使得后验熵趋于增加。因此后验熵增值大小反应了删除特征向量引起的信息损失的情况。当删除不同特征及删除特征数逐步递增时，会对应有不同的后验熵。按后验熵由小到大排列，可获得对应的特征删除序列。其过程可描述为：

(1)初始化：设原始特征集合F＝{N个特征}，令初始优化特征集合S＝[K个特征，K=N]；

(2)计算后验熵；

(3)实现递减：S＝[K-1个特征]，并计算相应的后验熵；

(4)选择优化特征集合：以多个递减特征集合所对应的后验熵为依据，选择具有最小后验熵增的特征向量集合为优化特征集合S[N-1个优化特征]；

(5)返回(3)，重新计算，直到满足分类要求，选择具有最小后验熵的优化特征集合；

(6)输出优化特征集合。

3 特征提取实例

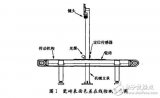
在热电厂的发电机组工作中，发电机组主轴经常遇到如喘振、流体激励等故障。这些故障不仅会引起生产效率下降，而且会对机器造成严重危害，影响机组的安全运行。传统的诊断方法是在主轴轴承处加传感器进行振动测试，得到其频谱图；然后在频域内分析，根据基于能量分布的故障诊断理论将振动信号功率谱密度按一定的规则进行量化，利用神经网络等工具进行故障诊断。但是喘振、流体激励等故障在频域内通常表现为连续分布的有色噪声带，在频域内分析难以区分，难以进行频谱特征提取，全息谱分析方法也不甚有效。传统方法增加了系统的开销，诊断效果不理想。如果在时域内采用信息优化方法做预处理，再用传统的诊断方法进行诊断，可以收到很好的效果。

本文采用时域内故障振动信号的方差、峭度、偏斜度等参数，分别利用BP神经网络和后验熵分析对其进行特征提取，研究如何从中找出最能反映故障的特征。

表1为主轴喘振、流体激励故障时振动信号在垂直和水平方向的方差、峭度、偏斜度等6个参数的数据。

表1 主轴故障的特征参数

 

序号	喘振						流体激励
	均方差		峭度		偏斜度		均方差		峭度		偏斜度
	垂直	水平	垂直	水平	垂直	水平	垂直	水平	垂直	水平	垂直	水平
1	7.50	9.21	-0.02	-0.00	-0.22	-0.10	40.2	44.1	0.22	-0.42	-0.11	-0.08
2	26.1	15.2	-0.75	-0.92	-0.31	-0.21	70.1	20.5	3.82	1.78	0.00	0.16
3	13.8	9.21	-0.81	-0.72	-0.29	0.19	12.4	14.2	-0.38	-0.62	0.03	0.01
4	6.2	8.5	-0.01	-0.04	-0.22	-0.23	8.15	33.5	0.15	-0.14	0.07	0.10
5	36.1	11.2	-0.61	-0.01	-0.23	0.07	7.21	15.2	-0.41	-0.51	0.01	0.01
6	11.5	9.71	-0.81	-0.93	-0.31	-0.18	25.7	30.2	-0.37	0.19	-0.11	-0.06
7	33.1	28.2	-0.79	-0.85	-0.07	-0.45	71.2	25.3	3.81	1.85	0.01	0.16
8	37.2	26.8	-0.81	-0.87	-0.06	-0.41	8.11	35.2	-0.81	-0.13	0.01	0.11

 

设原始特征集合F＝{x1，x2，x3，x4，x5，x6}，其中x1、x2分别为垂直、水平方向的均方差，x3、x4分别为垂直和水平方向的峭度，x5、x6，分别为垂直和水平方向的偏斜度。

① 基于BP神经网络的特征提取方法：采用表1中的数据作为BP神经网络的输入，编制程序对神经网络进行训练，训练算法采用标准BP算法和Levenberg-Mar-quardt法两种方法来训练BP网络，从而计算特征参数的特征灵敏度，确定出对结果影响最大的特征参数。

喘振：

│W1│={1.5874 1.6553 25.5320 25.1765 74.4724 40.4295}

流体激励：

│W2│={1.5874 1.6553 25.5320 25.1765 74.4724 40.4295}

从结果可以看出：偏斜度对这两种故障最为敏感，反映了低频自激故障的主要特征。

② 基于互信息熵的特征提取方法：原始特征集合F＝{x1，x2，x3，x4，x5，x6}对应表1中的特征参数。在特征参数优化过程中，随着特征的删除，后验熵变化较大。当删除的特征中包含有x5、x6时，后验熵明显降低；如仅保留x5、x6时，后验熵最小。说明偏斜度对这两种故障最为敏感。

对比这两种特征提取方法，可以看出它们得到的结论是一样的。如果采用通频全息谱法来进行分析，得到的结论相同，从而验证了这两种特征提取方法的有效性。

在实际的状态监测和故障诊断中，可以重点监测系统的偏斜度，配合对振动信号的频谱分析，可以快速地判断故障类型和具体发生的时间。