这是达林顿(S. Darlington)经典著作,现代网络综合的开山之作,滤波器类文章引用最高文章,他总结了之前滤波器的设计方法,并指出其缺陷,首次提出了使用插入损耗来设计滤波器的方法,这种方法一直沿用至今。将这篇文章分四次发表,这是其二。
综合特定插入损耗指标的LC四端口网络(二)
SYNTHESIS OF REACTANCE 4-POLES WHICH PRODUCE PRESCRIBED INSERTION LOSS CHARACTERISTICS
包括对滤波器设计的特殊应用
作者 S. Darlington*
使用实际电路结构实现开路和短路阻抗
已经开发出了设计方法,用于设计产生规定的开路和短路阻抗的各种不同的LC四端口网络电路结构,例如通过第一部分中描述的方法从插入损耗函数确定的阻抗。据说其中一些电路结构是规范的(Canonical),因为它们可以被设计为具有任何一组可以用物理LC网络实现的阻抗。其他的则不那么通用,但可以更有利地使用,或者是通用电路结构的特殊情况,已经为其开发了更简单的设计方法。
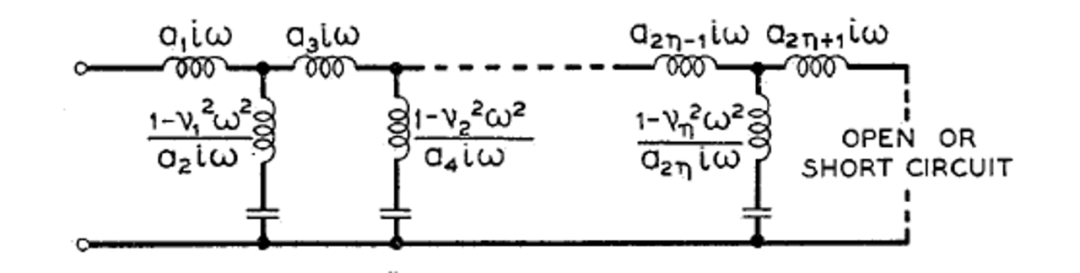
Cauer规范电路结构
最简单的一般设计理论适用于由Cauer (5)引入的两种规范LC 四端口网络的设计。它们的电路结构如图6所示。它们是根据三个开路阻抗或短路导纳的部分分式展开设计的,通过注意不同展开的部分分式之间的某些关系以及这些部分分式与各网络分支的对应关系来设计。由于Cauer已经非常完整地描述了这些网络,因此在这里没有必要更详细地描述它们。
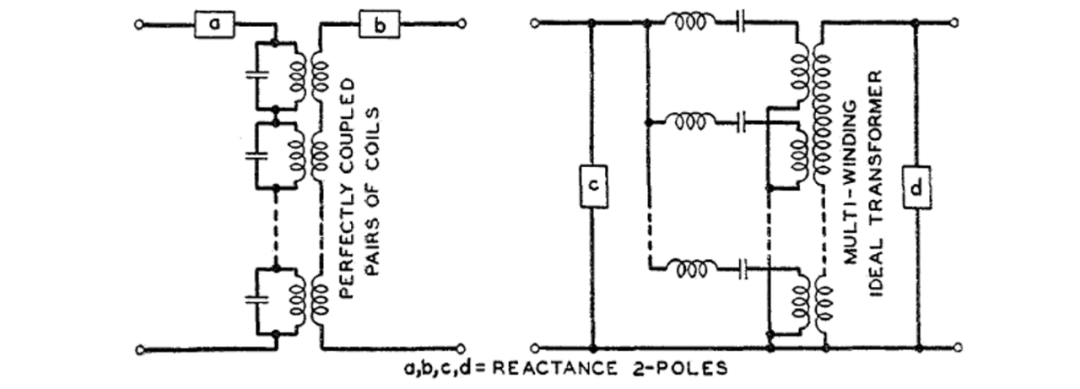
图6 Cauer的规范LC 四端口网络
规范的串联段电路结构
Cauer的规范电路结构仅在LC四端口特性的理论研究中特别有趣。当涉及到实际应用时,几乎总是更喜欢使用由简单网络或段以图7所示的串联方式连接而成的等效电路。在选择性网络或滤波器的情况下,使用串联段通常是实际的需要。首先,使用串联段允许通过不那么精确地调整元件到其理论值来获得对理论传输特性的合理近似。
此外,最常见的滤波器可以以串联形式构建,而无需使用Cauer规范电路结构的等效网络所需的互感。

图7 串联四端口网络电路
对于许多用途而言,梯形网络是串联组合的最有用形式。然而,即使在最一般的定义下,即任何由交替的串联和并联两端阻抗组成的序列,梯形电路结构也不能用于实现所有可用更一般的电抗四端网络实现的开路和短路阻抗。另一方面,可以表明,梯形电路结构的稍微修改或推广总是可以实现的,因此可以被称为规范电抗四端网络。该电路结构定义为四种类型的任意串联组合,如图8所示,可能在网络的一端和理想变压器串联。
在许多情况下,上述规范网络中并不需要所有四种类型的段,而且经常出现没有理想变压器的情况。事实也证明,串联电感通常可以包含在串联分支中或类型的网络中,这样可以使类型和中的感性耦合不那么理想,甚至可以被这些部分中的并联自感完全替代。例如,在大多数滤波器中,既没有类型的段也没有理想变压器,而类型中的感性耦合几乎总是可以消除的。
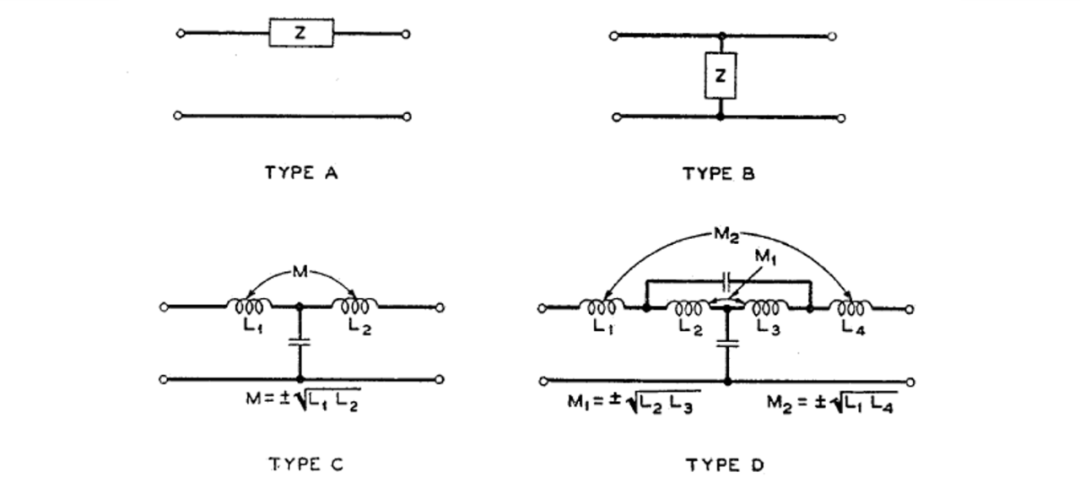
通用的LC二端网络。类型和可能是不对称的。
图8 产生规范LC四端网络的串联段类型
串联段电路结构的一般理论
一端以恒定电阻终端的LC四端口网络的输入阻抗可以很容易地从开路和短路阻抗中确定。相反,可以证明,除了对应于交换输入或输出端子的可能性的传递阻抗的符号有明显的模糊性之外,开路和短路阻抗通常可以从对应于规定的终端电阻的阻抗函数中确定。该规则的唯一例外对应于导致降低阶数的阻抗的终端值,并且对于任何一个网络,这样的值只能是有限的。
根据上述原则,获得规定的开路和短路电抗阻抗的一种方法是,将一个以电阻终端的LC四端口设计为一个二端口,该二端口产生的输入阻抗由开路和短路阻抗计算得出。在四端口的终端添加适当的理想变压器,将产生规定的开路和短路阻抗,前提是设计使得输入阻抗的阶数对于规定的阻抗和最终电路结构是正常的。为了从所需的开路和短路阻抗计算输入阻抗中获得假定的终端电阻,添加的理想变压器通常是必要的。
Brune(8)已经展示了如何将任何给定的正实函数实现为A、B和C类型段的串联组合的输入阻抗,前提是允许在各段之间包含串联电阻。当正实函数的电阻段的根仅以相同的对出现并且都是实数或虚数时,可以以一种方式来执行Brune的设计方法,以消除除形成终端的电阻之外的所有电阻。如果Brune的方法被最近的修改所替代,允许使用D类型的段,则对实数或虚数根的要求变得不必要。所获得的电路结构可以显示为,具有与规定函数相同阶数的阻抗函数将通过终端电阻的一般值获得,即规定函数不代表降低阶数的特殊情况。因此,可以容易地找到与任何可以产生输入阻抗的LC四端口网络相对应的串联段等效物,该输入阻抗对于电路结构是正常的阶数,并且电阻部分的所有根都以相同的对出现。这被证明是所有物理LC四端口网络的特性。
上述分析证明了通过在A、B、C、D类型的串联组合的一端添加一个理想变压器而形成的LC四端口网络的规范性质。还可以证明,通过一对端子通过电阻终端闭合而形成的两端阻抗构成一个规范的一般二端口。如上所述,这种类型的二端口可以对应于任何正实函数,前提是电阻部分的根仅以相同的对出现。然而,当允许使用导致降低阶数的阻抗函数的终端电阻的特殊值时,对正实函数的限制变得不必要。由于LC四端口网络的规范性质,这可以通过仅仅展示如何找到一组导致由任何给定的正实函数表示的输入阻抗的物理开路和短路电抗阻抗来证明。如何完成这一点如下所示。
假设要设计一个LC网络,以便在远端以规定的电阻终端时在一端产生规定的输入阻抗。由于输入功率和接收功率的相等性,可以通过规定的阻抗容易地计算出在第二个电阻终端输入端时将获得的插入损耗。然后可以使用第一部分的通用理论来确定相应的物理上可实现的开路和短路阻抗集。很容易证明,如果它是一个正实函数,那么其中一个将对应于规定的阻抗。
设计流程
现在考虑设计串联LC四端口网络的实际操作,该LC网络产生规定的开路和短路阻抗。如上所述,第一步是计算网络任意一端的输入阻抗,该端对应于任意的远端终端,但要求阻抗函数的阶数必须对开路和短路阻抗正常。然后设计一种类型为或的段,使其在被较低次的新物理阻抗终端时产生所需的输入阻抗。接着设计第二段,使其在被进一步降低阶数的新阻抗终端时产生所需的终端阻抗。这一过程一直持续到所需的终端阻抗降低为恒定电阻为止。最后,用理想变压器与电阻的等效组合代替所需的终端电阻,该电阻与计算原始输入阻抗时假定的终端电阻相同。
Brune展示了如何将具有实频轴上极点或根的任何正实函数分别实现为类型为或的段的输入阻抗,并在降低阶数的阻抗下被端接。Brune还展示了如何将没有实频轴上的根或极点,但电阻部分有一对相同的实根或虚根的正实函数实现为类型的段在被降低阶数的物理阻抗下的输入阻抗。最后,如果输入阻抗的电阻部分的所有根都以相同对出现,则每种情况下所需的终端阻抗都具有相同的特性。因此,为了完成设计方法的解释,只需要展示电阻部分的相同复根的出现如何允许使用类型为的段,就像当根是实数或虚数时使用类型为的段一样。
D型段的设计
假设某一规定的D型段在阻抗端接时产生规定的输入阻抗。如果用表示D型段的行列式,并将输入和输出网格分别编号为1和2,则与的关系为:
其中,表示D型段在终端的短路阻抗。假设是一个正实函数,其电阻部分具有一对相同的复根,可以证明以下条件始终确定一个物理上的D型段,该线段导致一个比更低阶数的物理上的:函数和需要具有一对重复根,它们也与的电阻部分的一对复根重合。
可以轻易证明,上述的和的根的重合会导致阻抗中不是的根的所有根都被抵消,这就排除了在平面的右半部分存在根的可能性。如果还假设D型段是物理上可实现的,简单的附加分析表明必须实际上是一个正实函数。这证明了本身的正实性,但不排除在中,的重合极点的正留数掩盖了具有负留数的实极点。最后,可以证明,通过向原始输入阻抗添加,可以在不改变的相应留数的情况下分离两个阻抗的任何重合极点。可以通过证明上述条件导致表达式的根和极点的八次重合来证明的阶数降低。
为了证明和的根的条件实际上导致了一个物理上的D型段,首先从该条件推导出元件值的显式公式,而不考虑物理可实现性的问题。输入阻抗在这些公式中仅通过及其电阻部分的双重根处的导数值出现。这允许在公式中用产生输入阻抗并在适当的恒定电阻下端接的物理LC四端口的开路阻抗替换。然后可以证明,D型段的相应电容和自感将是有限的正实数。
梯形网络所需的条件
当所有插损无限大的频率都是实数或虚数时,D型段不必包含在规范串联段电路中。这是因为完整网络的无限损耗频率是各个部分的相应临界频率,而D型段仅需要实现无限损耗的复频率。当D型段不存在时,网络可以被视为一般的电抗梯形网络,这可以定义为由LC两端口组成的交替串联和并联支路的任意组合。虽然C型段中的串联电感之间的耦合使它们比交替串联和并联两端口更复杂,但可以将耦合视为仅仅是实现等效网络中出现的负电感的装置。
中间串联低通梯形电路结构
在上述类型的梯形网络中可能存在的大量组合,只有少数是常用的。为了确定元件值而不涉及使用前面描述的串联段的一般理论所需的工作,已经为这些特定电路结构开发了广泛的特殊设计理论。特殊设计理论最好首先针对图9所示的特定类型的梯形进行开发,尽管它不一定是镜像参数理论中的中间串联型低通滤波器,但也可以被称为中间串联低通电路结构。其他常见的电路结构可以通过对这个特例的理论进行简单的修改来设计。
最早计算图9所示的中间串联低通结构的梯形元件值的特殊公式是由Norton(7)作为他的恒阻对滤波器理论的一部分而开发的。尽管Norton的公式代表了中间串联低通梯形理论发展的重要一步,但已经发现在数值问题中它们所要求的计算过于复杂,通常必须进行非常高精度的数值计算。
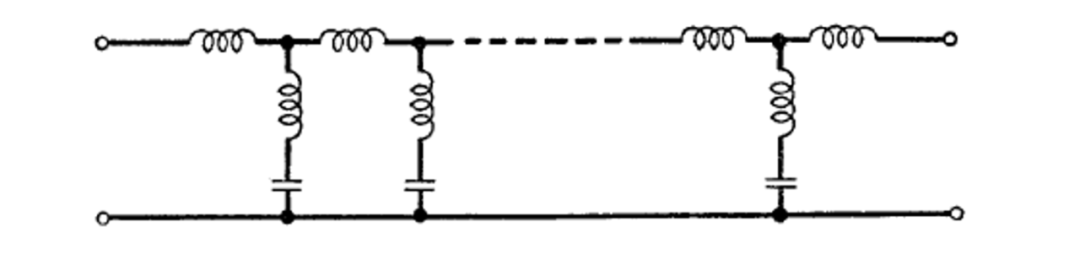
图9 中间串联低通梯形电路结构
因此,对设计问题进行了广泛的进一步分析,推导出了一组新的公式。这些新公式在数值计算方面相对令人满意,并且在各种理论研究中也很有用,例如确定可以用中间串联低通梯形实现的阻抗。此外,公式的推导涉及另一组公式的开发,这组公式以非常紧凑的形式用行列式表示,并且在某些理论研究中很有用,尽管当应用于普通数值问题时它们具有与Norton公式相同的缺点。
推导设计公式的假设和条件
如果暂时采用某些简单的假设,中间串联低通电路结构的梯形设计公式的发展会得到简化。当这些假设不满足时,应遵循的方法最好在公式推导出来之后进行研究。首先,最简单的方法是从假设一组开路和短路阻抗开始,这些阻抗预先知道适合该电路结构,将具有这种特性的阻抗问题留到以后解决。尽管可以找到需要排除某些解的特殊阻抗集,但进一步假设阻抗是这样的,通常遇到的元件解的多重性都是可能的。尽管在某些特殊情况下,某些开路和短路阻抗的阶数可能会降低,但暂时假设所有插损无限大的频率都是不同的,并且所有开路和短路阻抗对于该电路结构都是正常阶数,也可以避免某些困难。
以下关系适用于与上述假设一致的任何中间串联低通电路结构的梯形网络,是所有已知元件值公式的基础。首先,并联支路的谐振与插损无限大的频率相同,除了在无穷大处的一个无限损耗点。其次,在并联支路谐振时,任何开路和短路驱动点阻抗的假设值独立于与其终端被并联支路隔开的元件,该并联支路在梯形中起短路作用。最后,在假设电路结构的正常阶数阻抗下,驱动点阻抗函数相对于频率的导数具有相同的特性。
事实证明,上述关系足以从一个开路或短路驱动点阻抗以及插损无限大的频率来确定所有元件值,除了开路阻抗情况下的远端电感。通常可获得的解的多重性只是由于无限损耗的有限频率可以任意分布在并联支路作为其各自的谐振。为了获得唯一的解,最好一开始就假设已经选择了特定的分布。然后问题就变成了将一个已知的LC二端阻抗实现为中间串联低通电路结构的梯形的开路或短路阻抗,其并联支路谐振已经规定。
连分数展开基础
元件值公式的开发需要引入广泛的特殊符号,以便将设计问题简化为确定已知函数的特别简单的连分数展开。首先,考虑图10所示的各网络支路阻抗的指定中的常数,用而不是表示,这样更简单。 常数代表以表示的并联支路谐振或无限损耗有限点的倒数,因此假定它们是已知的。因此,所考虑的问题相当于确定所谓的梯形网络系数,因为从这些系数和一起确定元件值没有任何困难。为了避免前面提到的设计公式的歧义,这些公式仅仅是各个的特定公式,方便地包含附加要求,即系数等的编号应从它们要计算的特定开路或短路驱动点阻抗的端子开始。
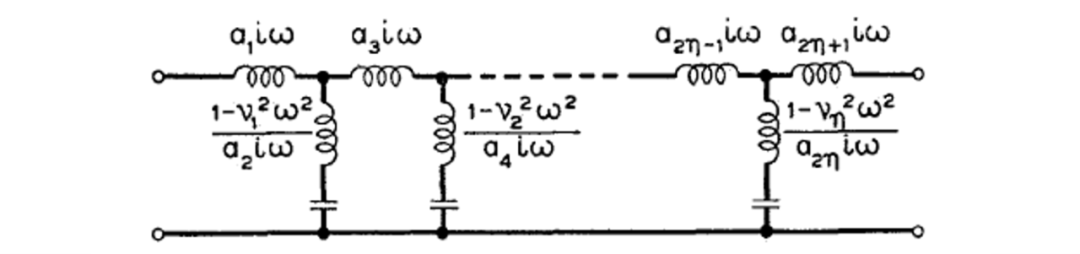
图10 中间串联低通梯形的阻抗支路设计
众所周知,将2端阻抗实现为规定电路结构的梯形网络的输入阻抗的问题相当于获得阻抗的某种规定形式的连分数展开或一些相关函数的问题。对于所考虑的特定网络,如果要展开的函数是通过将阻抗函数除以或其等效的而得到的,则所需的连分数是最简单的。换句话说,最好定义为
其中是计算系数等的开路或短路阻抗。
由于是的奇有理函数,因此必须是的函数。这建议用新变量替换以降低的次数。然而,事实证明,如果使用此变量的倒数,则会获得更简单的连分数。因此,引入了以下附加符号:
其中表示新变量,而表示对应于无限损耗频率的的值。用这种符号表示,所需的连分数展开具有以下形式:
问题是解决这个恒等式的,假设常数和变量的函数是已知的。
在推导通过上述问题的解决而开发的更有用的公式时,分析的第一部分致力于推导前面提到的以行列式形式紧凑表示的替代公式。最终的公式然后通过将行列式展开为函数的部分分式表示来推导。由于推导的两个部分都涉及漫长而复杂的代数运算,因此在这里只对其进行简要概述。如果行列式中初步公式的陈述先于它们推导的概述,将更加明晰。
以行列式表示的的公式
在的初步解中出现的行列式由形成,定义为上述符号表示的:
其中, 等用于表示和在等处的取值。使用符号和是一致的,因为是当接近时所接近的极限。
行列式本身有三种不同的类型。行列式定义为,其中和取值从1到。即,
行列式是通过将的最后一列的元件更改为1而获得的。即,
最后,行列式是通过将的最后一列的元件从更改为而获得的。因此,
除了之外,所有这些行列式都给出了梯形网络系数的公式。这些系数由以下设计方程给出:
系数对应于形成最后一个串联支路的电感。如果函数是从开路阻抗获得的,则必须从其他阻抗确定该系数。如果对应于短路阻抗,则可以从在零频率下的值或通过使用上述公式和任意附加常数来找到。
上述公式可以通过一种相当直接但冗长且繁琐的归纳法推导出来。首先从Norton方程或直接从连分数(25)在和附近的行为推导出前四个系数的公式。这给出了上述的关于和的特殊公式,并显示了关于和的公式与关于和的一般公式一致。然后证明如果关于和的公式是正确的,那么关于和的公式也必须是正确的。这首先通过使用关于和的公式来表示从网络中移除前两个分支(对应于和)所得到的“简化”阻抗中的和来完成。然后将这个“简化”阻抗替换为原始阻抗和关于和的公式的等效表达式。最终通过对结果方程中行列式的大量操作得出关于和的一般公式。
除非所有的常数都是不同的(符合最初的假设,即没有两个相同的无限损耗频率),否则公式(30)是不确定的。然而,可以通过假设无限小的差异并使用Taylor级数展开表示作为 的函数来处理重合的无限损耗频率。当所有的无限损耗频率都是相同的,除了一个在无穷大处的频率时,连分数(25)变成一个由Fry(12)考虑的Stieltjes分数类型。无疑可以通过Taylor级数方法从(30)推导出Stieltjes分数展开中的已知常数公式。
在得出最终公式后,通过展示如何扩展第一组行列式,最好考虑除了没有两个相同频率的无限损耗之外的摒弃原始假设的效果。
通过展开行列式推导最终设计公式
可以轻易证明,如果将函数展开为部分分数的和,只要从中推导出的开路或短路驱动点阻抗在物理上是可实现的,该展开将始终采用以下形式:
在这个表达式中,除了有时可能为零之外,所有的和都是正的且都是有限的。
根据的部分分数展开,如(26)中定义的行列式元件变为:
而只需在此公式中将等于即可得到。出现在的公式(30)中的由(27)至(29)定义的行列式可以根据这些的部分分数表示进行展开。然而,这些展开的推导过程太长且复杂,只能在此简要概述。
在推导行列式的展开时,首先检查与展开中的部分分数数量相同的特定行列式。发现这个特定的行列式可以表示为两个一般形式为的行列式的乘积,这在行列式理论的著名论文中进行了评估。然后证明了较高阶的行列式必须为零,而较低阶的行列式则等同于可分解的相似行列式的和。这些和中的每一项实际上都是通过仅使用的部分分数中的个来获得的行列式,即,通过将(32)中除了个之外的所有设置为零。对于每个可能的个部分分数的选择,必须有一个这样的项。确定了行列式的展开之后,可以通过将它们视为行列式的某些极限情况来展开和行列式。
当将这些行列式的展开插入到用于计算的方程(30)中时,可以消去无穷大损耗点等之间的差的各种因子。然后,这些公式变为:
其中,代表原始行列式展开的未取消部分。
这些最好用这些量来表示,这些量由递归公式定义:
用这些量来表示,在一般情况下需要非常复杂的求和和乘积符号。因此,最好通过列出足够多的特定情况来避免一般情况的必要性,以确定这样的声明必须显示什么。
简化后的的公式列在表I中,以及在实际计算梯形网络系数时所需的额外先前关系。这些足以表示一般情况,并且对于普通的设计目的也足够了,特别是当网络的两端的阻抗已知时,可以从每端确定部分元件。然而,通过为特定段数开发更专门形式的方程,可以获得一些额外的简化。阻抗在零和无穷大的行为也可以有利地用于确定一个或两个系数,对于这些系数,标准公式最复杂或用于检查目的。还推导出了对称格型网络的梯形等价的特殊简化公式,这些公式通常在对称电路的设计中首先计算。然而,当考虑格型网络的理论时,最好在后面介绍这些公式。
在普通的数值问题中,展开的公式不需要极高的计算精度,而在使用Norton方程或行列式公式时通常需要这种精度。同样,当遇到无限损耗的重合频率时,展开的公式不会像其他公式那样变得不确定。尽管从一个问题到另一个问题,这种情况的阶数可能会有很大差异,但这些公式也会导致普通设计问题中更直接的数值计算。虽然公式的复杂性随着网络复杂性的增加而迅速增加,使它们不适合设计超过四段或可能五段的梯形网络,但很少遇到这样复杂的网络。最后,一般段数的梯形公式假设一种形式,使它们在研究低通梯形网络的阻抗要求或避免耦合线圈等的可能性等一般研究中很有用。
表I:一般中间串联低通梯形网络
以及其它乘积和的和。
插入损耗函数与可通过中间串联低通梯形结构实现的阻抗
中间串联低通梯形结构适合实现如下形式的插入功率比:
其中,表示梯形中的并联分支数量,而和为任意常数。除了对应于和的离散选择的某些特殊情况外,总是可以通过直接的方法找到可与中间串联低通梯形结构实现并受电路结构的正常阶数和元件值的正常多重性先前假设限制的相应开路和短路阻抗。
确定阻抗的第一步是使用的分子和分母作为多项式和,为第一部分的一般阻抗理论中的多项式和找到解。很容易证明,部分中指示的多项式的解的多重性是这样的:就一般可实现性而言,和的符号可以任意选择,也可以选择的符号。除了上面提到的非常特殊的情况外,如果和的符号按照以下条件选择,则第一部分中方程(18)中展示的阻抗公式会产生与所需类型的梯形相对应的可实现阻抗:在零频率下必须为正,在无限频率下必须为负,而在零频率下必须为正或为负,这取决于终端是大于还是小于。
特殊情况下遇到的困难
在特殊情况下可能遇到的困难分为两种类型。第一种类型,尽管阻抗函数具有该电路结构的正常形式,但仍可能遇到。第二种类型对应于由于相应通用公式的分子和分母的根重合而出现的各种开路或短路阻抗,其阶数较低。
可以证明,如果所有的阻抗都是正常阶数,则无穷损耗的有限频率不能与开路或短路驱动点阻抗的根或极点重合。因此,表I的设计公式中出现的量的对应值都将是有限的。在这些量中,总是正的,但和可能是负的。因此,由表I中指示的方式由形成的量都将是有限的,但量和可能为零。的消失仅仅是用一个简单导体代替了一个串联电感,但的消失导致了对三个网络分支的要求,这些分支在所有频率上都具有无穷阻抗,一个并联分支和两个相邻的串联分支。
如果不再假定所有的的解的多样性都是物理的,则通常可以通过修改特定无穷损耗频率的选择来克服这种类型的困难,这些特定频率应作为各个并联分支的谐振,或者选择对应于相同插入损耗的不同阻抗集。然而,有可能遇到所有解决方案都导致相同困难的情况。然后必须修改梯形电路,至少使用一个反谐振电路作为串联分支。这可以通过适当地修改正常的设计方法来实现。
当存在与开路或短路驱动点阻抗的根或极点重合的无穷损耗的有限频率时,一些阻抗函数的阶数将降低。然后,通常可以通过将终端串联或并联分支或两者都添加到具有正常电路结构阻抗的中间串联损耗通梯形电路来实现阻抗。然而,通常也可能仅仅通过使用在计算元件值时仍具有正常阶数的阻抗来获得正常中间串联低通形式的完整网络。当所有阻抗都降低阶数时,可以使用正常设计方法的修改,或者使用适用于规范串联段电路结构的一般方法。
消除各种元件
允许任何或所有无穷损耗的频率置于无穷大处没有任何困难。这仅仅要求相应的并联分支是简单的电容而不是谐振电路。通过在(35)中将适当的设置为零,以及在表I的设计公式中将代表它们平方的相应设置为零来进行设计。
式(35)的一般形式中的某些功率比也导致一个或多个串联电感的消失。这类情况中有一个特殊情况特别重要,在这种情况下,一个终端串联分支消失,而下一个并联分支是一个简单的电容,留下图11所示的网络类型。功率比的适当形式是通过将分子中的项减少一个,并将的数量也减少一个从(35)中获得的。换句话说,
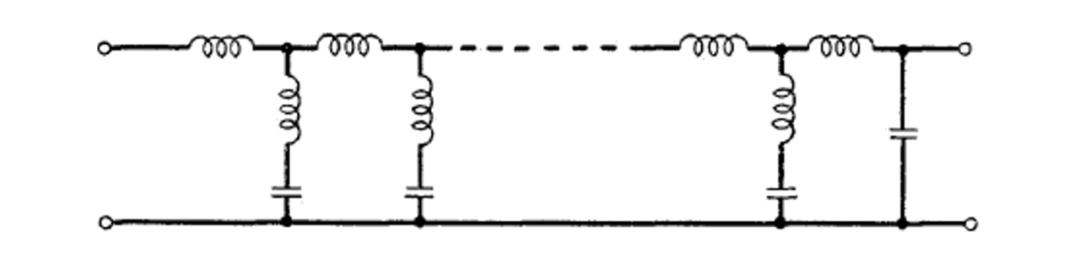
图11 与插入损耗函数的特殊形式相对应的中间串联低通梯形电路结构的特殊形式
其他常见类型的梯形网络
图12所示的梯形网络电路结构可描述为中间并联低通电路结构,通过重新定义系数(与图中所示的分支阻抗相对应)可以非常容易地进行设计。这些系数与短路和开路导纳的关系与中间串联类型梯形的系数与开路和短路阻抗的关系完全相同。因此,当中间串联和中间并联梯形网络在和端接时,只要它们的系数满足以下方程关系,就会产生相同的插入损耗:
其中,和分别是中间串联和中间并联梯形网络的系数,必须在两个网络中从相反的两端进行编号。
在中间串联类型梯形网络中可实现的负电感在相应的并联类型电路结构中变为负电容。然而,可以通过以适当的方式引入理想变压器来实现这些电路结构。要了解如何实现这一点,只需注意,由任何二端元件(如电容)并联的理想变压器等效于一对“完全耦合阻抗”,与完全耦合电感类似。
其他类型的梯形网络可以通过使用众所周知的频率变换方法来设计。先前的设计公式适用于确定一个由电抗元件组成的低通梯形网络,该网络产生的插入损耗由的适当函数表示。假设通过将替换为相关变量,将其他一些插入损耗函数变换为相同的函数。由于低通滤波器理论中的电抗元件仅仅是用于产生与或其倒数成比例的阻抗的装置,因此现在可以使用相同的理论来设计一个由与或其倒数成比例的阻抗组成的相应梯形网络。如果原始低通梯形网络的所有元件都是正数,则变换后的梯形网络的阻抗分支可以用物理两端元件实现,条件是代表物理阻抗函数。如果原始低通梯形网络包括可通过耦合线圈实现的负电感,则变换后的梯形网络中的负元件可以通过使用理想变压器来实现,就像包括负电容的中间并联低通梯形网络一样。
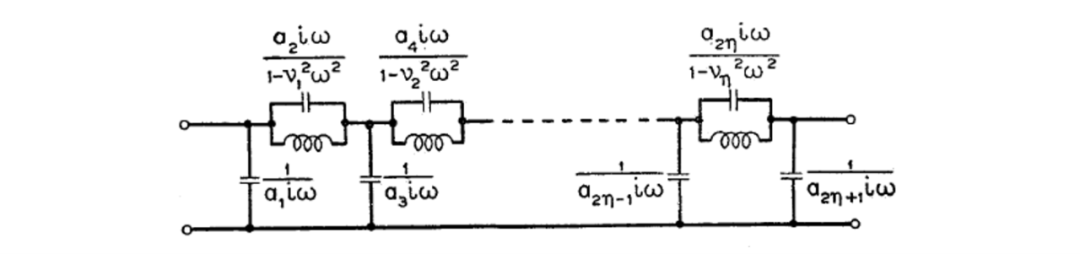
图12 中间并联低通梯形网络电路结构
通过在低通梯形网络中用电容替换电感或反之,可以获得中间串联和中间并联高通电路结构。这些电路结构可以通过定义为并使用由的函数表示的功率比来设计,这些函数与适用于低通电路结构的函数相同。带通电路结构可以通过定义为来设计,前提是当它们的插入损耗特性相对于绘制时,它们关于对称。然后,它们可以作为所有谐振在的串联和并联谐振电路的组合来实现。带阻电路结构的情况与此完全类似,其为。
通常遇到的其他梯形电路结构只有图13所示的更一般的带通类型及其逆类型。所示的串联类型通常可以设计为一个等效的更简单的网络结构,如图14所示。它可以通过图15A所示的所谓的阻抗变换从等效网络中确定。等效网络本身的形式是这样的,表I的公式可以直接应用于其设计。例如,在远离变压器的端子处测量的短路驱动点阻抗是由一个与确定中间串联低通梯形网络的开路阻抗完全相同的电路结构确定的,该梯形的远端端子并联分支由一个简单的电容组成。表I的公式没有涵盖的唯一操作是变压器阻抗比的确定,它由开路和短路驱动点阻抗在零频率时的行为来确定。
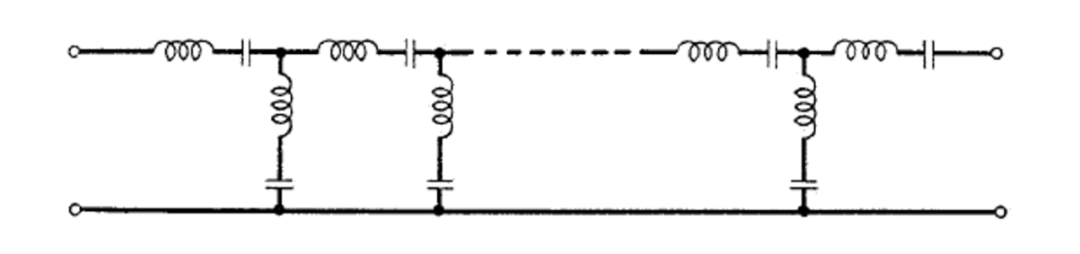
图13 一般的中间串联带通梯形网络电路结构
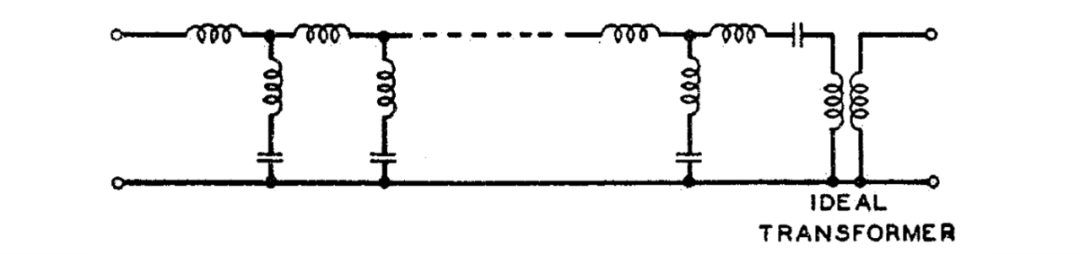
图14 图13网络的等效电路
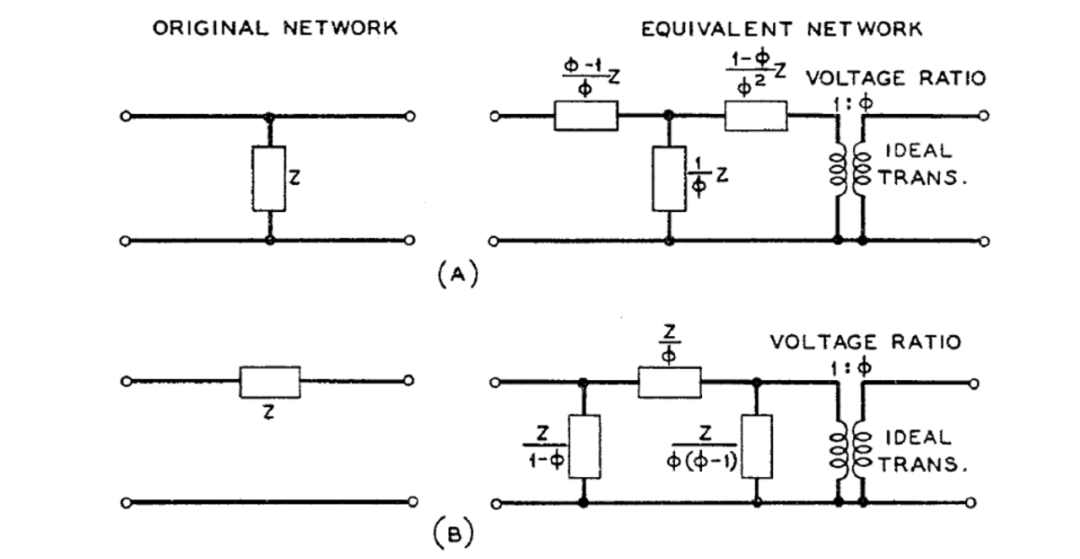
图15 表示阻抗变换原理的网络等效电路
图13的逆电路结构由并联谐振电路代替串联谐振电路组成,其设计方法完全相同,借助图15B所示的等效关系进行设计。
正元件的充分条件
从实际构造的角度来看,在实现物理梯形网络中的负元件时有时需要完全耦合的电感和理想变压器,这是非常不理想的。下面陈述的两个条件足以确保中间串联低通梯形网络中的所有元件都是正的,使得在梯形网络本身或与梯形网络通过频率变换或反演关系(如式(37))相关联的其他网络中,不需要使用耦合线圈或理想变压器。虽然这些条件不是必需的,但它们在证明滤波器设计中遇到的大多数梯形网络都期望在不使用耦合的情况下实现时非常有用。
假设一个中间串联低通电路结构和适当一般形式的阻抗,第一个条件要求所有无穷损耗的频率都是实数(或无穷大),并且大于至少一个开路驱动点阻抗的所有有限极点。第二个条件要求与最接近终端的并联分支的谐振相对应的特定无穷损耗频率也等于或大于相应开路阻抗的所有根。通过检查表I的公式并回顾所有的和都是正的,很容易建立这些条件的充分性。
一个有趣的特殊情况是所有的无穷损耗频率都出现在无穷远处。可以看出,上述条件在这个特殊情况下总是满足的。因此,所有形如式(35)且所有的都为零的功率比都可以用与定-k低通镜像参数滤波器相同电路结构的网络来实现,前提是满足一般物理要求,即它在所有实频率下必须不小于。对于所有的都为零的功率比(36),情况也是如此,相应的定-k电路结构仅包括奇数个“半段”。这两个特殊的功率比包括中的所有偶次多项式,它们具有单位常数项,并且满足实频率下的物理极限。
对称和逆阻抗梯形网络
用作滤波器的梯形网络通常具有满足两个特殊条件之一的阻抗和终端。一种条件要求电对称网络和相等的终端。另一个要求每个开路阻抗相对于终端的平均值等于网络另一端短路阻抗的倒数。
如果要满足对称性或逆阻抗的要求,在第一部分中,与插入损耗相关的阻抗公式(18)中的多项式或必须恒等于零。对和与插入功率比的关系的检查表明,它们的抵消需要以下形式的表达式:
在对称网络和相等终端的情况下,以及
在逆阻抗网络的情况下。
功率比的(38)和(39)形式的指标简化了设计方法,因为在确定和时不需要提取根,唯一的根提取涉及找到多项式和。很容易证明,这些功率比物理实现所需的条件允许和是的任何具有实系数的偶次多项式。换句话说,对于一般形式的每个功率比
至少有一个对应的对称或逆阻抗网络,其中是的任何具有实系数的奇或偶有理函数,而代表,并且当为奇函数时,它必须为1。
当的所有极点都是实数或虚数且有限时,导致对称网络的功率比(38)可以用适用于图9所示的正常电路结构中的中间串联低通梯形的形式(35)来表示。当遵守相同的条件,除了一个在无穷远处的项的单极点,并且当还选择和使得在零频率时为零时,导致逆阻抗网络的功率比(39)可以用适用于图11所示的在一端以并联电容终端的中间串联低通梯形的形式(36)来表示。对于非中间串联低通电路结构的梯形网络,存在完全相似的关系。
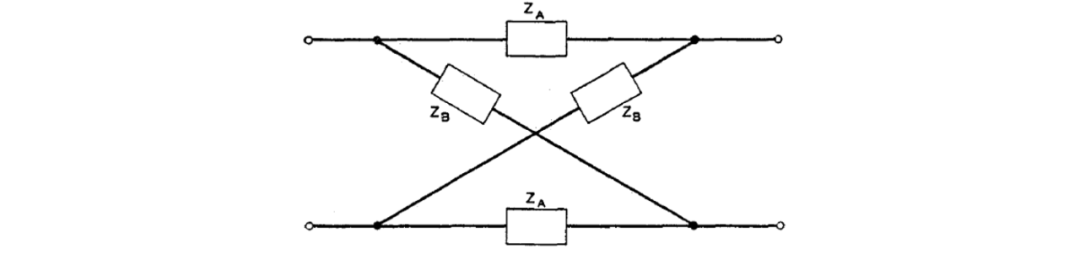
图16 平衡格型电路网络结构
格型网络与对称梯形网络的设计
众所周知,对于每一个电气上对称的实际网络,都存在一个如图16所示的等效格型网络。当开路和短路阻抗已知时,可以通过公知的公式非常容易地计算出阻抗臂。然而,当需要设计一个LC格型网络以产生形式为(38)规定的功率比时,通过下面描述的公式确定阻抗支路比先计算开路和短路阻抗,然后再计算阻抗臂的方式更简单。
当功率比以形式(38)给定时,值显然可以表示为的两个多项式的乘积:
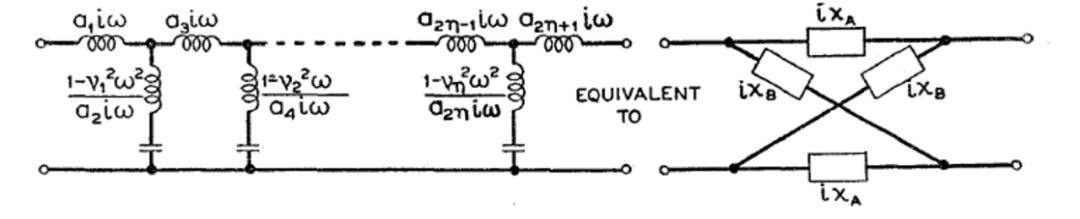
表II 中间串联梯形低通网络与格型网络等效
一级
两级
三级
其中都是偶次多项式,使得的所有根都是的具有负实部的根。结果表明,产生规定功率比的一个格型网络的阻抗臂和与等的关系由以下公式给出:
其中表示相等的终端电阻。获得与规定的功率比对应的其他三个LC格型网络,可以通过交换这些阻抗并用它们相对于的倒数来替换它们来实现。
在设计具有规定插入损耗的对称梯形电路时,通常从等效格型网络确定元件值比从开路和短路阻抗确定元件值更容易。例如,在设计一个、两个或三个并联支路的中间串联低通梯形电路或相关网络时,可以使用表II中列出的特殊设计公式。这些公式的推导方式与表I中的一般公式非常相似,通过使用开路阻抗来制定(30)中行列式的部分分式展开,并注意对称所需的常数之间的关系。常数之间的关系是由于开路阻抗与两个阻抗臂之和成正比,这要求相应部分分式的和在插损无限大的频率下相等。即使不使用其他特殊关系,将开路阻抗作为两个函数之和的初始确定也简化了使用表I所需的部分分式展开的计算。
脚注
[30]. 部分并不一定意味着具有镜像参数理论的属性的滤波器部分,而仅仅是当四端口网络串联连接时的组合的组成部分。
[31]. 互感的要求大大增加了构建网络的难度。如果需要线圈之间的理想耦合,它只能是近似的。如果要求低于理想耦合,则很难同时调整自感和互感。
[32]. 通过根据逆网络和频率变换的原理对C型和D型部分进行适当修改,可以获得由类似串联部分组成的其他规范网络。然而,在这里考虑上述串联组合的特殊类型就足够了。
[33]. 根据LC四端口的行列式及其各种余子式,输入阻抗为。除非在特殊情况下,相同因子的抵消导致阻抗函数的次数降低,这需要和与和成正比,其中和是阻抗函数的最简单有理分数表达式的分子和分母。行列式的必要偶性和奇性只允许对开路和短路阻抗有两个相应的解。事实证明,从一个解过渡到另一个解会改变的符号,因此只有一个解是物理的。
[34]. 函数的电阻部分定义为偶数部分,仅表示实频时的实部。
[35]. 更详细的设计方法将在后面进行说明。
[36]. 根据LC网络的行列式 及其各种余子式,输入阻抗的电阻部分表示为。显然,分母的单根只有在具有特殊值时才能与分子的任何双根重合。
[37]. 由于阻抗函数通常必须小于电路结构的常规次数,因此通常存在等效的2极,代表更有效地使用元件。尽管存在这种实际缺点,但了解这种特殊2极的规范性质对于一般网络理论问题是有用的。
[38]. 具体来说,损耗可以借助第一部分的(16)进行计算。
[39]. 在设计的每个阶段减少终止阻抗次数的精确方式是导致原始输入阻抗为正常次数的最终电路结构的原因。
[40]. 从输入阻抗计算终止阻抗可以消除阻抗部分的一对相同根,从而降低阻抗函数的次数,并且可以将一对或多对相同的实根转换为阻抗函数的根或极,或者反之亦然。否则,阻力部分的根保持不变。
[41]. 如前所述,第一部分的理论可用于证明任何正实函数都可以实现为电阻终止LC四端口的输入阻抗。
[42]. 网络的无限损耗频率是指通过一般有限电阻终端获得的无限损耗频率,不包括将插入电压比的一般表达式的根和极重合的任何特定终端。每个无限损耗频率都包含在以下一组或多组临界频率中:开路传输阻抗的根,短路传输阻抗的极,网络同一端的开路和短路驱动点阻抗的重合根或极,以及通过电阻终端获得的输入阻抗的电阻部分的零点。
[43]. 在许多情况下,可以消除负电感而无需引入耦合,但是这样做的条件并不简单。
[44]. 这种类型的梯形显然等效于通常与由一个或多个由简单串联电感组成的A型部分结合使用的C型部分。
[45]. 诺顿(Norton)引入了这些关系作为他的设计方程的基础。
[46]. 在当前的假设下,无限损耗的有限频率是开路传输阻抗的根,也是相应短路阻抗的有限极。
[47]. 这似乎与众所周知的事实相反,即需要三个阻抗才能确定一个四端口网络。这里提供的其他数据是通过假设适用于受特殊限制的特定电路结构的阻抗来提供的。回想一下,除了网络远端的两端并联支路外,还可以根据一个短路驱动点阻抗和短路传输阻抗来设计考尔(Cauer)的并联或导纳型规范LC四端口。对于正在考虑的特定电路,在等效并联类型规范网络中不存在终端并联支路,而可以从短路驱动点阻抗和无限损耗频率中找到短路传输阻抗。
[48]. 尽管变量在第一部分的一般理论中更方便,但事实证明在本文考虑的梯形网络理论中更方便。
[49]. 当稍后允许无限损耗点变为无限时,无限损耗点的值的倒数比其值本身更方便。
[50]. 例如,Fry(12)描述的各种梯形对应于Stieltjes分数。
[51]. 的公式涉及。如(27)、(28)和(29)所定义,这些量看起来很奇怪,因为它们只是一阶行列式。然而,这些一阶行列式仅代表。
[52]. 如果对应于短路阻抗,可以假设在短路处连接了一个任意的并联支路,因为它不会影响。这允许被准确地确定,就好像有一个完整的额外“部分”一样。
[53]. 这个推导还没有得到严格的证明,但已经进行得足够远,可以指出公式转换的方式。
[54]. 例如,参见Scott和Mathews(13)的论文中关于功能行列式的章节。
[55]. 和类型的高阶行列式的类似消失显示了连分数的有限性质(25)。
[56]. 离散选择常数意味着总是可以通过单个常数的微小变化来避免的选择。当然,假设满足物理要求,即它必须是正的,并且在所有实际频率下都不小于。
[57]. 如果允许修改中间串联的低通梯形网络,实际上所有解通常都是可实现的。例如,如果网络的一端包含理想变压器,则可以违反对或符号的要求。同样,如果向梯形的一端添加并联电容器,并且允许用完全耦合的线圈实现负串联电感,则可以正常违反对符号的要求。
[58]. 当然也可能是负的,导致负元件,但这些都可以通过耦合线圈来实现。
[59]. 然而,与谐振并联支路相邻的终端串联电感的消失通常不会以这种方式改变功率比表达式中分子的次数。
[60]. 当然,在频率变换中包含任意常数因子有时更方便。例如,在带通滤波器的设计中,通常方便的是首先设计一个截止频率为的低通滤波器。然后,通过用代替来获得所需的带通滤波器,代表
其中对应于带通滤波器的两个截止频率。
[61]. 除了一个或多个并联支路是简单电感的限制情况外,这种类型的等效总是存在的。通过用电容代替电感,反之亦然,总是可以得到类似的等效电路结构,除非一个或多个并联支路是简单的电容器。当遇到简单的电感和电容并联支路时,必须使用特殊的设计方法。
[62]. Norton(14)发现了由图15A和15B表示的阻抗变换原理。在确定图13所示的网络电路结构与图14所示的类型之一时,串联电容如何在不同的串联支路之间分配存在相当大的任意性。
[63]. 除非它们被修改以补偿耗散效应。
[64]. 如果在网络描述中使用像阻抗和传输常数,则这些条件分别要求相等和反向的像阻抗。
[65]. 当为奇数且不等于1时,开路驱动点阻抗的比值,与相应短路阻抗的比值相同,将等于终端的比值。这允许使用对称网络与理想变压器的组合。在反向阻抗网络的情况下允许不等终端是方便的,而在对称或比例阻抗的情况下则不方便,因为在反向阻抗的情况下,如果要避免理想变压器,通常需要不等终端。
[66]. Campbell(15)指出了这一点。
[67]. 就形式(38)的功率比而言,多项式和有些任意。然而,结果表明,尽管存在这种任意性,但只有四个相应的格型网络。
参考文献
1). Pupin, M. I.: "Wave Propagation over Non-Uniform Cables and Long Distance Air-Lines," Trans. A. I. E. E., 17, 445-507 (1900).
2). Campbell, G. A.: "On Loaded Lines in Telephonic Transmission," Phil. Mag., 5, 313-330 (1903).
3). Zobel, O. J.: "Theory and Design of Uniform and Composite Electric Wave Filters," Bell System Tech. Journal, 2, 1-46 (1923), and "Transmission Characteristics of Electric Wave Filters," Bell System Tech. Journal, 3, 567-620 (1924).
4). Bode, H. W.: "A General Theory of Electric Wave Filters," Journal of Math. and Physics, 13, 275-362 (1934).
5). Cauer, W.: "Ein Reaktanztheorem," Preuss. Akad. d. Wissenschaften, Phys.Math. Kl., Sitzber., Nos. 30-32, 673-681 (1931).
6). Gewertz, C. M.: "Synthesis of a Finite Four-Terminal Network from its Prescribed Driving-Point Functions and Transfer Function," Journal of Math. and Physics, 12, 1-257 (1933).
7). Norton, E. L.: "Constant Resistance Networks with Applications to Filter Groups," Bell System Tech. Journal, 16, 178-193 (April, 1937).
8). Brune, O.: "Synthesis of a Finite Two-Terminal Network Whose DrivingPoint Impedance is a Prescribed Function of Frequency," Journal of Math. and Physics., 10, 191-235 (1931).
9). Dietzold, R. L.: "A Mechanical Root Finder," Bell Labs. Record, 16, Dec., 1937.
10). Mayer, H. F.: "Ueber die Daempfung von Siebketten in Durchlaissigkeitsbereich," E. N. T., 2, 335-338 (1925).
11). Bode, H. W. and Dietzold, R. L.: "Ideal Wave Filters," Bell System Tech. Journal, 14, 215-252 (1935).
12). Fry, T. C.: "The Use of Continued Fractions in the Design of Electrical Networks," Am. Math. Soc., Bull., 35, 463-498 (1929).
13). Scott, R. F. and Mathews, G. B.: "The Theory of Determinants," Second Edition, 1904.
14). Norton, E. L.: U. S. Patent No. 1681554.
15). Campbell, G. A.: "Physical Theory of the Electric Wave-Filter," Bell System Tech. Journal, 1, 1-32 (1922).
16). Cauer, W.: "Ein Interpolationsproblem mit Funktionen mit Positiven Realteil," Mathematische Zeitschrift, 38, 1-44 (1933).
17). Shea, T. E.: "Transmission Networks and Wave Filters," D. Van Nostrand Co., New York, 1929 -p. 253, Fig. 138.
18). Guillemin, E. A.: "Communication Networks," John Wiley and Sons, New York, N. Y., 1935-Vol. II.
19). Cayley, A.: "An Elementary Treatise on Elliptic Functions," second edition, G. Bell and Sons, London, 1895.
20). Jacobi, C. G. J.: "Fundamenta Nova Theoriae Functionum Ellipticarum," Königsberg, 1829.
21). Silberstein, L.: "Synopsis of Applicable Mathematics," G. Bell and Sons, London, 1923-Section on Elliptic Functions, pp. 152-170.
22). Bode, H. W.: U. S. Patents Nos. 1955788, 2002216, 2029014.
审核编辑:黄飞
 电子发烧友App
电子发烧友App






























评论