利用自适应子波变换提高对微弱运动目标的检测性能
本文研究了长时间相参积累时微弱运动目标回波信号的特点,分析了常规检测方法的局限性,针对多项式相位信号模型,结合复正交线性相位子波基函数的设计,提出了一种基于自适应子波变换局域线性逼近的微弱运动目标检测方法,该方法具有自适应频带划分,快速算法实现,计算量低,并对统计分布的杂散分量具有自动抑制的特点.理论分析和计算机仿真结果验证了该方法的有效性.
关键词:微弱信号检测;相参积累;AWT检测器
An Improved Coherent Integration Detector with Adaptive Wavelet Transform
WANG Jun,ZHANG Shou-hong,YANG Ke-hu
(Key Laboratory for Radar Signal Processing,Xidian University,Xi'an 710071,China)
Abstract:This paper proposes a novel long-term coherent integration method for detection of weak high order polynomial phase signal (PPS),such as weak echo signals from maneuvering targets in radar and sonar applications.The method exploits the time-frequency tiling property of adaptive wavelet transform (AWT),and is practically realzable.In this paper,the unitary and linear phase wavelet basis function together with one order local linear approaching procedure are presented to estimate the signal trace in time-frequency plane.Additionally,the Radon-Wigner transform (RWT) is exploited in subband outputs of AWT to achieve low computational complexity implementation.Analysis and simulation results confirm the efficacy of the method.
Key words:weak signal detection;long-term coherent integration;AWT detector
一、引 言
在雷达、声纳等探测系统中对微弱运动目标的检测一直是比较困难的,主要原因是这类目标的回波强度小且多普勒频率变化复杂.为了检测强背景中的运动目标,除了常规杂波抑制、抗干扰和降低系统噪声等措施外,一种比较有效的方法是利用相参积累技术来增强接收回波,即用时间换取能量.一般而言相参积累时间受目标穿越波束和回波包络移动等因素的影响,而积累的性能主要取决于目标回波的相干性.通常,若目标作机动飞行,则随波束驻留时间的增加,则目标回波相干性变差,此时传统的谱分析方法是失效的.为此人们提出了基于线性调频回波模型的各种检测方法[1,2],并建立了快速算法[3].实际上,在相对较长的一段观测时间内由于目标的复杂运动而产生的回波信号已不能用线性调频模型去近似.因此,有必要研究在这种情况下的信号检测问题.本文基于推广的多项式相位回波模型,提出了利用自适应子波变换作线性逼近对目标回波信号进行长时间相参积累的检测方法.由于回波信号的频率变化呈现非线性特征,不同的时间上多普勒变化特征不同,利用自适应子波划分,可以将信号全局多普勒变化转化为局域线性逼近,从而以区间时变的多普勒相参技术取代常规线性调频模型下的RWT技术.另外AWT方法存在快速变换,其分岔树结构易于实现,对回波的局域优化分割还有助于包络补偿的实现,同时,多尺度多分辨性能使得AWT保持着对统计分布型杂散分量的自动抑制能力,结合子带信号能量的RWT技术,可以在不增加太多运算量的同时,得到对微弱运动目标良好的相参积累检测性能.
二、长相参积累时目标回波的相干性
为了检测隐身等微弱运动目标信号,可以采用稀布阵综合脉冲孔径雷达的波束驻留工作方式或让常规雷达工作在“烧穿”方式下,以增加回波脉冲数.已知运动目标回波信号的多普勒频率为
fd=(2V/λ)cosφ(t) (1)
其中λ为雷达波长,V为目标的运动速度,φ(t)为目标运动方向与雷达视线的夹角.常规波束扫描雷达在一次扫描中接收到的脉冲数由于受天线扫描的影响而较少,对这些回波,可以认为其fd是不变的.但是在固定波束照射下,由于观测时间的增加,即使对匀速直线运动的目标,由于φ(t)的变化而产生的多普勒频率的变化已不能忽略,其大小为
Δfd=(4V/λ)sin(θb/2)sinφ0 (2)
式中θb为天线波束宽度,φ0为目标匀速运动方向与波束轴线的夹角.式(2)仅仅假设目标为匀速运动的情况,实际上,在数秒的相参时间内,目标的运动情况可能包括加减速及机动拐弯等复杂运动.若目标作匀加速运动(机动拐弯的情况类似),即V(t)=V0+at,a为瞬时加速度,可以导出其fd的变化率为:
(3)
其中R为目标距离.由于在回波相参时间内,φ(t)∈[0,θb],且R很大,上式中忽略了(1/R)的高次项的影响.式(3)表明由于目标相对雷达视角作匀加速机动而导致μf为高阶时变的函数.因此,为了分辨高阶时变相位引入的非线性频率调制,充分利用目标相干性,则需要引入频率局域分辨的思想,而利用传统方法实现对非线性调频信号和相参积累,实质是一种全域分辨,得不到应有的频率分辨力.
三、复对称正交子波基的设计
由于不同子波基函数的分辨性能不同,选择有良好局域性能的子波基是重要的.为了有利于长时间雷达相参回波的积累,我们希望子波基函数具有线性相位、有限冲激响应、正交分解的特点并存在快速变换实现.
从Daubechies的FIR滤波器设计可知,其尺度函数满足①紧支性,②正交性的约束关系.因此,只要能找到一个合适的尺度函数,在一定准则的约束下,就能得到信号在多分辨空间的逼近,从而构造出相应的正交子波分解.Mallat给出了下面的关系,使得我们能够利用滤波器组来产生相应的尺度和子波函数.
若设为由ck定义的离散滤波器的传递函数,则正交条件可表示为|H0(ω)|2+|H0(ω+π)|2=1,且|H0(0)|=1.若ck,k=1,…,N且|H0(ω)|≠0,则
(4)
其中,H1(ω)=e-jω0(ω+π),“-”表示复共轭.并不是具有任意冲缴响应的滤波器都可以用来产生子波,一般要求H0(ω)应是一半带低通滤波器,则H0(z)在z=-1处至少应有一个零点存在.若H0(z)可以分解为下列形式:
(5)
且满足(1)F(0)=1,(2)B=sup|F(ejω)|,则Daubechies证明了若B<2N-1,则由式(5)能够生成紧支连续可导的尺度和子波函数.
另外,为使子波函数具有较好的频率分辨力,应使其满足一定的正则性要求,即
(6)
Daubechies子波皆为满足上述条件的实多项式的解,但不具备线性或广义线性相位特性,这样在处理中不可避免地带来了新的相位分量,从而影响子带信号的相参积累.
为了构造线性相位或零相位复值正交子波变换,Lawton考虑了对称性条件[4],并由此得到了一定条件下(如N为偶数)时的复值子波系数.这里通过定义一种满足式(5),(6)以及Daubechies收敛条件的有效多项式,来获得一般条件下复对称正交子波函数的构造.可以证明,常规的实对称Haar子波,Daubiechies子波及Lawton复值子波函数,均是该多项式生成子波函数的特殊情况.定义:
P(z)=((1+z)/2)2N+2PN(z-1) (7)
其中,且
(8)
多项式PN(z)的2J个根给出了不同的解,由此可生成不同的子波基.通过对PN(z)作因式分解,可得:
H0(z)=((1+z)/2)1+J.q(z-1) (9)
其中,xm和xm为PN(z)在单位圆内的根,n为xn的复共轭,R为{1,2,…,N}的任一子集,U′和U的补.利用式(7)~(9)生成的复值正交子波函数,具有最大平坦、有限冲激响应、线性相位及快速分解特性.
四、利用AWT改善长时间相参积累性能
利用线性调频模型的RWT变换实现积累,原理上看其时频是平稳相关,但由于目标具有时变非平稳特征,故需要进行联合时频域分辨.利用上节的复正交线性相位子波函数,可以用AWT把对高阶非线性多普勒变化用区间线性来近似.结合AWT的快速实现,这种逼近不需进行多维搜索而能自适应地分段匹配于信号.而且,不同子带上频率变化有相关性,无需作全程优化,据此可进一步降低算法的计算量,得到较好的检测性能.
1.回波信号的自适应子波变换
设{x(n),n=1,2,…,N}是不同观测期内的回波信号,N为可能收到的总回波数.对于自适应子波的局域划分,对每个分岔树上的信号,可描述为:
(10)
式中Wj,m(n)为第j个分解层上,m个子带中第n个子波系数,Wj+1,2m(n)和Wj+1,2m+1(n)为Wj,m(n)的一个二叉树,h(n)为酉尺度滤波器,g(n)为酉子波滤波器.快速离散自适应子波分解可通过塔形算法实现.复正交滤波器分解特性使得Wj,m(n)满足能量守恒关系,即用任意的时频瓦片划分结构覆盖全频率段,不同的瓦片间能量无冗余结构.这种分解有助于获得优化的局域匹配效果.
最佳子集的获取与代价函数有关,通常可采用的代价函数有多种,如门限法、最小lp范数法、最小方差和熵函数法等.其中最小熵意味着在一定的均方误差条件下提取通带信号能量的最集中表示.由于统计分布的杂散分量其熵函数较高,则最小熵准则使得杂噪分量散布,利于子带的局域相参积累和检测处理.
2.AWT长时相干积累检测方法
设回波信号模型由如下P阶多项式相位信号表示,即x(t)=A.ej2πφ(t),其中,则检测问题表示为:
Hm:r(t)=m.x(t)+n(t),m=0,1 (11)
这里r(t)为观测信号,t∈[-Tc/2,Tc/2].设n(t)为独立随机复高斯噪声,Ω={P,ai,i=1,…,P}为信号参数空间.利用广义最大似然估计可得到上述检测问题的检测统计量为
(12)
式中和i是Ω的最大似然估计.式(12)实现的最优解实际上是对回波非线性频率变化的瞬时相位补偿,因而能获得检测的性能上限.然而,最大似然估计是对Ω的(P+1)维联合寻优问题,具有很大运算量,很难具体实现,而利用AWT多分辨,实质上把最大似然估计对信号参数Ω的多维联合搜索简化为多个相关的一维搜索,同时保持检测器性能基本不变,它是一种次最优的实现方案.AWT长时间相干积累检测器的检测统计量为:
(13)
|
图1 检测算法流程图 其中M为优化的时频单元划分数目,μj,m为一阶逼近斜率,F(.)表示傅里叶变换.利用AWT法实现长时间相干积累的特点在于它将长时间的多普勒频率的非线性变化分割为局域线性特征,由于对线性调频信号的检测方法比较成熟,又有基于Radnon-Wigner变换的解线性调频的快速算法存在,所以利用AWT法对回波能量的利用率理论上只取决于局域时频分割的大小,时频单元划分越细,对频率的分辨越高,能量利用率越高.但是过细的划分是不必要的.我们知道通常情况下,目标机动而引起的多项式相位的阶数不会太高,即非线性频率变化是有限阶可导的连续函数.为了避免增加运算量,原则上在性能损失不大的情况下(即近似线性),则应选择最少的时频单元划分数目. (14) 对于RWT检测器,其输出检测量为: (15) 一般对上式中的积分不可能得出一个闭合形式的解,但是,利用积分的渐近矩展开式[5],我们可以推出它的一个近似解为: (16) 上式表明,对式(14)的信号用RWT方法作相参积累,其性能受到非线性相位项的制约,如果这种非线性相位项的阶数越高,调制指数越大,则性能下降得越多.而利用前述AWT的优化分段线性逼近方法,理想情况下,就是对时频曲线实现相参积分,此时相当于对式(14)中的高阶多项式瞬时相位进行正确补偿后的积累输出,即令a1,a2→0时的结果: (17) 这里X(f)为x(t)的傅氏变换.因此,AWT检测器相对于RWT检测器对有限长非线性调频回波信号的理想积累改善因子为: (18) 式(18)表明,积累改善的程度与可积累时间成正比,与非线性调频参数的大小成正比.其物理意义也很明确,若目标机动性越强,则调频曲线越弯曲,利用AWT方法所带来的检测增益也就越大. 五、仿真结果 |
|
图2 目标单元的时频特性(SNR=-3dB) |
|
图3(a) 常规方法 |
|
图3(b) RWT检测器输出 |
|
图3(c) AWT检测器输出 |
|
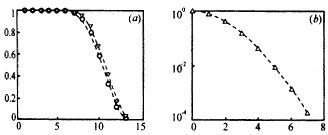
图4 检测性能(□:AWT,◆:RWT,◇:常规方法) 六、结 论 |
 电子发烧友App
电子发烧友App






















评论